Giải Toán 9 trang 66 tập 1 Chân trời sáng tạo

Giải Toán 9 trang 66 Tập 1 Chân trời

Bài 1 Trang 66 Toán 9 tập 1 Chân trời
Bài 2 Trang 66 Toán 9 tập 1 Chân trời
Bài 3 Trang 66 Toán 9 tập 1 Chân trời
Bài 4 Trang 66 Toán 9 tập 1 Chân trời
Bài 5 Trang 66 Toán 9 tập 1 Chân trời
Bài 6 Trang 66 Toán 9 tập 1 Chân trời
Bài 7 Trang 66 Toán 9 tập 1 Chân trời

Giải Toán 9 trang 66 Tập 1 CTST hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Chân trời sáng tạo tập 1 trang 66.

Bài 1 Trang 66 Toán 9 tập 1 Chân trời

Cho tam giác ABC vuông tại A. Tính các tỉ số lượng giác của góc B trong mỗi trường hợp sau:

a) BC = 5 cm; AB = 3 cm

b) BC = 13 cm; AC = 12 cm

c) $BC = 5\sqrt{2}$ $B C = 5 \sqrt{2}$ cm; AB = 5 cm

d) $AB=a\sqrt{3}$ $A B = a \sqrt{3}$ ; AC = a.

Hướng dẫn giải:

Xét tam giác ABC vuông tại A:

a) Ta có: AC² = BC² - AB² = 5² - 3² = 16

Suy ra AC = 4 cm

$\sin B=\frac{AC}{BC}=\frac{4}{5}$ $\sin B = \frac{A C}{B C} = \frac{4}{5}$

$\tan B=\frac{AC}{AB}=\frac{4}{3}$ $\tan B = \frac{A C}{A B} = \frac{4}{3}$

$\cos B=\frac{AB}{BC}=\frac{3}{5}$ $\cos B = \frac{A B}{B C} = \frac{3}{5}$

$\cot B=\frac{AB}{AC}=\frac{3}{4}$ $\cot B = \frac{A B}{A C} = \frac{3}{4}$

b) Ta có: AB² = BC² - AC² = 13² - 12² = 25

Suy ra AB = 5

$\sin B=\frac{AC}{BC}=\frac{12}{13}$ $\sin B = \frac{A C}{B C} = \frac{12}{13}$

$\tan B=\frac{AC}{AB}=\frac{12}{5}$ $\tan B = \frac{A C}{A B} = \frac{12}{5}$

$\cos B=\frac{AB}{BC}=\frac{5}{13}$ $\cos B = \frac{A B}{B C} = \frac{5}{13}$

$\cot B=\frac{AB}{AC}=\frac{5}{12}$ $\cot B = \frac{A B}{A C} = \frac{5}{12}$

Bài 2 Trang 66 Toán 9 tập 1 Chân trời

Tính giá trị của các biểu thức sau:

a) $A=\frac{\sin30^{\circ} \ .\ \cos30^{\circ} }{\cot45^{\circ} }$ $A = \frac{\sin 30^{\circ} . \cos 30^{\circ}}{\cot 45^{\circ}}$

b) $B=\frac{\tan30^{\circ} }{ \cos45^{\circ}.\cos60^{\circ} }$ $B = \frac{\tan 30^{\circ}}{\cos 45^{\circ} . \cos 60^{\circ}}$

Hướng dẫn giải:

a) $A=\frac{\sin30^{\circ} \ .\ \cos30^{\circ} }{\cot45^{\circ} }$ $A = \frac{\sin 30^{\circ} . \cos 30^{\circ}}{\cot 45^{\circ}}$

$=\frac{\frac{1}{2} \ .\ \frac{\sqrt{3} }{2} }{1 } =\frac{\sqrt{3} }{4}$ $= \frac{\frac{1}{2} . \frac{\sqrt{3}}{2}}{1} = \frac{\sqrt{3}}{4}$

b) $B=\frac{\tan30^{\circ} }{ \cos45^{\circ}.\cos60^{\circ} }$ $B = \frac{\tan 30^{\circ}}{\cos 45^{\circ} . \cos 60^{\circ}}$

$=\frac{\frac{\sqrt{3} }{3} }{ \frac{\sqrt{2} }{2}.\frac{1 }{2} } =\frac{2\sqrt{6} }{3}$ $= \frac{\frac{\sqrt{3}}{3}}{\frac{\sqrt{2}}{2} . \frac{1}{2}} = \frac{2 \sqrt{6}}{3}$

Bài 3 Trang 66 Toán 9 tập 1 Chân trời

Hãy viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn 45^o:

a) sin 60^o

b) cos 75^o

c) tan 80^o

Hướng dẫn giải:

a) sin 60^o = cos (90^o - 60^o) = cos 30^o

b) cos 75^o = sin (90^o - 75^o) = sin 15^o

c) tan 80^o = cot (90^o - 80^o) = cot 10^o

Bài 4 Trang 66 Toán 9 tập 1 Chân trời

Sử dụng máy tính cầm tay, tính tỉ số lượng giác của các góc sau:

a) 26^o

b) 72^o

c) 81^o27'

Hướng dẫn giải:

a) Ta có: sin 26^o ≈ 0,44; cos 26^o ≈ 0,90

tan 26^o ≈ 0,49; cot 26^o ≈ 2,05

b) Ta có: sin 72^o ≈ 0,95; cos 72^o ≈ 0,31

tan 72^o ≈ 3,08; cot 72^o ≈ 0,32

c) Ta có: sin 81^o27' ≈ 0,99

cos 81^o27' ≈ 0,15

tan 81^o27' ≈ 6,65

cot 81^o27' ≈ 0,15.

Bài 5 Trang 66 Toán 9 tập 1 Chân trời

Sử dụng máy tính cầm tay, tính tỉ số lượng giác của các góc sau:

a) cos α = 0,6

b) tan α = 34

Hướng dẫn giải:

a) cos α = 0,6 ⇒ α ≈ 53^o 7'

b) tan α = 34 ⇒ α ≈ 36^o52'

Bài 6 Trang 66 Toán 9 tập 1 Chân trời

Tia nắng chiếu qua nóc của một tòa nhà hợp với mặt đất một góc α. Cho biết tòa nhà cao 21 m và bóng của nó trên mặt đất dài 15 m (Hình 10). Tính góc α (kết quả làm tròn đến độ).

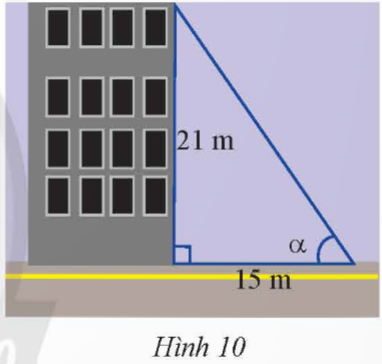
Hướng dẫn giải:

Bài 7 Trang 66 Toán 9 tập 1 Chân trời

Một cái thang 12 m được đặt vào một bức tường sao cho chân thang cách tường 7 m (Hình 11). Tính góc α tạo bởi thang và tường.

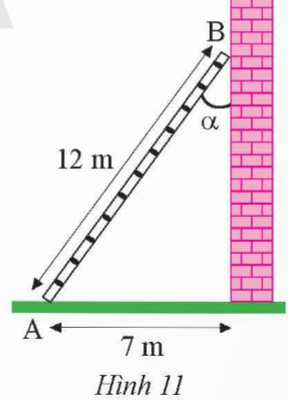
Hướng dẫn giải:

----------------------------------------------

---> Xem thêm: Giải Toán 9 trang 67 tập 1 Chân trời sáng tạo

Lời giải Toán 9 trang 66 Tập 1 Chân trời sáng tạo với các câu hỏi nằm trong Bài 1: Tỉ số lượng giác của góc nhọn , được VnDoc biên soạn và đăng tải!

Xem thêm các bài Tìm bài trong mục này khác:

Chia sẻ, đánh giá bài viết

1

550

Bài trước

Bài sau

Chia sẻ bởi:
Lê Jelar

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

Tải tài liệu Trả phí + Miễn phí

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!