Toán 9 Chân trời sáng tạo Bài 1: Hàm số và đồ thị của hàm số y = ax^2 (a khác 0)
Toán 9 CTST bài 1
Giải Toán 9 Chân trời sáng tạo Bài 1: Hàm số và đồ thị của hàm số y = ax2 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Chân trời sáng tạo tập 2 trang 10, giúp các em nâng cao kỹ năng giải Toán lớp 9 sách mới.
Bài 1 trang 10 Toán 9 Tập 2
Cho hàm số y = - x2
a) Lập bảng giá trị của hàm số.
b) Vẽ đồ thị hàm số.
Hướng dẫn giải:
a) Ta có bảng giá trị:
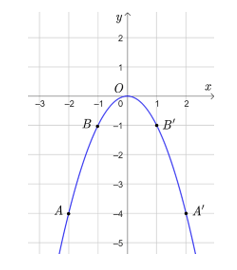
Trên mặt phẳng tọa độ, lấy các điểm A(−2; −4), B(−1; −1), O(0; 0), B'(1; −1), A'(2; −4).
Đồ thị hàm số y = −x2 là một đường parabol đỉnh O, đi qua các điểm trên và có dạng như dưới đây.
Bài 2 trang 10 Toán 9 Tập 2
Cho hàm số 
\(y = \frac{1}{2}{x^2}\)
a) Vẽ đồ thị hàm số.
b) Trong các điểm A(-6;-8), B(6;8), \(C \left( {\frac{2}{3};\frac{2}{9}} \right)\), điểm nào thuộc đồ thị của hàm số trên?
Hướng dẫn giải:
a) Bảng giá trị:
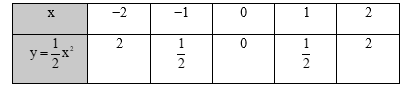
Trên mặt phẳng tọa độ, lấy các điểm A\((-2;2), B(-1; \frac{1}{2}), O(0;0), B’(1; \frac{1}{2}), A’(2;2)\)
Đồ thị hàm số \(y = \frac{1}{2}{x^2}\) là một đường parabol đỉnh O, đi qua các điểm trên và có dạng như dưới đây.
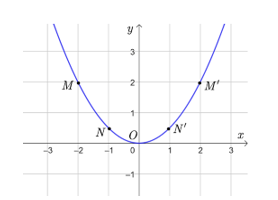
b) Thay A(-6;-8) vào \(y = \frac{1}{2}{x^2}\),ta có: \(-8 \ne 18\) nên A(-6;-8) không thuộc đồ thị hàm số.
Thay B(6;8) vào \(y = \frac{1}{2}{x^2}\) ,ta có: \(8 \ne 18\) nên B(6;8) không thuộc đồ thị hàm số.
Thay \(C \left( {\frac{2}{3};\frac{2}{9}} \right)\) vào \(y = \frac{1}{2}x2\) ,ta có: \(\frac{2}{9} = \frac{2}{9}\) nên \(C \left( {\frac{2}{3};\frac{2}{9}} \right)\) thuộc đồ thị hàm số.
Bài 3 trang 10 Toán 9 Tập 2
Cho hai hàm số \(y = \frac{1}{4}{x^2}\)và \(y = - \frac{1}{4}{x^2}\). Vẽ đồ thị của hai hàm số đã cho trên cùng một mặt phẳng tọa độ Oxy.
Hướng dẫn giải:
Bảng giá trị của hàm số:
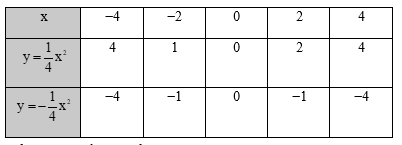
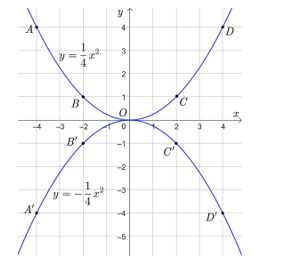
Trên mặt phẳng tọa độ, lấy các điểm A(-4;4), B(-2; 1), O(0;0), C(2; 1), D(4;4)
A’(-4;-4), B’(-2; -1), C’(2; -1), D’(4;-4)
Đồ thị hàm số \(y = \frac{1}{4}{x^2}\)là một đường parabol đỉnh O, đi qua các điểm A(-4;4), B(-2; 1), O(0;0), C(2; 1), D(4;4) và có dạng như dưới.
Đồ thị hàm số \(y = - \frac{1}{4}{x^2}\)là một đường parabol đỉnh O, đi qua các điểm A’(-4;-4), B’(-2; -1), O(0;0), C’(2; -1), D’(4;-4) và có dạng như dưới.
Bài 4 trang 10 Toán 9 Tập 2:
Cho hàm số y = ax2 (a ≠ 0).
a) Tìm a, biết đồ thị của hàm số đi qua điểm M(2; 6).
b) Vẽ đồ thị của hàm số với a vừa tìm được.
c) Tìm các điểm thuộc đồ thị của hàm số có tung độ y = 9.
Bài 6 trang 10 Toán 9 Tập 2:
Khi gió thổi vuông góc vào cánh buồm của một con thuyền thì lực F (N) của nó tỉ lệ thuận với bình phương tốc độ v (m/s) của gió, tức là F = av2 (a là hằng số). Biết rằng khi tốc độ của gió bằng 3 m/s thì lực tác động lên cánh buồm bằng 180 N.
a) Tính hằng số a.
b) Với a vừa tìm được, tính lực F khi v = 15 m/s và khi v = 26 m/s.
c) Biết rằng cánh buồm chỉ có thể chịu được một lực tối đa là 14 580 N, hỏi con thuyền có thể đi được trong gió bão với tốc độ gió 90 km/h hay không?
Hướng dẫn giải
a) Thay v = 3, F = 180 vào F = av2, ta được:
180 = a.32 suy ra a = 20.
b) Ta có a = 20 nên có công thức F = 20v2, thay v = 15 m/s ta được:
F = 20 . 152 = 4500 (N).
Thay v = 26 m/s ta được F = 20.262 = 13 520 (N).
c) Đổi 90 km/h = 25 m/s.
Thay F = 14 580 vào F = 20v2 (v > 0), ta có:
14 580 = 20v2
v2 = 729
v = 27 (thỏa mãn) hoặc v = −27 (loại).
Vậy con thuyền có thể đi được trong gió bão với tốc độ gió tối đa là 27 m/s nên có thể đi với tốc độ gió 25 m/s hay 90 km/h.
