Giải Toán 9 trang 101 tập 1 Chân trời sáng tạo
Giải Toán 9 trang 101 Tập 1 Chân trời
Giải Toán 9 trang 101 Tập 1 CTST hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Chân trời sáng tạo tập 1 trang 101.
Hoạt động 3 Trang 101 Toán 9 tập 1 Chân trời
a) Vẽ đường tròn (C) tâm O bán kính r = 5 cm và đường tròn (C') tâm O bán kính R = 8 cm
b) Tính diện tích S của (C) và diện tích S' của (C')
c) Hãy cho biết hiệu số (S' – S) biểu diễn diện tích của phần nào trên Hình 9.
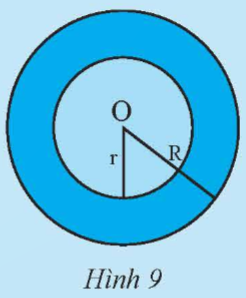
Hướng dẫn giải:
b) Diện tích S của đường tròn (C) là:
S = π . 52 = 25π ≈ 78,54 (cm2)
Diện tích S' của đường tròn (C') là:
S' = π . 82 = 64π ≈ 201,06 (cm2)
c) Hiệu số (S' – S) biểu diễn diện tích phần màu xanh đậm (phần được giới hạn bởi hai đường tròn (C) và (C'))
Thực hành 3 Trang 101 Toán 9 tập 1 Chân trời
Tính diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; 10 cm) và (O; 20 cm) (kết quả làm tròn đến hàng phần trăm).
Hướng dẫn giải:
Diện tích hình vành khuyên giới hạn bởi đường tròn (O; 10 cm) và (O; 20 cm) là:
S = π(R2 – r2) = π . (202 – 102) ≈ 942,48 (cm2)
Vận dụng 3 Trang 101 Toán 9 tập 1 Chân trời
Cho hình vành khuyên giới hạn bởi hai đường tròn (O; r) và (O; R) với R > r. Trên đường tròn (O; R) lấy hai điểm B, C sao cho BC vừa là dây cung của (O; R), vừa là tiếp tuyến của đường tròn (O; r) tại A (Hình 11).
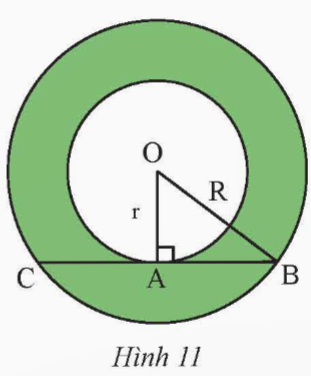
a) Tính độ dài đoạn thẳng BC theo r và R.
b) Cho 
\(BC=a\sqrt{3}\). Tính diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; r) và (O; R) theo a.
Hướng dẫn giải:
a) Ta có BC là tiếp tuyến của (O; r) tại tiếp điểm A nên OA ⊥ BC
Tam giác OBC cân tại O (OB = OC = R) có OA là đường cao
Do đó OA cũng là đường trung tuyến của BC hay AB = AC
Xét tam giác OAB vuông tại A, ta có:
OA2 + AB2 = OB2 (định lí Pythagor)
Suy ra AB2 = OB2 - OA2 = R2 - r2 hay \(AB=\sqrt{R^2-r^2}\)
Vậy \(BC=2AB=2\sqrt{R^2-r^2}\)
b) Diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; r) và (O; R) là:
\(S=\pi(R^2-r^2)=\pi.AB^2=\frac{\pi.BC^2}{4}=\frac{3\pi a^2}{4}\) (đvdt)
----------------------------------------------
---> Xem thêm: Giải Toán 9 trang 102 tập 1 Chân trời sáng tạo
Lời giải Toán 9 trang 101 Tập 1 Chân trời sáng tạo với các câu hỏi nằm trong Bài 4: Hình quạt tròn và hình vành khuyên, được VnDoc biên soạn và đăng tải!
