Giải Toán 9 trang 99 tập 1 Chân trời sáng tạo
Giải Toán 9 trang 99 Tập 1 Chân trời
Giải Toán 9 trang 99 Tập 1 CTST hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Chân trời sáng tạo tập 1 trang 99.
Thực hành 1 Trang 99 Toán 9 tập 1 Chân trời
Tính độ dài cung 72o của một đường tròn có bán kính 25 cm.
Hướng dẫn giải:
Cung 72o, bán kính R = 25 cm có độ dài là:
\(l=\frac{\pi Rn}{180}=\frac{\pi.25.72}{180}=10\pi\approx31,42\) cm
Vận dụng 1 Trang 99 Toán 9 tập 1 Chân trời
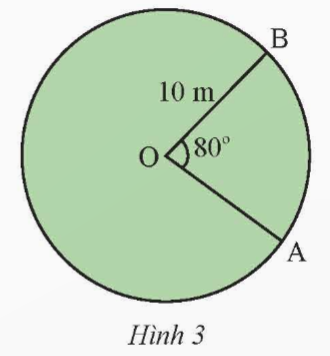
Tính độ dài của đoạn hàng rào từ A đến B của sân có trong Hình 3, cho biết \(\widehat{AOB}=80^{\circ}\)
Hướng dẫn giải:
Ta có \(\text{sđ }\overset \frown{AB} = \widehat{AOB}=80^{\circ}\)
Độ dài của đoạn hàng rào từ A đến B là:
\(l_{AB}=\frac{\pi Rn}{180}=\frac{\pi.10.80}{180}\approx13,96\) m
Hoạt động 2 Trang 99 Toán 9 tập 1 Chân trời
a) Ta có thể tính diện tích của miếng bánh pizza trong Hình 4a theo góc ở tâm và bán kính của ổ bánh hay không?
b) Chia một hình tròn bán kính R thành 360 phần bằng nhau.
i) Tính diện tích của mỗi phần đó.
ii) Tính diện tích phần hình tròn ghép bởi n phần bằng nhau nói trên (Hình 4b).
Hướng dẫn giải:
a) Có thể tính được diện tích của miếng bánh pizza theo góc ở tâm và bán kính của ổ bánh.
b) Diện tích của một hình tròn bán kính R là: πR2 (đvdt)
i) Diện tích mỗi phần là: \(\frac{πR^{2} }{360}\) (đvdt)
ii) Diện tích phần hình tròn ghép bởi n phần bằng nhau là:
\(\frac{n.πR^{2} }{360}\) (đvdt)
----------------------------------------------
---> Xem thêm: Giải Toán 9 trang 100 tập 1 Chân trời sáng tạo
Lời giải Toán 9 trang 99 Tập 1 Chân trời sáng tạo với các câu hỏi nằm trong Bài 4: Hình quạt tròn và hình vành khuyên, được VnDoc biên soạn và đăng tải!
