Toán 9 Chân trời sáng tạo Bài 3: Góc ở tâm, góc nội tiếp

Giải Toán 9 trang 90

Khám phá 1 trang 90 Toán 9 Tập 1 CTST

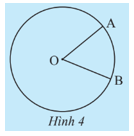
Cho hai điểm A, B trên đường tròn (O; R). Nêu nhận xét về đỉnh và cạnh của \(\widehat {AOB}\).

Hướng dẫn giải

Xét \(\widehat {AOB}\), có:

⦁ Đỉnh là O, trùng với tâm của đường tròn (O; R);

⦁ Hai cạnh là OA, OB là bán kính của đường tròn (O; R).

Thực hành 1 trang 90 Toán 9 Tập 1 CTST

Tính số đo góc ở tâm \(\widehat {EOA}\) và \(\widehat {AOB}\) trong Hình 3. Biết AC và BE là hai đường kính của đường tròn (O).

Hướng dẫn giải

Xét đường tròn (O):

⦁ \(\widehat {EOA}\)=\(\widehat {BOC}\)=57° (đối đỉnh);

⦁\(\widehat {AOB}\)=\(\widehat {COE}\)=\(\widehat {COD}\) + \(\widehat {DOE}\)= 95°+28°=123°.

Giải Toán 9 trang 91

Vận dụng 1 trang 91 Toán 9 Tập 1 CTST

Tính số đo góc ở tâm được tạo thành khi kim giờ quay:

a) Từ 7 giờ đến 9 giờ;

b) Từ 9 giờ đến 12 giờ.

Hướng dẫn giải

Sau 12 giờ, kim giờ sẽ quay được một vòng, ứng với 360°.

Mỗi giờ kim giờ quay được một góc ở tâm có số đo là \(\frac{360°}{12}\)=30°.

a) Từ 7 giờ đến 9 giờ, kim giờ quay một góc ở tâm có số đo là: (9−7)⋅30°=60°.

b) Từ 9 giờ đến 12 giờ, kim giờ quay một góc ở tâm có số đo là: (12−9)⋅30°=90°.

Khám phá 2 trang 91 Toán 9 Tập 1 CTST

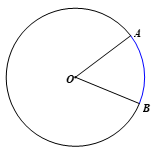
Vẽ vào vở đường tròn (O) và hai điểm A, B nằm trên (O). Dùng bút chì khác màu tô hai phần của đường tròn được phân chia bởi hai điểm A và B.

Hướng dẫn giải

Khám phá 3 trang 91 Toán 9 Tập 1 CTST

Cho OA và OB là hai bán kính vuông góc với nhau của đường tròn (O), C là điểm trên cung nhỏ AB (Hình 7). Ta coi số đo của một cung nhỏ là số đo của góc ở tâm chắn cung đó.

a) Xác định số đo của cung AB.

b) So sánh số đo của hai cung AC⏜ và AB⏜.

Hướng dẫn giải

a) Số đo của cung AB là số đo của \(\widehat {AOB}\) và bằng 90°.

b) Ta có số đo của cung AC là số đo của \(\widehat {AOC}\)

Mà \(\widehat {AOC}\)<\(\widehat {AOB}\) nên số đo của cung AC nhỏ hơn số đo của cung AB.

Giải Toán 9 trang 97

Bài 1 trang 97 Toán 9 Tập 1 CTST

Cho đường tròn (O; 5 cm) và điểm M sao cho OM = 10 cm. Qua M vẽ hai tiếp tuyến với đường tròn tại A và B. Tính số đo góc ở tâm được tạo bởi hai tia OA và OB.

Hướng dẫn giải

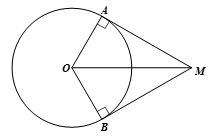
Ta có MA, MB là hai tiếp tuyến tại A và B nên MA \bot OA và MB \bot OB

Xét tam giác MAO vuông tại A, ta có:

\({\rm{cos}}\widehat {MOA} = \frac{{AO}}{{MO}} = \frac{5}{{10}} = \frac{1}{2}\)

Suy ra \(\widehat {MOA}\)= 60^o

Ta có hai tam giác vuông bằng nhau là: \(\Delta MAO = \Delta MBO\) (cạnh huyền- cạnh góc vuông).

Suy ra \(\widehat {MOA} = \widehat {MOB}\)= 60^o

Mà góc ở tâm được tạo bởi hai tia OA và OB là

\(\widehat {AOB} = \widehat {MOA} + \widehat {MOB} = {60^o}.2 = {120^o}\)

Bài2 trang 97 Toán 9 Tập 1 CTST

Cho tam giác đều ABC. Vẽ nửa đường tròn đường kính BC cắt cạnh AB và AC lần lượt tại D và E. Hãy so sánh các cung \(\overset\frown{BD};\overset\frown{BE};\overset\frown{EC}.\)

Hướng dẫn giải

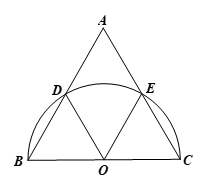
Gọi O là tâm đường tròn đường kính BC.

Ta có OB = OD (= R)

Vậy tam giác BOD cân tại O

Mà \(\widehat {DBO}\)= 60^o nên tam giác BOD đều

Suy ra \(\widehat {DOB}\)= 60^o

OE = DC (= R)

Vậy tam giác EOC cân tại O

Mà\(\widehat {ECO}\)= 60^o nên tam giác EOC đều

Suy ra \(\widehat {EOC}\)= 60^o

Ta có \(\widehat {BOD} + \widehat {DOE} + \widehat {EOC} = {180^o}\)

Suy ra 60^o +\(\widehat {DOE} + {60^o} = {180^o}\) nên \(\widehat {DOE} = {60^o}\)

Vì \(\widehat {BOD} = \widehat {DOE} = \widehat {EOC} = {60^o}\) nên \(sđ\overset\frown{BD} = sđ\overset\frown{BE} = sđ\overset\frown{EC}={{60}^{o}}\)

Vậy \(\overset\frown{BD}=\overset\frown{BE}=\overset\frown{EC}\)

Cho hai đường tròn đồng tâm (O; R) và (O;\(\frac{{R\sqrt 3 }}{2}\)). Một tiếp tuyến của đường tròn nhỏ cắt đường tròn lớn tại hai điểm A và B. Tính số đo cung AB.

Hướng dẫn giải

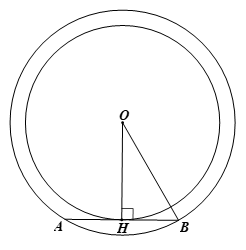
Gọi H là tiếp điểm của tiếp tuyến của đường tròn đã cho.

Xét tam giác OHB vuông tại H, ta có:

\(cos\widehat {HOB}= \frac{{OH}}{{OB}} = \frac{{\frac{{R\sqrt 3 }}{2}}}{R} = \frac{{\sqrt 3 }}{2}\)

suy ra \(\widehat {HOB}\) = 30^o

Ta có OA = OB (= R) nên tam giác OAB cân tại O

Mà OH là đường cao của tam giác AOB

Nên OH cũng là đường phân giác của tam giác AOB

Suy ra \(\widehat {AOB} = 2\widehat {HOB} = {2.30^o} = {60^o}\)

Do đó \(sđ\overset\frown{AB} =\widehat {AOB} = {60^o}.\)

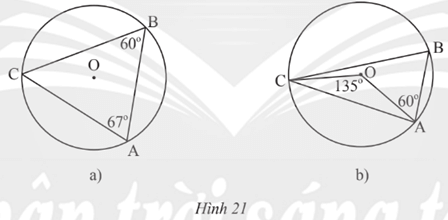
Bài 6 trang 97 Toán 9 Tập 1 CTST

Xác định số đo các cung \(\overset\frown{AB};\overset\frown{BC};\overset\frown{CA}\) trong mỗi hình vẽ sau:

Bài 7 trang 97 Toán 9 Tập 1 CTST

Cho đường tròn (O) có hai đường kính AB, CD vuông góc với nhau. Lấy một điểm M trên cung nhỏ AC rồi vẽ tiếp tuyến với đường tròn (O) tại M. Tiếp tuyến này cắt đường thẳng CD tại S. Chứng minh rằng \(\widehat {MSD} = 2\widehat {MBA}.\)

Hướng dẫn giải

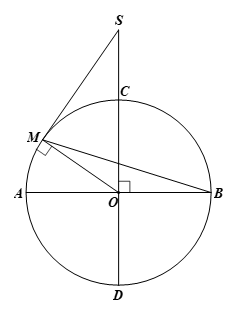
Ta có \(SM \bot OM\) (Tính chất tiếp tuyến)

Suy ra tam giác OSM vuông tại M

Ta có \(\widehat {MSO} + \widehat {MOS} = {90^o}\)

Và \(AB \bot CD\) (gt)

Suy ra \(\widehat {MOS} + \widehat {MOA} = {90^o}\)

Nên \(\widehat {MSO} = \widehat {MOA} hay \widehat {MSD} = \widehat {MOA} (1)\)

Ta có \(\widehat {MOA} = 2\widehat {MBA}\) (góc ở tâm cùng chắn cung AM) (2)

Từ (1) và (2) suy ra \(\widehat {MSD} = 2\widehat {MBA}.\)