Giải Toán 9 trang 85 tập 1 Chân trời sáng tạo
Giải Toán 9 trang 85 Tập 1 Chân trời
Giải Toán 9 trang 85 Tập 1 CTST hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Chân trời sáng tạo tập 1 trang 85.
Thực hành 1 Trang 85 Toán 9 tập 1 Chân trời
Cho đường tròn (J; 5 cm) và đường thẳng c. Gọi K là chân đường vuông góc vẽ từ J xuống c, d là độ dài của đoạn thẳng JK. Xác định vị trí tương đối của đường thẳng c và đường tròn (J; 5 cm) trong mỗi trường hợp sau:
a) d = 4 cm
b) d = 5 cm
c) d = 6 cm
Hướng dẫn giải:
a)
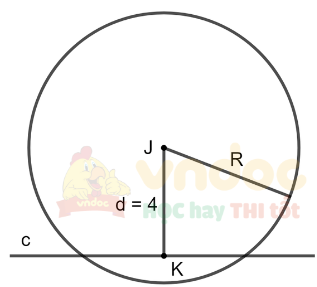
Ta có d < R nên đường thẳng c cắt đường tròn (J; 5 cm)
b)
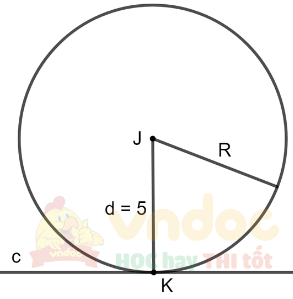
Ta có d = R nên đường thẳng c tiếp xúc với đường tròn (J; 5 cm)
c)
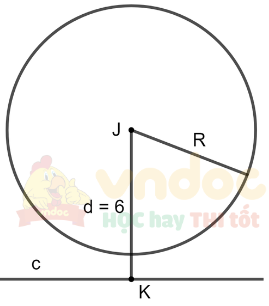
Ta có d > R nên đường thẳng c và đường tròn (J; 5 cm) không giao nhau
Vận dụng 1 Trang 85 Toán 9 tập 1 Chân trời
Một diễn viên xiếc đi xe đạp một bánh trên sợi dây cáp căng được cố định ở hai đầu dây. Biết đường kính bánh xe là 72 cm, tính khoảng cách từ trục bánh xe đến dây cáp.

Hướng dẫn giải:
Ta có sợi dây tiếp xúc với bánh xe nên khoảng cách từ trục bánh xe đến dây cáp bằng R
Vậy khoảng cách từ trục bánh xe đến dây cáp là:
72 : 2 = 36 (cm).
Hoạt động 2 Trang 85 Toán 9 tập 1 Chân trời
Cho điểm A nằm trên đường tròn (O; R), đường thẳng d đi qua A và vuông góc với OA. Gọi M là một điểm trên d (M khác A).
a) Giải thích tại sao ta có OA = R và OM > R.
b) Giải thích tại sao d và (O) không thể có điểm chung nào khác ngoài A.
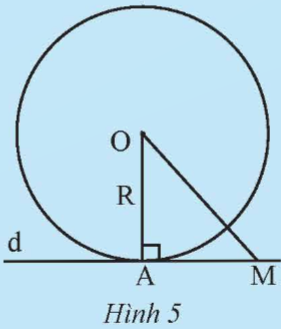
Hướng dẫn giải:
a) Do điểm A nằm trên đường tròn (O; R) nên OA = R
Và OM là đường xiên nên OM > R
b) Giả sử có một điểm chung M khác A
Khi đó OM = R (điều này mâu thuẫn với OM > R)
----------------------------------------------
---> Xem thêm: Giải Toán 9 trang 86 tập 1 Chân trời sáng tạo
Lời giải Toán 9 trang 85 Tập 1 Chân trời sáng tạo với các câu hỏi nằm trong Bài 2: Tiếp tuyến của đường tròn, được VnDoc biên soạn và đăng tải!









