Toán 9 Chân trời sáng tạo Bài 2: Hình nón

Giải Toán 9 Chân trời sáng tạo Bài 2: Hình nón sẽ hướng dẫn giải chi tiết từng bài tập, giúp học sinh ôn tập hiệu quả, chuẩn bị tốt cho các bài kiểm tra và kỳ thi. 

Bài 1 trang 92

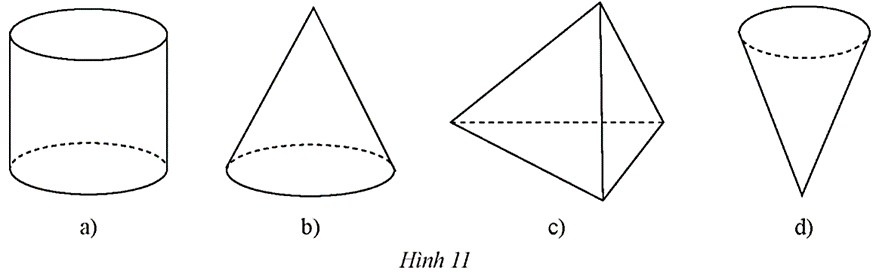
Trong các hình sau đây, hình nào là hình nón?

Lời giải:

Trong Hình 11, ta thấy:

• Hình 11a) là hình trụ;

• Hình 11b) là hình nón;

• Hình 11c) là hình chóp tam giác;

• Hình 11d) là hình nón.

Vậy trong các hình đã cho, hình 11b) và hình 11d) là hình nón.

Bài 2 trang 92 

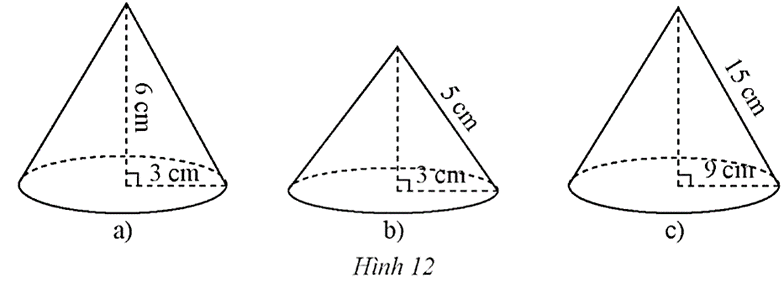
Hãy cho biết chiều cao, bán kính đáy, độ dài đường sinh và diện tích xung quanh của mỗi hình nón sau:

Lời giải:

a) Chiều cao h = 6 cm; bán kính đáy r = 3 cm.

Đường sinh là: \(\sqrt {{6^2} + {3^2}} = 3\sqrt 5\) (cm).

Diện tích xung quanh của hình nón là:

\({S_{xq}} = \pi rl = \pi .3.3\sqrt 5 = 9\pi \sqrt 5\) (cm2).

b) Chiều cao \(h = \sqrt {{l^2} - {r^2}} = \sqrt {{5^2} - {3^2}} = 4\) cm; bán kính đáy r = 3 cm.

Đường sinh là: l = 5cm.

Diện tích xung quanh của hình nón là:

\({S_{xq}} = \pi rl = \pi .3.5 = 15\pi\) (cm2).

c) Chiều cao \(h = \sqrt {{l^2} - {r^2}} = \sqrt {{{15}^2} - {9^2}} = 12\) cm; bán kính đáy r = 9 cm.

Đường sinh là: l = 15cm.

Diện tích xung quanh của hình nón là:

\({S_{xq}} = \pi rl = \pi .9.15 = 135\pi\) (cm2).

Bài 3 trang 92

Tạo lập hình nón có bán kính đáy bằng 4 cm, chiều cao 7 cm.

Lời giải:

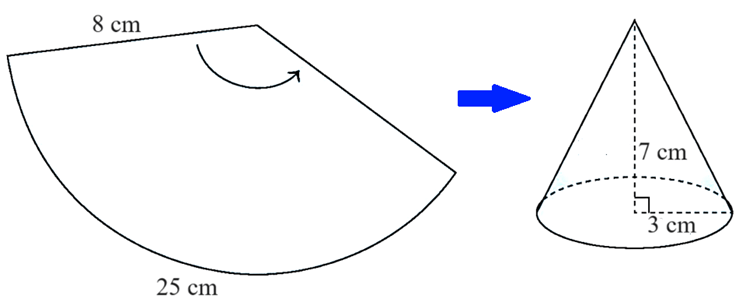
Ta tạo lập hình nón có bán kính đáy bằng 4 cm, chiều cao 7 cm theo các bước sau:

Bước 1: Độ dài đường sinh của hình nón là: \(l=\sqrt{4}2+72=\sqrt{6}5\approx8\)(cm).

Cắt tấm bìa hình quạt tròn có bán kính bằng độ dài đường sinh 8 cm, độ dài cung của hình quạt tròn bằng 8π ≈ 25 (cm).

Bước 2: Cắt tấm bìa hình tròn bán kính 4 cm.

Bước 3: Ghép và dán hai mép quạt lại với nhau sao cho cung của nó tạo thành đường tròn, rồi dán tấm bìa hình tròn ở trên vào làm đáy, ta được hình nón.

Bài 4 trang 92 

Tính thể tích của hình nón biết:

a) Bán kính đáy 6 cm, chiều cao 12 cm;

b) Đường kính của mặt đáy là 7 m, chiều cao 10 m;

c) Diện tích đáy 152 cm², chiều cao 6 cm;

d) Chu vi đáy 130 cm, chiều cao 24 cm.

Lời giải chi tiết

a) Thể tích hình nón là: \(V = \frac{1}{3}Sh = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.6^2}.12 = 144\pi\)(cm3).

b) Bán kính đáy là:\(r = \frac{d}{2} = \frac{7}{2} = 3,5\) (m).

Thể tích hình nón là:\(V = \frac{1}{3}Sh = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi .3,{5^2}.10 =\frac{245}{6}\pi\) (m3).

c) Thể tích hình nón là:

\(V = \frac{1}{3}Sh = \frac{1}{3}152.6 = 304\) (cm3).

d) Bán kính đáy là: \(r = \frac{{130}}{{2\pi }} = \frac{{65}}{\pi }\) (cm).

Thể tích hình nón là:

\(V = \frac{1}{3}Sh = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi .{\left( {\frac{{65}}{\pi }} \right)^2}.24 = \frac{{33800}}{\pi }\)(cm3).

Bài 5 trang 92 

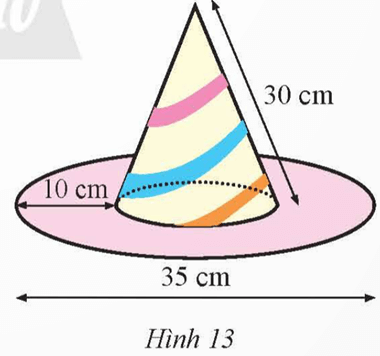
Một cái mũ chú hề có kích thước như Hình 13. Hãy tính tổng diện tích giấy làm nên chiếc mũ (không tính phần hao hụt, kết quả làm tròn đến hàng đơn vị).

Lời giải chi tiết

Diện tích phần làm nón là:

\({S_{xq}} = \pi rl = \pi .\left( {\frac{{35}}{2} - 10} \right).30 = 225\pi\) (cm²).

Diện tích phần làm vành mũ là:

\({S_{vanh}} = \pi {\left( {\frac{{35}}{2}} \right)^2} - \pi .{\left( {\frac{{35}}{2} - 10} \right)^2} = 250\pi\) (cm²).

Tổng diện tích để làm mũ là:

\({S_{xq}} + {S_{vanh}} = 225\pi + 250\pi \approx 1492\)(cm²).