Toán 9 Chân trời sáng tạo Bài 3: Đa giác đều và phép quay
Giải các bài tập trong toán 9 Chân trời sáng tạo Bài 3: Đa giác đều và phép quay trang 75, 77, 78, 79, 80 giúp các em hiểu bài sâu hơn và biết cách vận dụng phép quay để giải quyết các tình huống toán học thực tiễn một cách linh hoạt, sáng tạo.
Mục lục bài viết
Bài 1 trang 79
Gọi tên đa giác đều trong mỗi hình sau và tìm các phép quay có thể biến mỗi hình dưới đây thành chính nó.
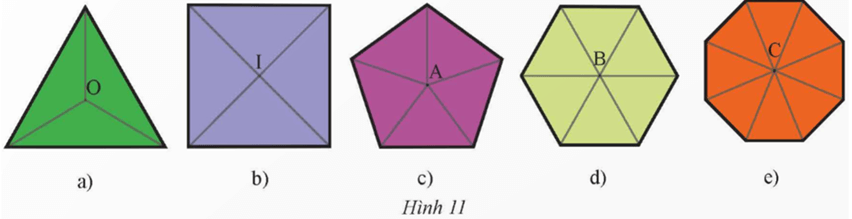
Lời giải:
• Hình 11a) là tam giác đều.
Các phép quay biến tam giác đều thành chính nó là các phép quay 120°, 240° hoặc 360° tâm O cùng chiều hay ngược chiều kim đồng hồ.
• Hình 11b) là hình vuông.
Các phép quay biến hình vuông thành chính nó là các phép quay 90°, 180°, 270°, 360° tâm I cùng chiều hay ngược chiều kim đồng hồ.
• Hình 11c) là ngũ giác đều.
Các phép quay biến ngũ giác đều thành chính nó là các phép quay 72°, 144°, 216°, 288°, 360° tâm A cùng chiều hay ngược chiều kim đồng hồ.
• Hình 11d) là lục giác đều.
Các phép quay biến lục giác đều thành chính nó là các phép quay 60°, 120°, 180°, 240°, 300°, 360° tâm B cùng chiều hay ngược chiều kim đồng hồ.
• Hình11 e) là bát giác đều.
Các phép quay biến bát giác đều thành chính nó là các phép quay 45°, 90°, 135°, 180°, 225°, 270°, 315°, 360° tâm C cùng chiều hay ngược chiều kim đồng hồ.
Bài 2 trang 79
Cho đa giác đều 9 cạnh có tâm O và AB, BC là hai cạnh đa giác (Hình 12).
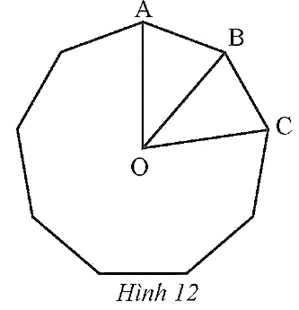
a) Tìm số đo các góc ˆAOB,ˆABO,ˆABC.
b) Tìm các phép quay biến đa giác thành chính nó.
Lời giải chi tiết
a) 9 đỉnh của đa giác chia đường tròn thành 9 phần bằng nhau, số đo mỗi cung là: 360o : 9 = 40o.
Vì 
\(\widehat {AOB}\) là góc nội tiếp chắn cung AB nhỏ
Suy ra \(\widehat {AOB} = {40^o}\).
Do OA = OB (bán kính) nên tam giác AOB cân tại O
Suy ra \(\widehat {OAB} = \widehat {OBA} = \frac{{{{180}^o} - \widehat {AOB}}}{2} = {70^o}\).
Tương tự, ta có \(\widehat {COB} = {40^o}\).
Suy ra \(\widehat {OBC} = \widehat {OCB} = \frac{{{{180}^o} - \widehat {BOC}}}{2} = {70^o}\)
Ta có \(\widehat {ABC} = \widehat {OBA} + \widehat {OBC} = {70^o} + {70^o} = {140^o}\).
b) Các phép quay biến đa giác thành chính nó là các phép quay 40o, 80o, 120o, 160o, 200o, 240o, 280o, 320o hoặc 360o tâm O cùng chiều hay ngược chiều kim đồng hồ.
Bài 3 trang 80
Đường viền ngoài của chiếc đồng hồ trong Hình 13 được làm theo hình đa giác đều nào? Tìm phép quay biến đa giác này thành chính nó.
Lời giải:
Đường viền ngoài của chiếc đồng hồ trong Hình 13 được làm theo hình bát giác đều.
Ta có 8 đỉnh của đa giác được chia thành 8 phần bằng nhau, mỗi cung có số đo 45°.
Do đó, các phép quay biến bát giác đều thành chính nó là 45°, 90°, 135°, 180°, 225°, 270°, 315°, 360° theo chiều hoặc ngược chiều kim đồng hồ.
Bài 4 trang 80
Cho đường tròn (O; R).
a) Vẽ hình tam giác đều, hình vuông, hình lục giác đều có các đỉnh nằm trên (O; R).
b) Tính các cạnh của các hình vừa vẽ theo R.
Lời giải:
a) Hình tam giác đều GHK, hình vuông MNPQ, hình lục giác đều ABCDEF có các đỉnh nằm trên (O; R) được vẽ như hình dưới đây.
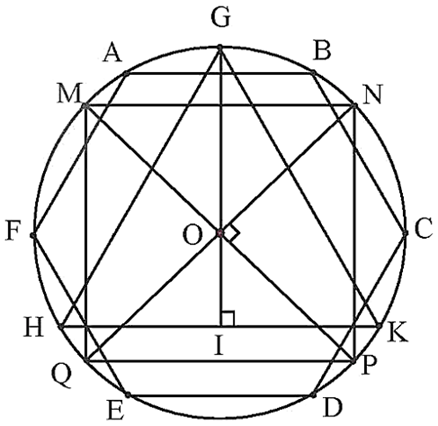
b) • Xét tam giác đều GHK.
Kẻ đường cao GI (I ∈ HK). Xét tam giác GIK vuông tại I, ta có:
GI = \(\frac{3}{2}\)GO = \(\frac{3}{2}\)R;
GI = GK . sin K, suy ra \(GK=GI\sin K=\frac{\frac{3}{2}R}{\frac{\sqrt{3}}{2}}=R\sqrt{3}\).
• Xét hình vuông MNPQ.
Tam giác NOP vuông tại O.
Theo định lí Pythagore, ta có: NP2 = ON2 + OP2 = R2 + R2 = 2R2.
Suy ra NP = \(R\sqrt{2}\).
• Xét hình lục giác đều ABCDEF.
Tam giác AOB có OA = OB và \(\widehat{AOB}\)=360°6=60° nên là tam giác AOB đều.
Suy ra AB = OA = OB = R.
Vậy cạnh của tam giác đều GHK là \(R\sqrt{3}\), cạnh hình vuông MNPQ là \(R\sqrt{2}\) và cạnh hình lục giác đều ABCDEF là R.
Bài 5 trang 80
Tìm các hình phẳng có tính đều:
a) Trong tự nhiên;
b) Trong sản xuất, thiết kế, mĩ thuật.
Lời giải:
a) Các hình phẳng có tính đều trong tự nhiên như con sao biển, bông hoa, lát cam,...
b) Các hình phẳng có tính đều trong sản xuất, thiết kế, mĩ thuật: trang trí nội thất, gạch,...
Bài 6 trang 80
Vòng trong của mái giếng trời hình hoa sen của nhà ga Bến Thành (Thành phố Hồ Chí Minh) có dạng đa giác đều 12 cạnh (Hình 14).
Hãy chỉ ra các phép quay biến đa giác đều thành chính nó.
Lời giải:
Ta có 12 đỉnh của đa giác chia đường tròn thành 12 phần bằng nhau. Số đo mỗi cung là 30°.
Do đó, các phép quay biến đa giác này thành chính nó là các phép quay 30°, 60°, 90°, 120°, 150°, 180°, 210°, 240°, 270°, 300°, 330° hoặc 360° theo chiều kim đồng hồ hay ngược chiều kim đồng hồ.
