VnDoc.com

Toán 9 Chân trời sáng tạo Bài tập cuối chương 9

Bài trước

Tải về

Bài sau

Phân loại: Tài liệu Tính phí

Giải Toán 9 Chân trời sáng tạo Bài tập cuối chương 9 sẽ hướng dẫn giải chi tiết từng bài tập, giúp học sinh ôn tập hiệu quả, chuẩn bị tốt cho các bài kiểm tra và kỳ thi. Thông qua các bài tập tổng hợp, học sinh không chỉ được rèn luyện kỹ năng giải toán mà còn học cách tư duy logic, vận dụng linh hoạt các định lý, công thức và phương pháp đã học.

Bài 1 trang 81

Cho tam giác đều ABC có đường cao AH = 9 cm. Bán kính r của đường tròn nội tiếp tam giác có độ dài là

A. 6 cm.

B. 3 cm.

C. 4,5 cm.

D. $\frac{3\sqrt{3}}{2}cm$ $\frac{3\sqrt{3}}{2}cm$.
Lời giải:

Đáp án đúng là: B

Gọi O là tâm đường tròn nội tiếp tam giác ABC.

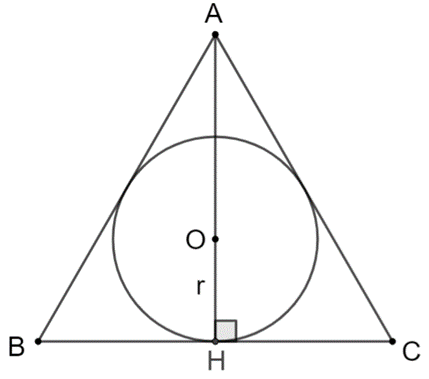
Vì tam giác ABC đều nên cũng AH là đường cao và cũng là đường trung tuyến.

Suy ra O cũng là trọng tâm tam giác ABC.

Khi đó OH = $\frac{1}{3}$ $\frac{1}{3}$AB = $\frac{1}{3}$ $\frac{1}{3}$.9 = 3(cm).

Vậy bán kính r của đường tròn nội tiếp tam giác có độ dài là r = 3 cm.

Bài 2 trang 81

Cho tam giác ABC có AB = AC = 4 cm. Bán kính R của đường tròn ngoại tiếp tam giác có độ dài là

A. $2\sqrt{2}cm$ $2\sqrt{2}cm$.

B. $\sqrt{2}cm$ $\sqrt{2}cm$.

C. $4\sqrt{2}cm$ $4\sqrt{2}cm$.

D. $8\sqrt{2}cm$ $8\sqrt{2}cm$.

Lời giải:

Đáp án đúng là: A

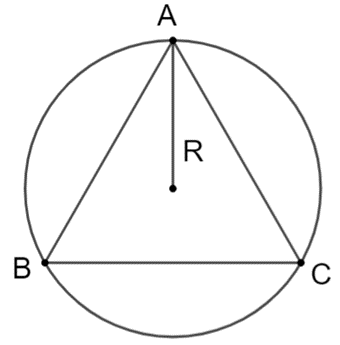
Tâm đường tròn ngoại tiếp của tam giác vuông là trung điểm của BC.

Khi đó $R=\frac{BC}{2}=\frac{\sqrt{A}B^2+AC^2}{2}=2\sqrt{2}$ $R=\frac{BC}{2}=\frac{\sqrt{A}B^2+AC^2}{2}=2\sqrt{2}$(cm).

Vậy bán kính R của đường tròn ngoại tiếp tam giác có độ dài là $2\sqrt{2}$ $2\sqrt{2}$ cm.

Bài 3 trang 81

Tứ giác ở hình nào dưới đây là tứ giác nội tiếp đường tròn (O)?

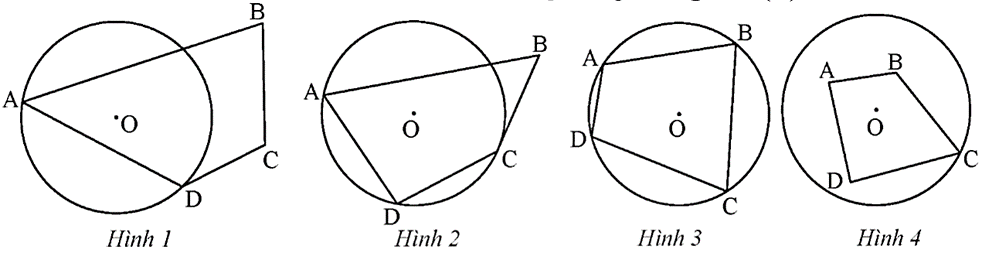
A. Hình 1.

B. Hình 2.

C. Hình 3.

D. Hình 4.

Lời giải:

Đáp án đúng là: C

Trong 4 hình trên chỉ có Hình 3 là tứ giác nội tiếp đường tròn (O) vì cả 4 điểm A, B, C, D đều nằm trên đường tròn.

Bài 4 trang 81

A. Mọi tứ giác luôn nội tiếp đường tròn.

B. Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng 90°.

C. Tổng số đo hai góc đối của một tứ giác nội tiếp luôn bằng 180°.

D. Tất cả các hình thang đều là tứ giác nội tiếp.

Lời giải:

Đáp án đúng là: C

Phát biểu "Tổng số đo hai góc đối của một tứ giác nội tiếp luôn bằng 180°", đây là dấu hiệu nhận biết của tứ giác nội tiếp.

Bài 5 trang 81

Cho tứ giác MNPQ nội tiếp đường tròn (O; R) và $\widehat{M}$ $\widehat{M}$=60°. Số đo góc của $\widehat{P}$ $\widehat{P}$ là

A. 30°.

B. 120°.

C. 180°.

D. 90°.

Lời giải:

Đáp án đúng là: B

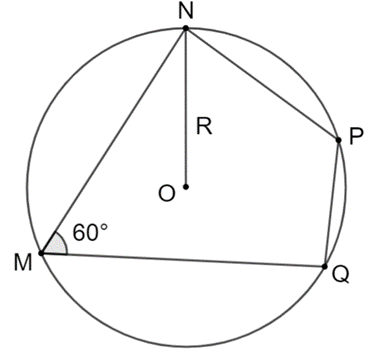
Ta có tứ giác MNPQ nội tiếp có $\widehat{P}$ $\widehat{P}$ và $\widehat{M}$ $\widehat{M}$ là hai góc đối diện nên

$\widehat{P}$ $\widehat{P}$=180°− $\widehat{M}$ $\widehat{M}$=180°−60°=120°.

Vậy $\widehat{P}$ $\widehat{P}$=120°.

Bài 6 trang 81

Cho tứ giác ABCD nội tiếp đường tròn (O). Biết $\widehat {DAO} = 50^{\circ}$ $\widehat {DAO} = 50^{\circ}$, $\widehat {OCD} = 30^{\circ} (Hình 5). Số đo của \widehat {ABC} là$ $\widehat {OCD} = 30^{\circ} (Hình 5). Số đo của \widehat {ABC} là$

A. 80^o.

B. 90^o.

C. 100^o.

D. 110^o.

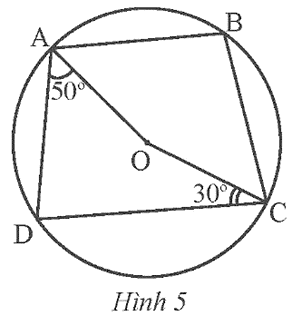
Lời giải chi tiết

OA = OD = R suy ra tam giác AOD cân tại O nên $\widehat {DAO} = \widehat {ADO} = {50^o}$ $\widehat {DAO} = \widehat {ADO} = {50^o}$.

OC = OD = R suy ra tam giác COD cân tại O nên $\widehat {DCO} = \widehat {CDO} = {30^o}$ $\widehat {DCO} = \widehat {CDO} = {30^o}$.

Tứ giác ABCD nội tiếp nên $\widehat {ADC} + \widehat {ABC} = {180^o}$ $\widehat {ADC} + \widehat {ABC} = {180^o}$.

Suy ra $\widehat {ABC} = {180^o} - \widehat {ADC} = {180^o} - \widehat {ADO} - \widehat {CDO} = {180^o} - {30^o} - {50^o} = {100^o}$ $\widehat {ABC} = {180^o} - \widehat {ADC} = {180^o} - \widehat {ADO} - \widehat {CDO} = {180^o} - {30^o} - {50^o} = {100^o}$

Chọn đáp án C.

Bài 7 trang 81

Cho tứ giác ABDC nội tiếp có $\widehat {ACD} = 60^{\circ}$ $\widehat {ACD} = 60^{\circ}$. Khẳng định nào sau đây luôn đúng?

$A. \widehat {ADC} = 60^{\circ} .$ $A. \widehat {ADC} = 60^{\circ} .$

B. $\widehat {ADC} = 120^{\circ}$ $\widehat {ADC} = 120^{\circ}$.

C. $\widehat {ABD} = 60^{\circ}$ $\widehat {ABD} = 60^{\circ}$.

D. $\widehat {ABD} = 120^{\circ}$ $\widehat {ABD} = 120^{\circ}$.

Lời giải chi tiết

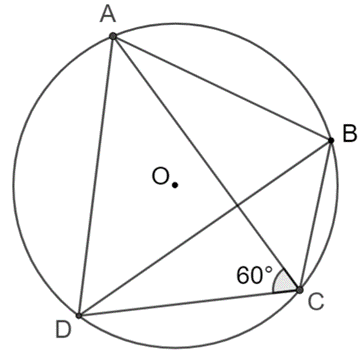
Xét tứ giác ABDC nội tiếp nên $\widehat {ACD} + \widehat {ABD} = 180^\circ$ $\widehat {ACD} + \widehat {ABD} = 180^\circ$

Suy ra $\widehat {ABD} = 180^\circ - \widehat {ACD} = 180^\circ - 60^\circ = 120^\circ$ $\widehat {ABD} = 180^\circ - \widehat {ACD} = 180^\circ - 60^\circ = 120^\circ$

Chọn đáp án D.

Bài 8 trang 82

Cho lục giác đều ABCDEF nội tiếp đường tròn bán kính R. Độ dài cạnh AB bằng

A. R.

B. $R\sqrt{3}$ $R\sqrt{3}$.

C. $\frac{R\sqrt{3}}{2}$ $\frac{R\sqrt{3}}{2}$.

D. $\frac{R}{2}$ $\frac{R}{2}$.

Lời giải:

Đáp án đúng là: A

Ta có lục giác đều được chia thành 6 tam giác đều bằng nhau, mỗi cạnh của tam giác có độ dài bằng R.

Bài 9 trang 82

Cho tam giác đều ABC có O là tâm đường tròn ngoại tiếp. Phép quay nào với O là tâm biến tam giác ABC thành chính nó?

A. 90°.

B. 100°.

C. 110°.

D. 120°.

Lời giải:

Đáp án đúng là: D

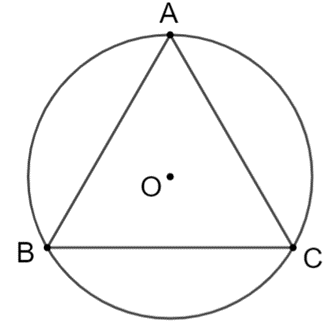
Ta có tam giác đều ABC có 3 đỉnh chia đường tròn tâm (O) thành 3 phần bằng nhau, số đo mỗi cung là: 360° : 3 = 120°.

Vậy phép quay 120° với O là tâm biến tam giác ABC thành chính nó.

Bài 10 trang 82

Cho tam giác nhọn ABC có đường cao AH (H \in BC) và nội tiếp đường tròn tâm O có đường kính AM (hình 6). Chứng minh $\widehat {OAC} = \widehat {BAH}$ $\widehat {OAC} = \widehat {BAH}$.

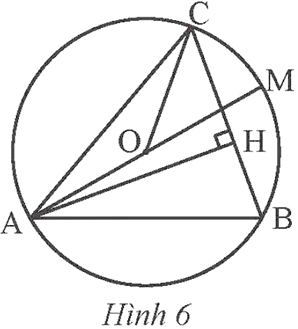
Lời giải chi tiết

OA = OC = R nên $\Delta OAC$ $\Delta OAC$ cân tại O.

Vì $\widehat {ACM}$ $\widehat {ACM}$ là góc nội tiếp chắn cung AM, AM là đường kính đường tròn (O).

Suy ra $\widehat {ACM} = {90^o} hay \widehat {OAC} + \widehat {OCM} = {90^o}$ $\widehat {ACM} = {90^o} hay \widehat {OAC} + \widehat {OCM} = {90^o}$

suy ra $\widehat {OAC} = \widehat {OCA} = {90^o} - \widehat {OCM}$ $\widehat {OAC} = \widehat {OCA} = {90^o} - \widehat {OCM}$

Vì OC = OM = R nên tam giác OMC cân tại O suy ra $\widehat {OCM} = \widehat {OMC}$ $\widehat {OCM} = \widehat {OMC}$.

Do đó $\widehat {OAC} = {90^o} - \widehat {OMC}$ $\widehat {OAC} = {90^o} - \widehat {OMC}$

Vì $\widehat {OMC} và \widehat B$ $\widehat {OMC} và \widehat B$ cùng là góc nội tiếp chắn cung AC nhỏ nên $\widehat {OAC} = {90^o} - \widehat {B} = \widehat {BAH}$ $\widehat {OAC} = {90^o} - \widehat {B} = \widehat {BAH}$ (tổng ba góc trong của tam giác).

Bài 11 trang 82

Cho tam giác ABC vuông tại A (AB < AC) có AH là đường cao. Lần lượt vẽ đường tròn (O) đường kính BH và đường tròn (O’) đường kính HC.

a) Xét vị trí tương đối của hai đường tròn (O) và (O’).

b) Đường tròn (O) cắt AB tại E, đường tròn (O’) cắt AC tại F. Chứng minh rằng tứ giác AEHF là hình chữ nhật.

c) Chứng minh rằng EF là tiếp tuyến đường tròn (O) và đồng thời là tiếp tuyến đường tròn (O’).

d) Đường trung tuyến AM của tam giác ABC cắt EF tại N. Cho biết AB = 6 cm, AC = 8 cm. Tính diện tích tam giác ANF.

Lời giải chi tiết

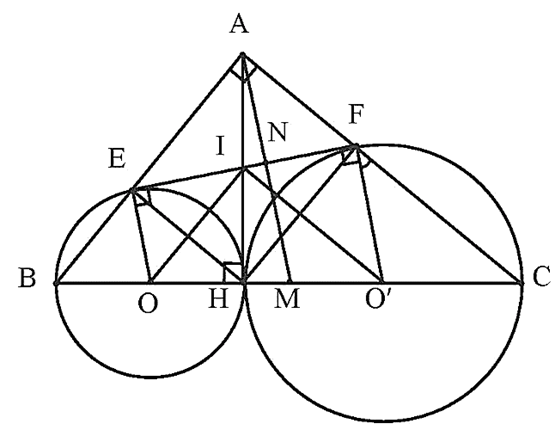
a) Ta có OO’ = OH + O’H = R + R’ suy ra hai đường tròn tiếp xúc nhau.

b) Xét đường tròn (O) có BH là đường kính

$\widehat {BEH}$ $\widehat {BEH}$ là góc nội tiếp chắn nửa đường tròn suy ra $\widehat {BEH}$ $\widehat {BEH}$= 90o hay AB $\bot$ $\bot$ EH tại E.

Xét đường tròn (O’) có HC là đường kính

$\widehat {HFC}$ $\widehat {HFC}$ là góc nội tiếp chắn nửa đường tròn suy ra $\widehat {HFC}$ $\widehat {HFC}$ = 90o hay AC $\bot$ $\bot$ HF tại F.

Xét tứ giác AEHF có:

$\widehat {HEA} = {90^o}$ $\widehat {HEA} = {90^o}$ (chứng minh trên);

$\widehat {EAF} = {90^o}$ $\widehat {EAF} = {90^o}$ (giả thiết);

$\widehat {AFH} = {90^o}$ $\widehat {AFH} = {90^o}$ (chứng minh trên).

Suy ra tứ giác AEHF là hình chữ nhật.

c) Vì OE = OH = R nên $\Delta$ $\Delta$OEH cân tại O suy ra $\widehat {OEH} = \widehat {OHE}$ $\widehat {OEH} = \widehat {OHE}$.

Ta có $\widehat {BHE} = {90^o} - \widehat B$ $\widehat {BHE} = {90^o} - \widehat B$; $\widehat {BAH} = {90^o} - \widehat B$ $\widehat {BAH} = {90^o} - \widehat B$ suy ra $\widehat {BHE} =$ $\widehat {BHE} =$ $\widehat {BAH}$ $\widehat {BAH}$.

Mà $\widehat {OEH} = \widehat {BHE}$ $\widehat {OEH} = \widehat {BHE}$ (chứng minh trên); $\widehat {BAH} = \widehat {AEF}$ $\widehat {BAH} = \widehat {AEF}$ (tính chất hình chữ nhật).

Suy ra $\widehat {OEH} = \widehat {AEF}$ $\widehat {OEH} = \widehat {AEF}$ hay $\widehat {OEH} + \widehat {HEF} = \widehat {AEF} + \widehat {HEF}$ $\widehat {OEH} + \widehat {HEF} = \widehat {AEF} + \widehat {HEF}$ suy ra $\widehat {OEF} = \widehat {AEH} = {90^o}$ $\widehat {OEF} = \widehat {AEH} = {90^o}$.

Nên EF $\bot$ $\bot$ OE tại E; E $\in$ $\in$ (O)

Suy ra EF là đường trung tuyến đường tròn (O) (1).

Vì O’F = O’H = R’ nên tam giác O’HF cân tại O’ suy ra $\widehat {O$ $\widehat {O'HF} = \widehat {O'FH}$

Mà $\widehat {AHF} = \widehat {EFH}$ $\widehat {AHF} = \widehat {EFH}$ (tính chất hình chữ nhật)

Nên $\widehat {O$ $\widehat {O'HF} + \widehat {AFH} = \widehat {O'HF} + \widehat {EFH}$ hay $\widehat {O$ $\widehat {O'FE} + \widehat {AHC} = {90^o}$.

Nên EF $\bot$ $\bot$ O’F tại F; F $\in$ $\in$ (O’)

Suy ra EF là đường trung tuyến đường tròn (O’) (2).

Từ (1) và (2) ta có điều phải chứng minh.

d) Tam giác ABC vuông tại A có AM là đường trung tuyến, suy ra ${{AM}} = {{BM}} = {{CM}} = \frac{1}{2}{{BC}}$ ${{AM}} = {{BM}} = {{CM}} = \frac{1}{2}{{BC}}$.

Do đó $\Delta {{AMC}}$ $\Delta {{AMC}}$ cân tại M , suy ra $\widehat {{{MAC}}} = \widehat {{{MCA}}}$ $\widehat {{{MAC}}} = \widehat {{{MCA}}}$. (1)

Tam giác ${{O}}'{{FC}}$ cân tại ${{O}}'$ (vì ${{O}}'{{F}} = {{O}}'{{C}}$) suy ra $\widehat {{{O}}$ $\widehat {{{O}}'{{FC}}} = \widehat {{{O}}'{{CF}}}$.

Suy ra $\widehat {{{MAC}}} = \widehat {{{O}}$ $\widehat {{{MAC}}} = \widehat {{{O}}'{{FC}}}$.

Mà $\widehat {{{MAC}}},\widehat {O$ $\widehat {{{MAC}}},\widehat {O'FC}$ là hai góc đồng vị nên ${{AM}}//{{O}}'{{F}}$.

Mặt khác ${{O}}'{{F}} \bot {{EF}}$, suy ra ${{AM}} \bot {{EF}}$ ${{AM}} \bot {{EF}}$ tại N .

Xét tam giác ABC vuông tại A có

${{BC}} = \sqrt {{{A}}{{{B}}^2} + {{A}}{{{C}}^2}} = \sqrt {{6^2} + {8^2}} = 10(\;{{cm}})$ ${{BC}} = \sqrt {{{A}}{{{B}}^2} + {{A}}{{{C}}^2}} = \sqrt {{6^2} + {8^2}} = 10(\;{{cm}})$

Diện tích tam giác ABC là

${{{S}}_{\Delta {{ABC}}}} = \frac{1}{2}{{AH}} \cdot {{BC}} = \frac{1}{2}{{AB}} \cdot {{AC}}$ ${{{S}}_{\Delta {{ABC}}}} = \frac{1}{2}{{AH}} \cdot {{BC}} = \frac{1}{2}{{AB}} \cdot {{AC}}$, suy ra ${{AH}} = \frac{{{{AB}} \cdot {{AC}}}}{{{{BC}}}} = \frac{{6 \cdot 8}}{{10}} = 4,8(\;{{cm}})$ ${{AH}} = \frac{{{{AB}} \cdot {{AC}}}}{{{{BC}}}} = \frac{{6 \cdot 8}}{{10}} = 4,8(\;{{cm}})$

Suy ra ${{EF}} = {{AH}} = 4,8\;{{cm}}$ ${{EF}} = {{AH}} = 4,8\;{{cm}}$ (vì AEHF là hình chữ nhật).

Xét tam giác AHF và tam giác ACH có:

$\widehat {AFH} = \widehat {AHC}\left( { = 90^\circ } \right)$ $\widehat {AFH} = \widehat {AHC}\left( { = 90^\circ } \right)$

$\widehat A$ $\widehat A$ chung

Suy ra $\Delta \mathrm{AHF} \backsim \Delta \mathrm{ACH}(\mathrm{g} . \mathrm{g})$ $\Delta \mathrm{AHF} \backsim \Delta \mathrm{ACH}(\mathrm{g} . \mathrm{g})$

nên $\frac{{{{AH}}}}{{{{AC}}}} = \frac{{{{AF}}}}{{{{AH}}}}$ $\frac{{{{AH}}}}{{{{AC}}}} = \frac{{{{AF}}}}{{{{AH}}}}$.

Suy ra ${{AF}} = \frac{{{{A}}{{{H}}^2}}}{{{{AC}}}} = \frac{{4,{8^2}}}{8} = 2,88(\;{{cm}})$ ${{AF}} = \frac{{{{A}}{{{H}}^2}}}{{{{AC}}}} = \frac{{4,{8^2}}}{8} = 2,88(\;{{cm}})$.

Xét tam giác ANF và tam giác CAB có:

$\widehat {ANF} = \widehat {CAB}\left( { = 90^\circ } \right)$ $\widehat {ANF} = \widehat {CAB}\left( { = 90^\circ } \right)$

$\widehat {NAF} = \widehat {ACB}$ $\widehat {NAF} = \widehat {ACB}$ (theo (1)

Suy ra $\Delta \text{ANF}\backsim \Delta CAB(\text{g}.\text{g})$ $\Delta \text{ANF}\backsim \Delta CAB(\text{g}.\text{g})$

Suy ra $\frac{{{S_{\Delta {{ANF}}}}}}{{{S_{\Delta CAB}}}} = {\left( {\frac{{AF}}{{BC}}} \right)^2}$ $\frac{{{S_{\Delta {{ANF}}}}}}{{{S_{\Delta CAB}}}} = {\left( {\frac{{AF}}{{BC}}} \right)^2}$

Diện tích tam giác AFN là:

${{{S}}_{\Delta AFN}} = {\left( {\frac{{AF}}{{BC}}} \right)^2}.{S_{\Delta CAB}} = {\left( {\frac{{2.88}}{{10}}} \right)^2}.\frac{1}{2}.AB.AC = {\left( {\frac{{2.88}}{{10}}} \right)^2}.\frac{1}{2}.6.8 \approx 2\left( {\;{{c}}{{{m}}^2}} \right)$ ${{{S}}_{\Delta AFN}} = {\left( {\frac{{AF}}{{BC}}} \right)^2}.{S_{\Delta CAB}} = {\left( {\frac{{2.88}}{{10}}} \right)^2}.\frac{1}{2}.AB.AC = {\left( {\frac{{2.88}}{{10}}} \right)^2}.\frac{1}{2}.6.8 \approx 2\left( {\;{{c}}{{{m}}^2}} \right)$.

Bài 12 trang 82

Mái nhà trong Hình 7 được đỡ bởi khung đa giác đều. Gọi tên đa giác đó. Tìm phép quay biến đa giác đó thành chính nó.

Lời giải:

Đa giác đều 12 cạnh (gọi là thập nhị giác đều).

Ta có 12 đỉnh của đa giác chia đường tròn thành 12 phần bằng nhau nên số đo mỗi cung là 360° : 12 = 30°.

Gọi O là tâm đường tròn ngoại tiếp của đa giác đều 12 cạnh.

Phép quay 30°, 60°, 90°,…, 360° tâm O cùng hoặc ngược chiều kim đồng hồ biến đa giác đều 12 cạnh thành chính nó.

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

30 lượt tải tài liệu

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Chia sẻ bởi:
Phùng

1

30

Bài trước

Bài sau

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!