Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

Đóng

Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm

Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169

VnDoc.com

Phân loại: Tài liệu Tính phí

Kẹo Ngọt Toán học lớp 9

Hoạt động 1 trang 37 SGK Toán 9 tập 1 Chân trời sáng tạo

Cho trục số được vẽ trên lưới ô vuông đơn vị như Hình 1.

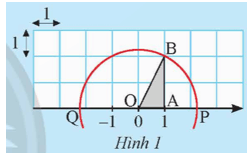
Khám phá 1 trang 37 Toán 9 Tập 1 Chân trời sáng tạo | Giải Toán 9

a) Tính độ dài cạnh huyền OB của tam giác vuông OAB.

b) Vẽ đường tròn tâm O bán kính OB, đường tròn này cắt trục số tại hai điểm P và Q.

Gọi x là số thực được biểu diễn bởi điểm P, y là số thực được biểu diễn bởi điểm Q.

Thay mỗi ? bằng số thích hợp để có các đẳng thức:

x² = ?, y² = ?.

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!

Xóa Đăng nhập để viết

3 Câu trả lời

Bọ Cạp
a) Áp dụng định lí Pythagore vào tam giác vuông OAB ta có:

$OB = \sqrt {1 + {2^2}} = \sqrt 5$

b) Vì P, Q là hai điểm thuộc đường tròn tâm O bán kính OB nên OP = OQ = OB = $\sqrt 5$

Vì x là số thực được biểu diễn bởi điểm P nên x = $\sqrt 5$ ,

y là số thực được biểu diễn bởi điểm Q nên y = - $\sqrt 5$ .

Khi đó ta có các đẳng thức:

${x^2} = {\left( {\sqrt 5 } \right)^2} = 5$

${y^2} = {\left( {-\sqrt 5 } \right)^2} = 5$

0 Trả lời 07/10/24
Bánh Quy
Xem đáp án tại đây: Giải Toán 9 Chân trời sáng tạo Bài 1: Căn bậc hai

0 Trả lời 07/10/24
Bon
Thanks

0 Trả lời 07/10/24