Căn bậc hai
Chuyên đề Toán học lớp 9: Căn bậc hai được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 9 hiệu quả hơn. Mời các bạn tham khảo.
Chuyên đề: Căn bậc hai
A. Lý thuyết
I. CĂN BẬC HAI
1. Khái niệm
Căn bậc hai của một số a không âm là số x sao cho x2 = a
2. Tính chất
- Số âm không có căn bậc hai
- Số 0 có đúng một căn bậc hai đó chính là số 0, ta viết √0 = 0
- Số dương a có đúng hai căn bậc hai là hai số đối nhau; số dương ký hiệu là √a, số âm ký hiệu là -√a
3. Ví dụ cụ thể
- Số 25 có hai căn bậc hai là 5 và -5.
- Số 7 có hai căn bậc hai là √7 và -√7
- Số -1 không có căn bậc hai.
II. CĂN BẬC HAI SỐ HỌC
1. Định nghĩa
- Với số dương a, số √a được gọi là căn bậc hai số học của a.
- Số 0 cũng được gọi là căn bậc hai số học của 0.
- Ta viết x = √a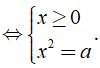 
- Ví dụ:
Căn bậc hai số học của 4 là √4 (= 2).
Căn bậc hai số học của 5 là √5 (≈ = 2,236067977...)
Ví dụ 1: Tìm căn bậc hai số học của các số sau đây:
Giải:
+ Ta có: √121 = 11 vì 11 > 0 và 112 = 121
+ Ta có: √144 = 12 vì 12 > 0 và 122 = 144
+ Ta có: √361 = 19 vì 19 > 0 và 192 = 361
+ Ta có: √400 = 20 vì 20 > 0 và 202 = 400
2. Phép khai phương
- Phép khai phương là phép toán tìm căn bậc hai số học của số không âm (gọi tắt là khai phương).
- Khi biết một căn bậc hai số học của một số, ta dễ dàng xác định được các căn bậc hai của nó.
- Ví dụ:
Căn bậc hai số học của 49 là 7 nên 49 có hai căn bậc hai là 7 và -7.
Căn bậc hai số học cuả 100 là 10 nên 100 có hai căn bậc hai là 10 và -10
Căn bậc hai số học của 144 là 12 nên 144 có hai căn bậc hai là 12 và -12
3. Một số kết quả cần nhớ
- Với a ≥ 0 thì a = (√a)2.
- Với a ≥ 0, nếu x ≥ 0 và x2 = a thì x = √a.
- Với a ≥ 0 và x2 = a thì x = ±√a.
III. SO SÁNH CÁC CĂN BẬC HAI SỐ HỌC
1. Định lý
Với hai số a và b không âm, ta có: a > b ⇔ √a > √b
2. Ví dụ cụ thể: So sánh
- 1 với √2.
Hướng dẫn:
Ta có 1 < 2 ⇒ √1 < √2 ⇒ 1 < √2.
- 3 với √7.
Hướng dẫn:
Ta có 9 > 7 ⇒ √9 > √7 ⇒ 3 > √7.
Ví dụ 1: So sánh:
a) 2 và √3 b) 7 và √51
Giải:
a) Ta có: 2 = √4 mà 4 > 3 nên √4 > √3 tức 2 > √3
b) Ta có: 7 = √49 mà 49 < 51 nên √49 < √51 tức 7 < √49
B. Trắc nghiệm & Tự luận
I. Bài tập trắc nghiệm
Câu 1: Chọn đáp án đúng trong các phương án sau?
A. √2 > √3. B. √5 < 2. C. √7 < 3 D. √-4 = 2.
- Ta có 2 < 3 ⇒ √2 < √3. Đáp án A sai.
- Ta có 5 > 4 ⇒ √5 > √4 ⇒ √5 > 2. Đáp án B sai.
- Ta có 7 < 9 ⇒ √7 < √9 ⇒ √7 < 3. Đáp án C đúng.
- Theo định nghĩa không tồn tại căn bậc hai của số âm. Đáp án D sai.
Chọn đáp án C.
Câu 2: Trong các nhận xét sau, nhận xét nào sai?
A. Căn bậc hai số học của 36 là 6 và -6.
B. 25 có hai căn bậc hai là 5 và -5.
C. Số 0 có đúng một căn bậc hai là chính nó.
D. Số -7 không có căn bậc hai.
- Căn bậc hai số học của 36 là 6. Đáp án A sai.
Chọn đáp án A.
Câu 3: Căn bậc hai số học của -81 là?
A. 9 B. -9 C. ±9 D. Không xác định
Không tồn tại căn bậc hai số học của số âm
Chọn đáp án D.
Câu 4: Một mảnh vườn hình vuông có diện tích bằng diện tích của một hình chữ nhật có chiều dài là 9 m và chiều rộng là 4 m. Hỏi cạnh của mảnh vườn hình vuông đó bằng bao nhiêu?
A. 6m B. 8m C. 7m D. 36m
Diện tích của hình chữ nhật là 9.4 = 36 (m2)
Diện tích của mảnh đất hình vuông là 36 (m2) nên cạnh hình vuông là √36 = 6 (m) (vì độ dài cạnh luôn dương)
Chọn đáp án A.
II. Bài tập tự luận
Câu 1: Tìm căn bậc hai của các số sau: 9; 9/25; 1,21; -144.
- Vì 9 > 0 nên 9 có hai căn bậc hai là 3 và -3, vì 32 = 9 và (-3)2 = 9.
- Vì 9/25 > 0 nên 9/25 có hai căn bậc hai là 3/5 và -3/5, vì (3/5)2 = 9/25 và (-3/5)2 = 9/25.
- Vì 1,21 > 0 nên 1,21 có hai căn bậc hai là 1,1 và -1,1, vì 1,12 = 1,21 và (-1,1)2 = 1,21.
- Theo tính chất, số âm không tồn tại căn bậc hai nên -144 không có căn bậc hai.
Câu 2: Giải các phương trình sau:
a) x2 = 5. b) x2 + 2 = 0 c) (x - 2)2 = 7
Đáp án
- Giải phương trình x2 = 5. Do 5 > 0 nên 5 có hai căn bậc hai là √5 và -√5
Suy ra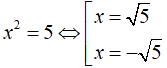 
. Vậy S = {√5; -√5}
- Giải phương trình x2 = -2. Vì -2 < 0 nên -2 không có căn bậc hai. Suy ra phương trình vô nghiệm. Vậy S = ∅
- Giải phương trình (x - 2)2 = 7. Do 7 > 0 nên 7 có hai căn bậc hai là √7 và -√7.
Suy ra
Vậy S = {2 - √7; 2 + √7}
Câu 3: So sánh các số sau:
a) 6 và √35 b) 3 và √5 c) √7 với √5.
a) Ta có: 36 > 35 ⇒ √36 > √35 ⇒ 6 > √35
b) Ta có: 9 > 5 ⇒ √9 > √5 ⇒ 3 > √5
c) Ta có: 7 > 5 ⇒ √7 > √5
Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 9: Căn bậc hai. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 9, Giải bài tập Toán lớp 9 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc
