Giải Toán 9 bài 8: Vị trí tương đối của hai đường tròn (tiếp theo)

Giải SGK Toán 9 bài 8: Vị trí tương đối của hai đường tròn (tiếp theo) hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SKG Toán 9 tập 1, giúp các em nắm vững kiến thức được học, luyện giải Toán 9 hiệu quả. Sau đây mời các bạn tham khảo chi tiết.

A. Trả lời câu hỏi trang 120, 122 SGK Toán 9 tập 1

Trả lời câu hỏi Toán 9 Tập 1 Bài 8 trang 120:

Hãy chứng minh khẳng định trên.

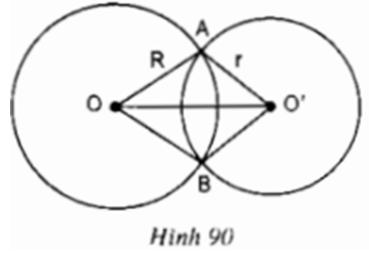
Lời giải

Áp dụng bất đẳng thức tam giác vào tam giác OAO’ ta có:

OA – O’A < OO’ < OA + O’A

⇔ R – r < OO’ < R + r

Trả lời câu hỏi Toán 9 Tập 1 Bài 8 trang 120:

Hãy chứng minh các khẳng định trên.

Lời giải

Hình 91: Hai đường tròn tiếp xúc ngoài tại A nên A nằm giữa OO’

⇒ OA + AO’ = OO’ ⇒ R + r = OO’

Hình 92: Hai đường tròn tiếp xúc trong tại A nên O’ nằm giữa O và A

⇒ OO’ + O’A = OA ⇒ OO’ = OA – O’A = R – r

Trả lời câu hỏi Toán 9 Tập 1 Bài 8 trang 122:

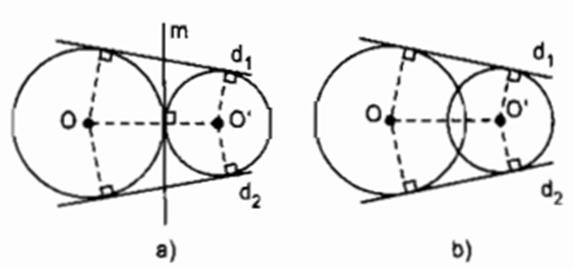
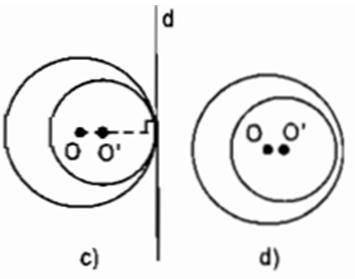
Quan sát các hình 97a, b, c, d trên hình nào có vẽ tiếp tuyến chung của hai đường tròn ? Đọc tên các tiếp tuyến chung đó.

Lời giải

Trả lời: Các tiếp tuyến chung của hai đường tròn là

Hình 97 a) m; d₁; d₂

Hình 97 b) d₁; d₂

Hình 97 c) d

Hình 97 d) Không có tiếp tuyến chung của hai đường tròn

B. Giải bài tập trang 122, 123 SGK Toán 9 tập 1

Bài 35 (trang 122 SGK Toán 9 Tập 1):

Điền vào các ô trống trong bảng, biết rằng hai đường tròn (O; R) và (O'; r) có OO' = d, R < r.

Lời giải:

Ta có bảng sau:

Bài 36 (trang 123 SGK Toán 9 Tập 1):

Cho đường tròn tâm O bán kính OA và đường tròn đường kính OA.

a) Hãy xác định vị trí tương đối của hai đường tròn.

b) Dây AD của đường tròn lớn cắt đường tròn nhỏ ở C. Chứng minh rằng AC = CD.

Lời giải:

Vẽ hình minh họa:

a) Gọi O’ là tâm của đường tròn đường kính OA.

Gọi R và r lần lượt là bán kính đường tròn tâm O và tâm O’. Độ dài OO'=d.

Vì O' là tâm của đường tròn đường kính OA nên \(r=O'A=O'O=\dfrac{OA}2.\)

Vì điểm O' nằm giữa hai điểm O và A nên AO'+OO'=OA

\(\Rightarrow\) OO'=OA-O'A hay d=R-r

Suy ra đường tròn (O) và đường tròn (O') tiếp xúc trong.

b) +) Xét đường tròn (O’) có A, O, C là ba điểm cùng thuộc đường tròn và OA là đường kính nên tam giác AOC vuông tại C.

⇒ OC ⊥ AD

+) Xét đường tròn tâm (O) có A, D là hai điểm thuộc đường tròn nên OA = OD

⇒ ΔAOD cân tại O mà OC ⊥ AD

⇒ OC là đường trung tuyến của ΔAOD

⇒ C là trung điểm của AD

⇒ AC = CD

Bài 37 (trang 123 SGK Toán 9 Tập 1):

Cho hai đường tròn đồng tâm O. Dãy AB của đường tròn lớn cắt đường tròn nhỏ ở C và D. Chứng minh rằng AC = BD.

Lời giải:

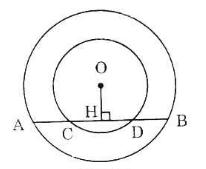
Giả sử vị trí các điểm theo thứ tự là A, C, B, D.

Kẻ OH ⊥ CD. Theo tính chất đường kính vuông góc với một dây ta có:

HA = HB, HC = HD

Nên AC = HA – HC = HB – HD = BD

Vậy AC = BD.

(Trường hợp vị trí các điểm theo thứ tự là A, D, C, B chứng minh tương tự.)

Bài 38 (trang 123 SGK Toán 9 Tập 1):

Điền các từ thích hợp vào chỗ trống (...):

a) Tâm của các đường tròn có bán kính 1cm tiếp xúc ngoài với đường tròn (O; 3cm) nằm trên ...

b) Tâm của các đường tròn có bán kính 1cm tiếp xúc trong với đường tròn (O; 3cm) nằm trên ...

Lời giải:

a) Tâm của các đường tròn có bán kính 1cm tiếp xúc ngoài với đường tròn (O; 3cm) nằm trên đường tròn (O; 4cm).

b) Tâm của các đường tròn có bán kính 1cm tiếp xúc trong với đường tròn (O; 3cm) năm trên đường tròn (O; 2cm).

Bài 39 (trang 123 SGK Toán 9 Tập 1):

Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại A, Kẻ tiếp tuyến chung ngoài BC, B ϵ (O), C ϵ (O'). Tiếp tuyến chung trong tại A cắt tiếp tuyến chung ngoài BC ở I.

a) Chứng minh rằng ∠BAC = 90^o

b) Tính số đo góc OIO'

c) Tính độ dài BC, biết OA = 9cm, O'A = 4cm.

Lời giải:

Vẽ hình minh họa:

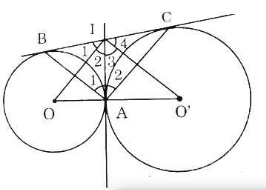
a) Xét đường tròn (O) có IB, IA là hai tiếp tuyến lần lượt tại B,\ A

\(\Rightarrow\) IB=IA

Xét đường tròn (O') có IC, IA là hai tiếp tuyến lần lượt tại C,\ A

\(\Rightarrow\) IC=IA

\(\Rightarrow IB=IC=IA=\dfrac{1}{2}BC\)

Suy ra \(\Delta{ABC}\) vuông tại A (tam giác có đường trung tuyến AI ứng với một cạnh bằng nửa cạnh đó thì tam giác đó là tam giác vuông)

\(\Rightarrow \widehat{BAC}=90^{\circ}.\)

b) Xét đường tròn (O) có IB, IA là hai tiếp tuyến lần lượt tại B, A

\(\Rightarrow\) IO là tia phân giác của góc BIA \(\Rightarrow \widehat{I_1}=\widehat{I_2}\)

Xét đường tròn (O') có IC, IA là hai tiếp tuyến lần lượt tại C,A

\(\Rightarrow\) IO' là tia phân giác của góc CIA \(\Rightarrow \widehat{I_3}=\widehat{I_4}\)

Lại có \(\widehat{I_1}+\widehat{I_2}+\widehat{I_3}+\widehat{I_4}=180^o\)

\(\Leftrightarrow \widehat{I_2}+\widehat{I_2}+\widehat{I_3}+\widehat{I_3}=180^o\)

\(\Leftrightarrow 2\widehat{I_2}+2\widehat{I_3}=180^o\)

\(\Leftrightarrow 2(\widehat{I_2}+\widehat{I_3})=180^o\)

\(\Leftrightarrow \widehat{I_2}+\widehat{I_3}=90^o\)

\(\Leftrightarrow \widehat{OIO'}=90^o\)

c) ΔOIO' vuông tại A có IA là đường cao nên theo hệ thức giữa cạnh và đường cao ta có:

IA² = AO.AO' = 9.4 = 36

=> IA = 6 (cm)

Vậy BC = 2.IA = 2.6 = 12 (cm)

Bài 40 (trang 123 SGK Toán 9 Tập 1):

Đố.

Trên các hình 99a, 99b, 99c, các bánh xe tròn có răng cưa được khớp với nhau. Trên hình nào hệ thống bánh răng chuyển động được? Trên hình nào hệ thống bánh răng không chuyển động được?

Hình 99

Lời giải:

Vì nếu hai đường tròn tiếp xúc ngoài thì hai bánh xe quay theo hai chiều khác nhau (một bánh xe quay cùng chiều quay của kim đồng hồ, bánh xe kia quay ngược chiều của kim đồng hồ). Nếu hai đường tròn tiếp xúc trong thì hai bánh xe quay theo chiều như nhau. Do đó:

- Hình a, b hệ thống bánh răng chuyển động được.

- Hình c, hệ thống bánh răng không chuyển động được.

C. Trắc nghiệm Toán 9 bài 8