Giải Toán 9 bài 5: Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn
Giải bài tập SGK Toán lớp 9 bài 5: Góc có đỉnh ở bên trong đường tròn. Góc có ngoài ở bên trong đường tròn tổng hợp câu hỏi và đáp án cho các câu hỏi trong SGK Toán 9 trang 82, 83, giúp các em nắm vững kiến thức được học trong bài, luyện giải Toán 9 hiệu quả.
Giải bài tập Toán 9 bài 5: Góc có đỉnh ở bên trong đường tròn
Trả lời câu hỏi trang 81, 82 Toán 9 tập 2
Trả lời câu hỏi Toán 9 Tập 2 Bài 5 trang 81:
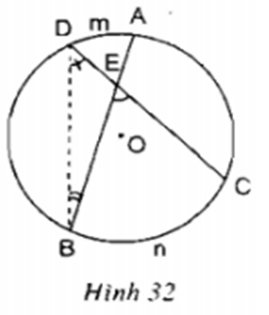
Hãy chứng minh định lý trên.
Hướng dẫn giải
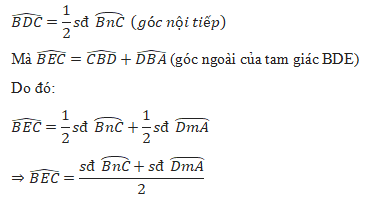
Trả lời câu hỏi Toán 9 Tập 2 Bài 5 trang 82:
Hướng dẫn giải
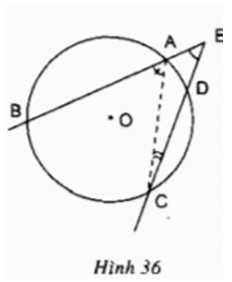
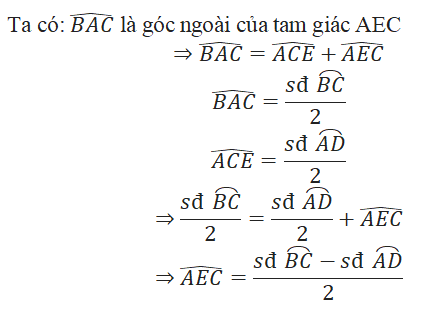
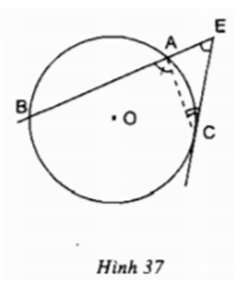
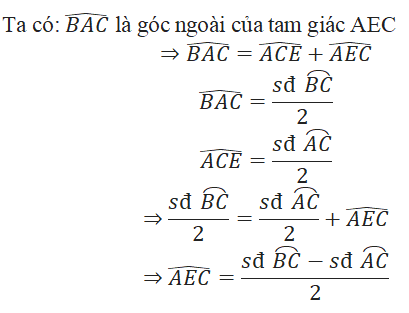
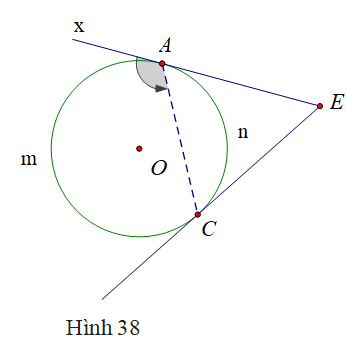
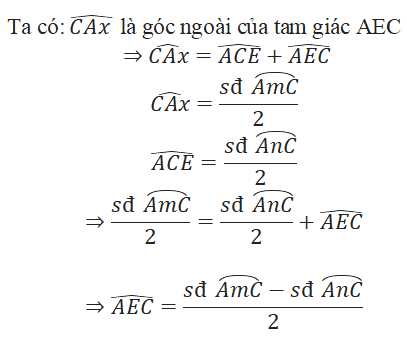
Giải bài tập toán 9 trang 82, 83 Tập 2
Bài 36 (trang 82 SGK Toán 9 Tập 2)
Cho đường tròn (O) và hai dây AB, AC. Gọi M, N lần lượt là điểm chính giữa của cung AB và cung AC. Đường thẳng MN cắt dây AB tại E và cắt dây AC tại H. Chứng minh tam giác AEH là tam giác cân.
Vẽ hình:
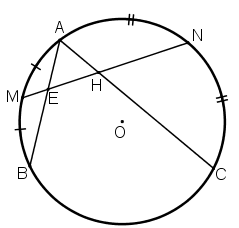
Ta có:  \(\widehat {AHM}= \dfrac{sđ\overparen{AM}+sđ\overparen{NC}}{2}\) (1)
\(\widehat {AHM}= \dfrac{sđ\overparen{AM}+sđ\overparen{NC}}{2}\) (1)
 \(\widehat {AEN}= \dfrac{sđ\overparen{MB}+sđ\overparen{AN}}{2}\), (2)
\(\widehat {AEN}= \dfrac{sđ\overparen{MB}+sđ\overparen{AN}}{2}\), (2)
(Vì ![]() \(\widehat {AHM}\) là góc có đỉnh cố định ở bên trong đường tròn chắn các cung AM và cung NC, và
\(\widehat {AHM}\) là góc có đỉnh cố định ở bên trong đường tròn chắn các cung AM và cung NC, và ![]() \(\widehat {AEN}\) là góc có đỉnh bên trong đường tròn chắn các cung AN và cung MB).
\(\widehat {AEN}\) là góc có đỉnh bên trong đường tròn chắn các cung AN và cung MB).
Theo giả thiết thì:
![]() \(\overparen{AM}=\overparen{MB}\) (3) (M là điểm chính giữa cung AB).
\(\overparen{AM}=\overparen{MB}\) (3) (M là điểm chính giữa cung AB).
![]() \(\overparen{NC}=\overparen{AN}\) (4) N là điểm chính giữa cung AC).
\(\overparen{NC}=\overparen{AN}\) (4) N là điểm chính giữa cung AC).
Từ (1),(2), (3), (4), suy ra ![]() \(\widehat {AHM}= \widehat {AEN}\) do đó ∆AEH là tam giác cân (định nghĩa tam giác cân).
\(\widehat {AHM}= \widehat {AEN}\) do đó ∆AEH là tam giác cân (định nghĩa tam giác cân).
Bài 37 (trang 82 SGK Toán 9 Tập 2)
Cho đường tròn (O) và hai dây AB, AC bằng nhau. Trên cung nhỏ AC lấy một điểm M. Gọi S là giao điểm của AM và BC.
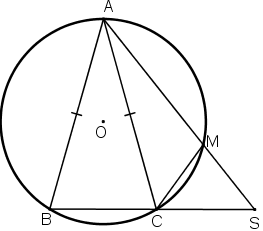
Xét đường tròn (O), ta có:
![]() \(\widehat{ASC}\) là góc có đỉnh ở ngoài đường tròn chắn cung MC và AB.
\(\widehat{ASC}\) là góc có đỉnh ở ngoài đường tròn chắn cung MC và AB.
 \(\Rightarrow \widehat{ASC} = \dfrac{sđ \overparen{AB}- sđ \overparen{MC}}{2}\) (1)
\(\Rightarrow \widehat{ASC} = \dfrac{sđ \overparen{AB}- sđ \overparen{MC}}{2}\) (1)
và  \(\widehat {MCA} = \dfrac{sđ\overparen{AM}}{2}\)(2) (góc nội tiếp chắn cung
\(\widehat {MCA} = \dfrac{sđ\overparen{AM}}{2}\)(2) (góc nội tiếp chắn cung ![]() \(\overparen{AM}\))
\(\overparen{AM}\))
Theo giả thiết thì: AB = AC => ![]() \(\overparen{AB}=\overparen{AC}\) (hai dây bằng nhau căng hai cung bằng nhau).
\(\overparen{AB}=\overparen{AC}\) (hai dây bằng nhau căng hai cung bằng nhau).
![]() \(\Rightarrow sđ\overparen{AB}-sđ\overparen{MC}=sđ\overparen{AC}-sđ\overparen{MC}=sđ\overparen{AM}\) (3)
\(\Rightarrow sđ\overparen{AB}-sđ\overparen{MC}=sđ\overparen{AC}-sđ\overparen{MC}=sđ\overparen{AM}\) (3)
Từ (1), (2), (3) suy ra: ![]() \(\widehat {ASC}=\widehat {MCA}\). (đpcm)
\(\widehat {ASC}=\widehat {MCA}\). (đpcm)
Bài 38 (trang 82 SGK Toán 9 Tập 2)
Trên một đường tròn, lấy liên tiếp ba cung AC, CD, DB sao cho
![]() \(sđ\overparen{AC}=sđ\overparen{CD}=sđ\overparen{DB}=60^0.\) Hai đường thẳng AC và BD cắt nhau tại E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T. Chứng minh rằng:
\(sđ\overparen{AC}=sđ\overparen{CD}=sđ\overparen{DB}=60^0.\) Hai đường thẳng AC và BD cắt nhau tại E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T. Chứng minh rằng:
a) ![]() \(\widehat {AEB}=\widehat {BTC};\)
\(\widehat {AEB}=\widehat {BTC};\)
b) CD là phân giác của ![]() \(\widehat{BCT}.\)
\(\widehat{BCT}.\)
Vẽ hình:
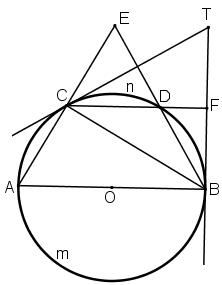
a) Xét đường tròn (O) có ![]() \(sđ\overparen{AC}=sđ\overparen{CD}=sđ\overparen{DB}=60^0\) nên
\(sđ\overparen{AC}=sđ\overparen{CD}=sđ\overparen{DB}=60^0\) nên ![]() \(sđ\overparen{AB}=sđ\overparen{AC}+sđ\overparen{CD}+sđ\overparen{DB}=60^0+60^0+60^0=180^0.\)
\(sđ\overparen{AB}=sđ\overparen{AC}+sđ\overparen{CD}+sđ\overparen{DB}=60^0+60^0+60^0=180^0.\)
Ta có ![]() \(\widehat{AEB}\) là góc có đỉnh ở bên ngoài đường tròn chắn cung CD và AB nên:
\(\widehat{AEB}\) là góc có đỉnh ở bên ngoài đường tròn chắn cung CD và AB nên:
 \(\displaystyle \widehat{AEB}=\dfrac{sđ\overparen{AB}- sđ\overparen{CD}}{2}={{{{180}^0 - {{60}^0}}} \over 2} = {60^0}.\)
\(\displaystyle \widehat{AEB}=\dfrac{sđ\overparen{AB}- sđ\overparen{CD}}{2}={{{{180}^0 - {{60}^0}}} \over 2} = {60^0}.\)
và ![]() \(\widehat{BTC}\) cũng là góc có đỉnh ở bên ngoài đường tròn chắn cung BC lớn và BC nhỏ (hai cạnh đều là tiếp tuyến của đường tròn) nên:
\(\widehat{BTC}\) cũng là góc có đỉnh ở bên ngoài đường tròn chắn cung BC lớn và BC nhỏ (hai cạnh đều là tiếp tuyến của đường tròn) nên:
 \(\widehat{BTC}=\dfrac{sđ\overparen {BAC}-sđ\overparen{BDC}}{2}\displaystyle = {{({{180}^0} + {{60}^0}) - ({{60}^0} + {{60}^0})} \over 2} = {60^0}.\)
\(\widehat{BTC}=\dfrac{sđ\overparen {BAC}-sđ\overparen{BDC}}{2}\displaystyle = {{({{180}^0} + {{60}^0}) - ({{60}^0} + {{60}^0})} \over 2} = {60^0}.\)
Vậy ![]() \(\widehat {AEB} =\widehat {BTC}=60^0.\)
\(\widehat {AEB} =\widehat {BTC}=60^0.\)
b) Xét đường tròn (O) có:
![]() \(\widehat {DCT}\)là góc tạo bởi tiếp tuyến và dây cung chắn cung CD nên:
\(\widehat {DCT}\)là góc tạo bởi tiếp tuyến và dây cung chắn cung CD nên:
 \(\widehat {DCT}=\dfrac{sđ\overparen{CD}}{2}=\dfrac{60^0}{2}=30^0.\)
\(\widehat {DCT}=\dfrac{sđ\overparen{CD}}{2}=\dfrac{60^0}{2}=30^0.\)
![]() \(\widehat {DCB}\) là góc nội tiếp chắn cung BD nên:
\(\widehat {DCB}\) là góc nội tiếp chắn cung BD nên:  \(\displaystyle \widehat {DCB}=\dfrac{sđ\overparen{DB}}{2}={{{{60}^0}} \over 2} = {30^0}.\)
\(\displaystyle \widehat {DCB}=\dfrac{sđ\overparen{DB}}{2}={{{{60}^0}} \over 2} = {30^0}.\)
Vậy ![]() \(\widehat {DCT}=\widehat {DCB}=30^0\)hay CD là phân giác của
\(\widehat {DCT}=\widehat {DCB}=30^0\)hay CD là phân giác của ![]() \(\widehat {BCT}.\)
\(\widehat {BCT}.\)
Giải bài tập toán 9 trang 83 Tập 2: Luyện tập
Bài 39 (trang 83 SGK Toán 9 Tập 2)
Cho AB và CD là hai đường kính vuông góc của đường tròn (O). Trên cung nhỏ BD lây một điểm M . Tiếp tuyến tại M cắt tia AB ở E, đoạn thẳng CM cắt AB ở S.Chứng minh ES = EM.
Vẽ hình minh họa
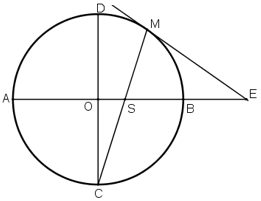
Xét đường tròn (O) có hai đường kính ![]() \(AB \bot CD\) nên
\(AB \bot CD\) nên ![]() \(\widehat{AOC}=\widehat{BOC}=90^0\) nên
\(\widehat{AOC}=\widehat{BOC}=90^0\) nên ![]() \(\overparen{CA}=\overparen{CB}.\)
\(\overparen{CA}=\overparen{CB}.\)
+) Ta có ![]() \(\widehat{MSE}\) là góc có đỉnh nằm trong đường tròn chắn cung AC và cung BM.
\(\widehat{MSE}\) là góc có đỉnh nằm trong đường tròn chắn cung AC và cung BM.
 \(\Rightarrow \widehat{MSE} = \dfrac{sđ\overparen{CA}+sđ\overparen{BM}}{2}\) (1)
\(\Rightarrow \widehat{MSE} = \dfrac{sđ\overparen{CA}+sđ\overparen{BM}}{2}\) (1)
+) ![]() \(\widehat{CME}\) là góc tạo bởi tia tiếp tuyến và dây cung chắn cung CM.
\(\widehat{CME}\) là góc tạo bởi tia tiếp tuyến và dây cung chắn cung CM.
 \(\Rightarrow \widehat{CME}= \dfrac{sđ\overparen{CM}}{2}= \dfrac{sđ\overparen{CB}+sđ\overparen{BM}}{2}\)(2)
\(\Rightarrow \widehat{CME}= \dfrac{sđ\overparen{CM}}{2}= \dfrac{sđ\overparen{CB}+sđ\overparen{BM}}{2}\)(2)
+) Lại có: ![]() \(\overparen{CA}=\overparen{CB}\) (cmt) (3)
\(\overparen{CA}=\overparen{CB}\) (cmt) (3)
Từ (1), (2), (3) ta có:![]() \(\widehat{MSE} = \widehat{CME}\) từ đó ∆ESM là tam giác cân tại E và ES = EM (đpcm).
\(\widehat{MSE} = \widehat{CME}\) từ đó ∆ESM là tam giác cân tại E và ES = EM (đpcm).
Bài 40 (trang 83 SGK Toán 9 Tập 2)
Qua điểm S nằm bên ngoài đường tròn (O), vẽ tiếp tuyến SA và cát tuyến SBC của đường tròn . Tia phân giác của góc BAC cắt dây BC tại D. Chứng minh SA = SD.
Vẽ hình
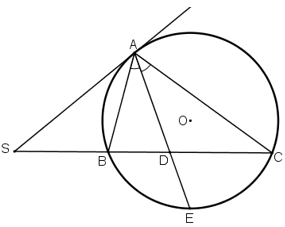
Gọi E là giao điểm thứ hai của AD với đường tròn (O).
Xét đường tròn (O) ta có:
+) ![]() \(\widehat{ADS}\) là góc có đỉnh nằm trong đường tròn chắn cung AB và CE.
\(\widehat{ADS}\) là góc có đỉnh nằm trong đường tròn chắn cung AB và CE.
 \(\Rightarrow \widehat {ADS}=\dfrac{sđ\overparen{AB}+sđ\overparen{CE}}{2}\). (1)
\(\Rightarrow \widehat {ADS}=\dfrac{sđ\overparen{AB}+sđ\overparen{CE}}{2}\). (1)
+) ![]() \(\widehat{SAD}\) là góc tạo bởi tia tiếp tuyến và dây cung chắn cung AE.
\(\widehat{SAD}\) là góc tạo bởi tia tiếp tuyến và dây cung chắn cung AE.
![]() \(\Rightarrow \widehat {SAD}=\dfrac{1}{2} sđ\overparen{AE}\). (2)
\(\Rightarrow \widehat {SAD}=\dfrac{1}{2} sđ\overparen{AE}\). (2)
+) Có: ![]() \(\widehat {BAE} = \widehat {EAC}\) (do AE là phân giác góc BAC
\(\widehat {BAE} = \widehat {EAC}\) (do AE là phân giác góc BAC![]() \(\Rightarrow \overparen{BE}=\overparen{EC}\) (hai góc nội tiếp bằng nhau chắn hai cung bằng nhau).
\(\Rightarrow \overparen{BE}=\overparen{EC}\) (hai góc nội tiếp bằng nhau chắn hai cung bằng nhau).
![]() \(\Rightarrow sđ\overparen{AB} + sđ\overparen{EC} = sđ\overparen{AB} + sđ\overparen{BE}=sđ\overparen{AE}\) (3)
\(\Rightarrow sđ\overparen{AB} + sđ\overparen{EC} = sđ\overparen{AB} + sđ\overparen{BE}=sđ\overparen{AE}\) (3)
Từ (1), (2), (3) ![]() \(\Rightarrow\widehat {ADS}=\widehat {SAD}\Rightarrow\) tam giác SDA cân tại S hay SA=SD.
\(\Rightarrow\widehat {ADS}=\widehat {SAD}\Rightarrow\) tam giác SDA cân tại S hay SA=SD.
Bài 41 (trang 83 SGK Toán 9 Tập 2)
Qua điểm A nằm bên ngoài đường tròn (O) vẽ hai cát tuyến ABC và AMN sao cho hai đường thẳng BN và CM cắt nhau tại một điểm S nằm bên tròn đường tròn.
Chứng minh: ![]() \(\widehat A + \widehat {BSM} = 2\widehat {CMN}.\)
\(\widehat A + \widehat {BSM} = 2\widehat {CMN}.\)
Vẽ hình minh họa:
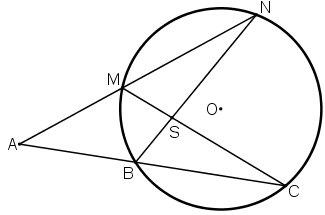
Xét đường tròn (O) có:
+) ![]() \(\widehat A\) là góc có đỉnh nằm ngoài đường tròn (O) chắn cung CN và BM
\(\widehat A\) là góc có đỉnh nằm ngoài đường tròn (O) chắn cung CN và BM  \(\Rightarrow \widehat A = \dfrac{sđ\overparen{CN}-sđ\overparen{BM}}{2} (1)\)
\(\Rightarrow \widehat A = \dfrac{sđ\overparen{CN}-sđ\overparen{BM}}{2} (1)\)
+) ![]() \(\widehat {BSM}\) là góc có đỉnh nằm trong đường tròn (O) chắn cung CN và BM \Rightarrow
\(\widehat {BSM}\) là góc có đỉnh nằm trong đường tròn (O) chắn cung CN và BM \Rightarrow  \(\widehat {BSM}=\dfrac{sđ\overparen{CN}+sđ\overparen{BM}}{2}\) (2)
\(\widehat {BSM}=\dfrac{sđ\overparen{CN}+sđ\overparen{BM}}{2}\) (2)
Cộng (1) và (2) theo vế với vế:
 \(\widehat{A}+\widehat {BSM}=\dfrac{2sđ\overparen{CN}+(sđ\overparen{BM}-sđ\overparen{BM)}}{2}=sđ \overparen{CN}\) (3)
\(\widehat{A}+\widehat {BSM}=\dfrac{2sđ\overparen{CN}+(sđ\overparen{BM}-sđ\overparen{BM)}}{2}=sđ \overparen{CN}\) (3)
Mà ![]() \(\widehat {CMN}\) là góc nội tiếp chắn cung CN
\(\widehat {CMN}\) là góc nội tiếp chắn cung CN  \(\Rightarrow \widehat {CMN}=\dfrac{sđ\overparen{CN}}{2}\)
\(\Rightarrow \widehat {CMN}=\dfrac{sđ\overparen{CN}}{2}\)
![]() \(\Leftrightarrow 2\widehat {CMN}=sđ\overparen{CN}\). (4)
\(\Leftrightarrow 2\widehat {CMN}=sđ\overparen{CN}\). (4)
Từ (3) và (4) ta được: ![]() \(\widehat A + \widehat {BSM} = 2\widehat {CMN}\) (đpcm).
\(\widehat A + \widehat {BSM} = 2\widehat {CMN}\) (đpcm).
Bài 42 (trang 83 SGK Toán 9 Tập 2)
Cho tam giác ABC nội tiếp đường tròn. P,Q,R theo thứ tự là các điểm chính giữa của các cung bị chắn BC, CA, AB bởi các góc A, B, C.
a) Chứng minh AP ⊥ QR.
b) AP cắt CR tại I. Chứng minh tam giác CPI là tam giác cân.
Vẽ hình
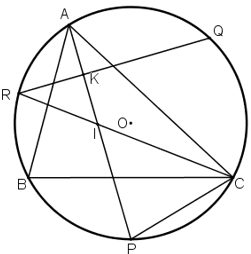
a) Gọi giao điểm của AP và QR là K.
Vì P, Q,R theo thứ tự là các điểm chính giữa các cung bị chắn BC, CA, AB bởi các góc A, B C nên ![]() \(sđ\overparen{AR}=sđ\overparen{RB}=\dfrac {1}{2}sđ\overparen{AB} , sđ\overparen{AQ}=sđ\overparen{QC}=\dfrac {1}{2}sđ\overparen{AC}, sđ\overparen{PC}=sđ\overparen{PB}=\dfrac {1}{2}sđ\overparen{BC}.\)
\(sđ\overparen{AR}=sđ\overparen{RB}=\dfrac {1}{2}sđ\overparen{AB} , sđ\overparen{AQ}=sđ\overparen{QC}=\dfrac {1}{2}sđ\overparen{AC}, sđ\overparen{PC}=sđ\overparen{PB}=\dfrac {1}{2}sđ\overparen{BC}.\)
Suy ra ![]() \(sđ\overparen{AR}+sđ\overparen{QC}+sđ\overparen{CP}=\dfrac {1}{2}sđ\overparen{AB}+\dfrac {1}{2}sđ\overparen{AC}+\dfrac {1}{2}sđ\overparen{BC}\)
\(sđ\overparen{AR}+sđ\overparen{QC}+sđ\overparen{CP}=\dfrac {1}{2}sđ\overparen{AB}+\dfrac {1}{2}sđ\overparen{AC}+\dfrac {1}{2}sđ\overparen{BC}\)
![]() \(\dfrac {1}{2}(sđ\overparen{AB}+sđ\overparen{AC}+sđ\overparen{CB})=\dfrac {1}{2}.360^0=180^0\)
\(\dfrac {1}{2}(sđ\overparen{AB}+sđ\overparen{AC}+sđ\overparen{CB})=\dfrac {1}{2}.360^0=180^0\)
Xét đường tròn (O) ta có:
+) ![]() \(\widehat{AKR}\) là góc có đỉnh ở bên trong đường tròn chắn cung AR và QP nên:
\(\widehat{AKR}\) là góc có đỉnh ở bên trong đường tròn chắn cung AR và QP nên:  \(\widehat{AKR}=\dfrac{sđ\overparen{AR}+sđ\overparen{QP}}{2}=\dfrac{sđ\overparen{AR}+sđ\overparen{QC}+sđ\overparen{CP}}{2}=\dfrac{1}{2}.180^0=90^0.\)
\(\widehat{AKR}=\dfrac{sđ\overparen{AR}+sđ\overparen{QP}}{2}=\dfrac{sđ\overparen{AR}+sđ\overparen{QC}+sđ\overparen{CP}}{2}=\dfrac{1}{2}.180^0=90^0.\)
Vậy ![]() \(\widehat{AKR} = 90^0\) hay
\(\widehat{AKR} = 90^0\) hay ![]() \(AP \bot QR\)
\(AP \bot QR\)
b) Xét đường tròn (O) ta có:
+) ![]() \(\widehat{CIP}\) là góc có đỉnh ở bên trong đường tròn chắn cung AR và CP nên:
\(\widehat{CIP}\) là góc có đỉnh ở bên trong đường tròn chắn cung AR và CP nên:  \(\widehat{CIP}=\dfrac{sđ\overparen{AR}+sđ\overparen{CP}}{2}\) (1)
\(\widehat{CIP}=\dfrac{sđ\overparen{AR}+sđ\overparen{CP}}{2}\) (1)
+) ![]() \(\widehat {PCI}\) góc nội tiếp chắn cung PR, nên
\(\widehat {PCI}\) góc nội tiếp chắn cung PR, nên  \(\widehat {PCI}=\dfrac{sđ\overparen{RB}+sđ\overparen{BP}}{2}\) (2)
\(\widehat {PCI}=\dfrac{sđ\overparen{RB}+sđ\overparen{BP}}{2}\) (2)
Theo giả thiết thì ![]() \(\overparen{AR} = \overparen{RB}\) (3)
\(\overparen{AR} = \overparen{RB}\) (3)
và ![]() \(\overparen{CP} = \overparen{BP}\)(4)
\(\overparen{CP} = \overparen{BP}\)(4)
Từ (1), (2), (3), (4) suy ra: ![]() \(\widehat {CIP}=\widehat {PCI}\). Do đó ∆CPI cân.
\(\widehat {CIP}=\widehat {PCI}\). Do đó ∆CPI cân.
Bài 43 (trang 83 SGK Toán 9 Tập 2)
Cho đường tròn (O) và hai dây cung song song AB, CD (A và C nằm trong cùng một nửa mặt phẳng bờ BD); AD cắt BC tại I. Chứng minh: ![]() \(\widehat{AOC }= \widehat{AIC }.\)
\(\widehat{AOC }= \widehat{AIC }.\)
Vẽ hình
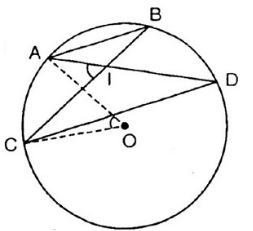
Theo giả thiết:![]() \(\overparen{AC}=\overparen{BD}\) (vì AB // CD) (1)
\(\overparen{AC}=\overparen{BD}\) (vì AB // CD) (1)
Ta có: ![]() \(\widehat{AIC}\) là góc có đỉnh ở trong đường tròn chắn cung AC và cung
\(\widehat{AIC}\) là góc có đỉnh ở trong đường tròn chắn cung AC và cung  \(BD \Rightarrow \widehat{AIC }= \dfrac{sđ\overparen{AC}+sđ\overparen{BD}}{2}\)
\(BD \Rightarrow \widehat{AIC }= \dfrac{sđ\overparen{AC}+sđ\overparen{BD}}{2}\)
Theo (1) suy ra  \(\widehat{AIC }=\dfrac{sđ\overparen{AC}+sđ\overparen{AC}}{2}=\dfrac{2.sđ\overparen{AC}}{2}= sđ\overparen{AC}\) (3)
\(\widehat{AIC }=\dfrac{sđ\overparen{AC}+sđ\overparen{AC}}{2}=\dfrac{2.sđ\overparen{AC}}{2}= sđ\overparen{AC}\) (3)
Mà ![]() \(\widehat{AOC }= sđ\overparen{AC}\) (góc ở tâm chắn cung
\(\widehat{AOC }= sđ\overparen{AC}\) (góc ở tâm chắn cung ![]() \(\overparen{AC}\)) (4)
\(\overparen{AC}\)) (4)
Từ (3), (4), ta có ![]() \(\widehat{AOC } = \widehat{AIC }\) (đpcm).
\(\widehat{AOC } = \widehat{AIC }\) (đpcm).
....................................
Ngoài Giải bài tập SGK Toán lớp 9 bài 5: Góc có đỉnh ở bên trong đường tròn. Góc có ngoài ở bên trong đường tròn, các bạn học sinh còn có thể tham khảo các đề thi học học kì 1 lớp 9, đề thi học học kì 2 lớp 9 mà chúng tôi đã sưu tầm và chọn lọc. Với đề thi học kì 2 lớp 9 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt.








