Giải bài tập SGK Toán lớp 9 bài 1: Phương trình bậc nhất hai ẩn

Toán lớp 9 bài 1: Phương trình bậc nhất hai ẩn

Giải bài tập SGK Toán lớp 9 bài 1: Phương trình bậc nhất hai ẩn. Đây là tài liệu tham khảo hay được VnDoc.com sưu tầm nhằm giúp quá trình ôn tập và củng cố kiến thức chuẩn bị cho kì thi học kì mới môn Toán của các bạn học sinh lớp 9 trở nên thuận lợi hơn. Mời các bạn tham khảo

• Giải bài tập SGK Toán lớp 9 bài 4: Đường thẳng song song và đường thẳng cắt nhau
• Giải bài tập SGK Toán lớp 9 bài 9: Căn bậc ba
• Giải bài toán bằng cách lập hệ phương trình

Bài 1: Phương trình bậc nhất hai ẩn

Bài 1 (trang 7 SGK Toán 9 tập 2): Trong các cặp số (-2; 1), (0; 2), (-1; 0), (1, 5; 3) và (4; -3) cặp số nào là nghiệm của phương trình:

a) 5x + 4y = 8?; b) 3x + 5y = -3?

Lời giải

a) Thay từng cặp số đã cho vào phương trình 5x + 4y = 8, ta được:

5.(-2) + 4.1 = -10 + 4 = -6 ≠ 8 nên cặp số (-2; 1) không là nghiệm của phương trình.

5.0 + 4.2 = 8 nên cặp số (0; 2) là nghiệm của phương trình.

5.(-1) + 4.2 = -5 ≠ 8 nên cặp số (-1; 0) không là nghiệm của phương trình.

5.1,5 + 4.3 = 7,5 + 12 = 19,5 ≠ 8 nên (1,5; 3) không là nghiệm của phương trình.

5.4 + 4.(-3) = 20 – 12 = 8 nên (4; -3) là nghiệm của phương trình.

Vậy có hai cặp số (0; 2) và (4; -3) là nghiệm của phương trình 5x + 4y = 8.

b) Thay từng cặp số đã cho vào phương trình 3x + 5y = -3, ta được:

3.(-2) + 5.1 = -6 + 5 = -1 ≠ -3 nên (-2; 1) không là nghiệm của phương trình.

3.0 + 5.2 = 10 ≠ -3 nên (0; 2) không là nghiệm.

3.(-1) + 5.0 = -3 nên (-1; 0) là nghiệm.

3.1,5 + 5.3 = 4,5 + 15 = 19,5 ≠ -3 nên (1,5; 3) không là nghiệm.

3.4 + 5.(-3) = 12 – 15 = -3 nên (4; -3) là nghiệm.

Vậy có hai cặp số (-1; 0) và (4; -3) là nghiệm của phương trình 3x + 5y = -3.

Bài 2 (trang 7 SGK Toán 9 tập 2): Với mỗi phương trình sau, tìm nghiệm tổng quát của phương trình và vẽ đường thẳng biểu diễn tập nghiệm của nó:

a) 3x - y = 2; b) x + 5y = 3

c) 4x - 3y = -1 d) x + 5y = 0

e) 4x + 0y = -2 f) 0x + 2y = 5

Lời giải

(Lưu ý: Bài làm được trình bày chuẩn theo sgk Toán 9 Tập 2)

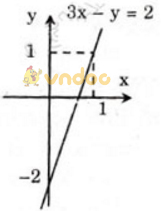
a) 3x - y = 2 ⇔y = 3x - 2

=> Nghiệm tổng quát là (x, 3x - 2) với x \(\in\) R, hoặc

\(\left\{\begin{matrix} x\in R \\ y=3x - 2 \end{matrix}\right.\)

- Vẽ đường thẳng biểu diễn tập nghiệm:

Cho x = 0 => y = -2 được điểm A (0; -2)

Cho x = 1 => y = 1 được điểm B (1; 1)

Biểu diễn cặp số A (0; 2) và B(1;1) trên hệ trục tọa độ và đường thẳng AB chính là tập nghiệm của phương trình 3x - y = 2.

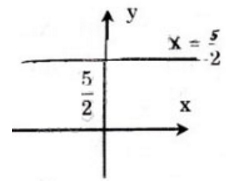
Tập nghiệm là đường thẳng x = - 1/2 , qua A(- 1/2;0) và song song với trục tung.

Bài 3 (trang 7 SGK Toán 9 tập 2): Cho hai phương trình x + 2y = 4 và x – y = 1. Vẽ hai đường thẳng biểu diễn tập nghiệm của hai phương trình đó trên cùng một hệ tọa độ. Xác định tọa độ giao điểm của hai đường thẳng và cho biết tọa độ của nó là nghiệm của các phương trình nào.

Lời giải

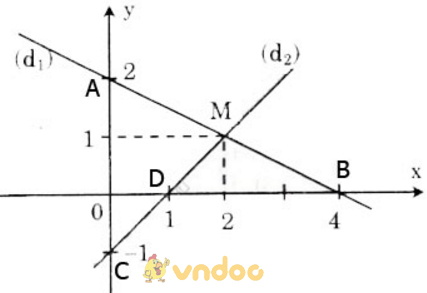
- Vẽ đường thẳng x + 2y = 4.

+ Cho x = 0 => y = 2 được A(0; 2).

+ Cho y = 0 => x = 4 được B(4; 0).

Đường thẳng cần vẽ là đường thẳng (d1) qua A, B.

- Vẽ đường thẳng x – y = 1

+ Cho x = 0 => y = -1 được C(0; -1).

+ Cho y = 0 => x = 1 được D(1; 0).

Đường thẳng cần vẽ là đường thẳng (d2) qua C, D.

- Giao điểm của hai đường thẳng là điểm M có tọa độ là (2; 1).

- Ta có M(2; 1) cùng thuộc hai đường thẳng nên nó là nghiệm của cả hai phương trình đã cho.