Giải Toán 9 bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây

Giải bài tập Toán lớp 9 bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây được VnDoc.com đăng tải tổng hợp đáp án cho các câu hỏi trong SGK Toán 9 trang 106, giúp các em nắm vững kiến thức được học trong bài và luyện giải Toán 9 hiệu quả.

Trả lời câu hỏi Toán 9 Tập 1 Bài 3 trang 105

Hãy sử dụng kết quả của bài toán ở mục 1 để chứng minh rằng:

a) Nếu AB = CD thì OH = OK.

b) Nếu OH = OK thì AB = CD.

Lời giải

OH là một phần đường kính vuông góc với dây AB

⇒ H là trung điểm của AB ⇒ AB = 2HB

OK là một phần đường kính vuông góc với dây CD

⇒ K là trung điểm của CD ⇒ CD = 2KD

Theo mục 1: OH² + HB² = OK² + KD²

a) Ta có: AB = CD ⇒ HB = KD

⇒ OH² = OK² ⇒ OH = OK

b) Ta có: OH = OK ⇒ HB²= KD²

⇒ HB = KD ⇒ AB = CD

Trả lời câu hỏi Toán 9 Tập 1 Bài 3 trang 105

Hãy sử dụng kết quả của bài toán ở mục 1 để so sánh các độ dài:

a) OH và OK, nếu biết AB > CD.

b) AB và CD, nếu biết OH < OK.

Lời giải

a) Nếu AB > CD thì HB > KD

⇒ HB² > KD²

Mà: OH² + HB² = OK² + KD²

⇒ OH² < OK²

⇒ OH < OK

b) Nếu OH < OK thì OH²< OK²

⇒ HB² > KD² ⇒ HB > KD

⇒ AB > CD

Trả lời câu hỏi Toán 9 Tập 1 Bài 3 trang 105

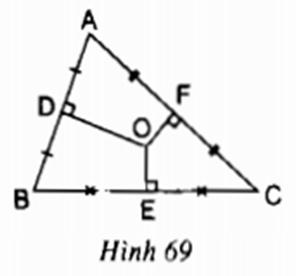
Cho tam giác ABC, O là giao của các đường trung trực của tam giác; D, E, F theo thứ tự là trung điểm của các cạnh AB, BC, AC. Cho biết OD > OE, OE = OF (h.69).

Hãy so sánh các độ dài:

a) BC và AC;

b) AB và AC.

Lời giải

O là giao điểm của 3 đường trung trực của tam giác ABC

⇒ O là tâm đường tròn ngoại tiếp tam giác ABC

a) OE = OF ⇒ AC = BC

b) OD > OE ⇒ AB < AC

Giải Bài 12 trang 106 Toán 9 Tập 1

Cho đường tròn tâm O bán kính 5cm, dây AB bằng 8cm.

a) Tính khoảng cách từ tâm O đến dây AB.

b) Gọi I là điểm thuộc dây AB sao cho AI = 1cm. Kẻ dây CD đi qua I và vuông góc với AB. Chứng minh rằng CD = AB.

Lời giải:

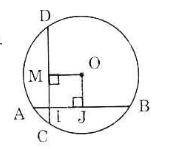
a) Kẻ OJ vuông góc với AB tại J.

Áp dụng định lí Pitago trong tam giác vuông OAJ có:

OJ² = OA² – AJ² = 5² – 4² = 9

=> OJ = 3cm (1)

Vậy khoảng cách từ tâm O đến dây AB là OJ = 3cm.

b) Kẻ OM vuông góc với CD tại M.

Tứ giác OJIM có: ∠J = ∠I = ∠M = 1v nên là hình chữ nhật

Ta có IJ = AJ – AI = 4 – 1 = 3cm

=> OM = IJ = 3cm (Tính chất hình chữ nhật) (2)

Từ (1), (2) suy ra CD = AB (hai dây cách đều tâm thì bằng nhau). (đpcm)

Giải Bài 13 trang 106 Toán 9 Tập 1

Cho đường tròn (O) có các dây AB và CD bằng nhau, các tia AB và CD cắt nhau tại điểm E nằm bên ngoài đường tròn. Gọi H và K theo thứ tự là trung điểm của AB và CD. Chứng minh rằng:

a) EH = EK

b) EA = EC.

Lời giải:

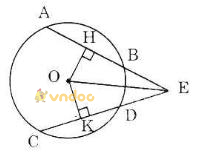
a) Nối OE ta có: AB = CD

=> OH = OK (Định lí 3)

Hai tam giác vuông OEH và OEK có:

OE là cạnh chung

OH = OK

=> ΔOEH = ΔOEK (cạnh huyền, cạnh góc vuông)

=> EH = EK (1). (đpcm)

b) Ta có: OH ⊥ AB

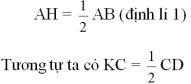
Mà AB = CD (gt) suy ra AH = KC (2)

Từ (1) và (2) suy ra:

EA = EH + HA = EK + KC = EC

Vậy EA = EC. (đpcm)

Giải Bài 14 trang 106 Toán 9 Tập 1

Cho đường tròn tâm O bán kính 25cm, dây AB bằng 40cm. Vẽ dây CD song song với AB và có khoảng cách đến AB bằng 22cm. Tính độ dài dây CD.

Lời giải:

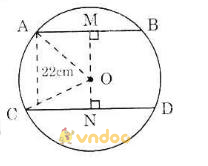
Kẻ OM ⊥ AB, ON ⊥ CD.

Ta thấy M, O, N thẳng hàng. Ta có:

Áp dụng định lí Pitago trong tam giác vuông AMO có:

OM² = OA² – AM² = 25² – 20² = 225

=> OM = √225 = 15cm

=> ON = MN – OM = 22 – 15 = 7 (cm)

Áp dụng định lí Pitago trong tam giác vuông CON có:

CN² = CO² – ON² = 25² – 7² = 576

=> CN = √576 = 24

=> CD = 2CN = 48cm

Giải Bài 15 trang 106 Toán 9 Tập 1

Cho hình 70 trong đó hai đường tròn cùng có tâm là O. Cho biết AB > CD.

Hãy so sánh các độ dài:

a) OH và OK

b) ME và MF

c) MH và MK.

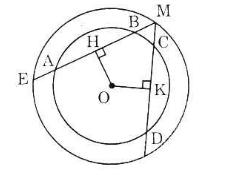
Hình 70

Lời giải:

a) Trong đường tròn nhỏ:

AB > CD => OH < OK (định lí 3)

b) Trong đường tròn lớn:

OH < OK => ME > MF (định lí 3)

c) Trong đường tròn lớn:

ME > MF => MH > MK

Giải Bài 16 trang 106 Toán 9 Tập 1

Cho đường tròn (O), điểm A nằm bên trong đường tròn. Vẽ dây BC vuông góc với OA tại A. Vẽ dây EF bất kì đi qua A và không vuông góc với OA. Hãy so sánh độ dài hai dây BC và EF.

Lời giải:

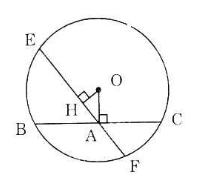
Kẻ OH ⊥ EF.

Trong tam giác vuông OHA vuông tại H có OA > OH (đường vuông góc ngắn hơn đường xiên).

Vì OA > OH nên BC < EF (định lí 3).

Trắc nghiệm Toán 9 bài 3

....................................

Ngoài Giải bài tập Toán lớp 9 bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây, mời các bạn tham khảo thêm tài liệu: Toán lớp 9, Giải bài tập Toán lớp 9, Tài liệu học tập lớp 9 được cập nhật trên VnDoc.

Bài tiếp theo: Giải Toán 9 bài 4: Vị trí tương đối của đường thẳng và đường tròn