Giải Toán 9 Bài 1: Góc ở tâm. Số đo cung

Giải SGK Toán 9 Tập 2 trang 68, 69, 70

Giải Toán 9 Bài 1: Góc ở tâm. Số đo cung hướng dẫn các bạn học sinh trả lời các câu hỏi trong sách giáo khoa Toán lớp 9 trang 69, 70. Thông qua tài liệu này, các bạn học sinh có thể so sánh, đối chiếu với kết quả bài làm của mình, từ đó nâng cao kỹ năng giải Toán 9. Sau đây mời các bạn tham khảo chi tiết.

Bài 1 trang 69 SGK Toán 9 Tập 2

Kim giờ và kim phút của đồng hồ tạo thành một góc ở tâm có số đo là bao nhiêu độ vào những thời điểm sau:

a) 3 giờ;

b) 5 giờ;

c) 6 giờ;

d) 12 giờ;

e) 20 giờ?

Hướng dẫn giải:

Trên mặt đồng hồ người ta chia thành 12 phần bằng nhau. Góc ở tâm tạo bởi hai kim giữa hai số liền nhau là:

360^o : 12 = 30^o

a) Thời điểm 3 giờ (hình a) thì góc ở tâm có số đo là: 3.30^o = 90^o

b) Thời điểm 5 giờ (hình b) thì góc ở tâm có số đo là: 5. 30^o = 150^o

c) Thời điểm 6 giờ (hình c) thì góc ở tâm có số đo là: 6.30^o = 180^o

d) Thời điểm 12 giờ (hình d) thì góc ở tâm có số đo là: 0^o

e) Thời điểm 20 giờ (hình e) thì góc ở tâm có số đo là: 4.30^o= 120^o

Bài 2 trang 69 SGK Toán 9 Tập 2

Cho hai đường thẳng xy và st cắt nhau tại O, trong các góc tạo thành có góc 40^o. Vẽ một đường tròn tâm O. Tính số đo của các góc ở tâm xác định bởi hai trong bốn tia gốc O.

Hướng dẫn giải:

Vẽ hình

Ta có $\widehat {xOs} = 40^\circ$ $\widehat {xOs} = 40^\circ$ , suy ra $\widehat {yOt} = \widehat {xOt} = 40^\circ$ $\widehat {yOt} = \widehat {xOt} = 40^\circ$ (hai góc đối đỉnh)

Lại có $\widehat {xOs} + \widehat {xOt} = 180^\circ$ $\widehat {xOs} + \widehat {xOt} = 180^\circ$(hai góc kề bù) nên $\widehat {xOt} = 180^\circ - \widehat {xOs} = 180^\circ - 40^\circ = 140^\circ .$ $\widehat {xOt} = 180^\circ - \widehat {xOs} = 180^\circ - 40^\circ = 140^\circ .$

Lại có $\widehat {sOy} = \widehat {xOt} = 140^\circ$ $\widehat {sOy} = \widehat {xOt} = 140^\circ$(hai góc đối đỉnh)

Vậy $\widehat {xOt} = \widehat {sOy} = 140^\circ ;\,\widehat {xOs} = \widehat {tOy} = 40^\circ$ $\widehat {xOt} = \widehat {sOy} = 140^\circ ;\,\widehat {xOs} = \widehat {tOy} = 40^\circ$

và $\widehat{xOy} = \widehat{sOt} = 180^{\circ}$ $\widehat{xOy} = \widehat{sOt} = 180^{\circ}$

Bài 3 trang 69 SGK Toán 9 Tập 2

Trên các hình 5, 6 hãy dùng dụng cụ đo góc để tìm số đo cung AmB.

Từ đó, tính số đo cung AnB tương ứng.

Hướng dẫn giải:

Với hình 5: Ta có: $\widehat{AOB} =125^0$ $\widehat{AOB} =125^0$

$=> sđ\overparen{AmB} = 125^0$ $=> sđ\overparen{AmB} = 125^0$

và sđ $\overparen{AnB} = 360^0- 125^0= 235^0$ $\overparen{AnB} = 360^0- 125^0= 235^0$

Với hình 6

Ta có góc $\widehat{AOB} = 65^0$ $\widehat{AOB} = 65^0$

=> sđ $\overparen{AmB} = 65^0$ $\overparen{AmB} = 65^0$

sđ $\overparen{AnB} =360^0-sđ\overparen{ AmB} = 360^0 - 65^0 = 295^0$ $\overparen{AnB} =360^0-sđ\overparen{ AmB} = 360^0 - 65^0 = 295^0$

Bài 4 trang 69 SGK Toán 9 Tập 2

Xem hình 7. Tính số đo của góc ở tâm AOB và số đo cung lớn AB.

Hướng dẫn giải:

Ta có OA = AT (gt) và góc OAT bằng 90^0 nên ∆AOT là tam giác vuông cân tại A, vậy $\widehat{AOB}=45^0.$ $\widehat{AOB}=45^0.$

Suy ra số đo cung nhỏ $\overparen{AB} =\widehat{AOB}= 45^0$ $\overparen{AB} =\widehat{AOB}= 45^0$. Do đó số đo cung lớn $\overparen{AB}$ $\overparen{AB}$ là: $360^0-45^0=315^0$

Bài 5 trang 69 SGK Toán 9 Tập 2

Hai tiếp tuyến của đường tròn (O) tại A và B cắt nhau tại M. Biết góc AMB = 35^o.

a) Tính số đo của góc ở tâm tạo bởi bán kính OA, OB.

b) Tính số đo mỗi cung AB (cung lớn và cung nhỏ).

Hướng dẫn giải:

a) Vì MA,MB là hai tiếp tuyến của $\left( O \right)$ $\left( O \right)$ cắt nhau tại M nên $\widehat {OAM} = 90^\circ ;\,\widehat {MBO} = 90^\circ$ $\widehat {OAM} = 90^\circ ;\,\widehat {MBO} = 90^\circ$

Xét tứ giác OBMA có $\widehat {OAM} + \widehat {OBM} + \widehat {AMB} + \widehat {AOB} = 360^\circ$ $\widehat {OAM} + \widehat {OBM} + \widehat {AMB} + \widehat {AOB} = 360^\circ$(định lý)

Hay $90^\circ + 90^\circ + 35^\circ + \widehat {AOB} = 360^\circ$ $90^\circ + 90^\circ + 35^\circ + \widehat {AOB} = 360^\circ$

$\widehat {AOB} = 145^\circ .$ $\widehat {AOB} = 145^\circ .$

b) Từ $\widehat {AOB} = {145^0}$ $\widehat {AOB} = {145^0}$. Suy ra số đo cung nhỏ $\overparen{AB}$ $\overparen{AB}$ là $145^0$ và số đo cung lớn $\overparen{AB}$ $\overparen{AB}$ là: ${360^0} - {145^0} = {215^0}$ ${360^0} - {145^0} = {215^0}$

Bài 6 trang 69 SGK Toán 9 Tập 2

Cho tam giác đều ABC. Gọi O là tâm của đường tròn đi qua đỉnh A, B, C.

a) Tính số đo các góc ở tâm tạo bởi hai trong ba bán kính OA, OB, OC.

b) Tính số đo các cung tạo bởi hai trong ba điểm A, B, C.

Hướng dẫn giải:

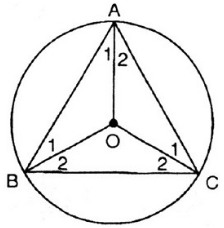a) Ta có: $\widehat A = \widehat B = \widehat C = {60^0}$ $\widehat A = \widehat B = \widehat C = {60^0}$ (gt)

Tâm O của đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của ba cạnh cũng chính là giao điểm của ba đường phân giác của tam giác đều ABC.

Nên $\widehat {{A_1}} = \widehat {{A_2}} = \widehat {{B_1}} = \widehat {{B_2}} = \widehat {{C_1}} = \widehat {{C_2}} = {30^0}$ $\widehat {{A_1}} = \widehat {{A_2}} = \widehat {{B_1}} = \widehat {{B_2}} = \widehat {{C_1}} = \widehat {{C_2}} = {30^0}$

Suy ra: $\widehat {AOB} = {180^0} - \widehat {{A_1}} - \widehat {{B_1}} = {180^0} - {30^0} - {30^0} = {120^0}$ $\widehat {AOB} = {180^0} - \widehat {{A_1}} - \widehat {{B_1}} = {180^0} - {30^0} - {30^0} = {120^0}$

Tương tự ta suy ra: $\widehat {AOB} = \widehat {BOC} = \widehat {COA} = {120^0}$ $\widehat {AOB} = \widehat {BOC} = \widehat {COA} = {120^0}$

b) Từ $\widehat {AOB} = \widehat {BOC} = \widehat {COA} = {120^0}$ $\widehat {AOB} = \widehat {BOC} = \widehat {COA} = {120^0}$ ta suy ra:

sđ $\overparen{AB}=sđ\overparen{CA}=sđ\overparen{CB} = 120^0$ $\overparen{AB}=sđ\overparen{CA}=sđ\overparen{CB} = 120^0$

$sđ\overparen{ABC}=sđ\overparen{BCA}=sđ\overparen{CAB} =360^0- 120^0=240^0$ $sđ\overparen{ABC}=sđ\overparen{BCA}=sđ\overparen{CAB} =360^0- 120^0=240^0$

Bài 7 trang 69 SGK Toán 9 Tập 2

Cho hai đường tròn cùng tâm O với bán kính khác nhau. Hai đường thẳng đi qua O cắt hai đường tròn đó tại các điểm A, B, C, D, M, N, P, Q (h.8).

a) Em có nhận xét gì về số đo của các cung nhỏ AM, CP, BN, DQ?

b) Hãy nêu tên các cung nhỏ bằng nhau.

c) Hãy nêu tên hai cung lớn bằng nhau.

Hướng dẫn giải:

Vẽ hình:

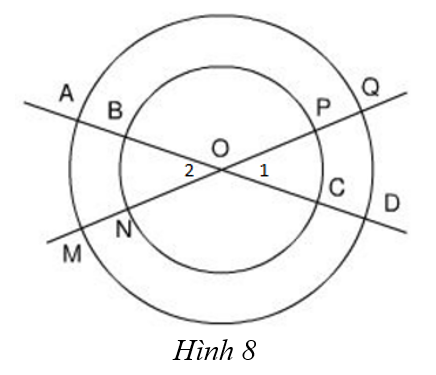
a) Các cung nhỏ $\overparen{AM}, \overparen{CP}, \overparen{BN}, \overparen{DQ}$ $\overparen{AM}, \overparen{CP}, \overparen{BN}, \overparen{DQ}$ có cùng số đo (cùng bằng góc BON)

b) $\overparen{AM} = \overparen{DQ}; \overparen{BN} = \overparen{PC}; \overparen{AQ} =\overparen{ MD}; \overparen{BP} =\overparen{NC}.$ $\overparen{AM} = \overparen{DQ}; \overparen{BN} = \overparen{PC}; \overparen{AQ} =\overparen{ MD}; \overparen{BP} =\overparen{NC}.$

c) Các cung lớn bằng nhau:

$\overparen{AMDQ} = \overparen{MAQD}; \overparen{BNCP} = \overparen{NBPC}$ $\overparen{AMDQ} = \overparen{MAQD}; \overparen{BNCP} = \overparen{NBPC}$

Bài 8 trang 70 SGK Toán 9 Tập 2

Mỗi khẳng định sau đây đúng hay sai? Vì sao?

a) Hai cung bằng nhau thì số đo bằng nhau.

b) Hai cung có số đo bằng nhau thì bằng nhau.

c) Trong hai cung, cung nào có số đo lớn hơn là cung lớn.

d) Trong hai cung trên một đường tròn, cung nào có số đo nhỏ hơn thì nhỏ hơn.

Hướng dẫn giải:

a) Đúng. Dựa vào cách so sánh hai cung (SGK trang 68).

Chú ý: Khi ta nói hai cung bằng nhau, nghĩa là hai cung này so sánh được (tức chúng cùng nằm trong một đường tròn hoặc trong hai đường tròn bằng nhau). Do đó, theo cách so sánh hai cung đã biết thì hai cung bằng nhau thì số đo bằng nhau.

b) Sai. Nếu hai cung này nằm trong hai đường tròn có bán kính khác nhau thì ta không thể so sánh hai cung.

c) Sai. (Lí luận như câu b)

d) Đúng. (Lí luận như câu a)

Bài 9 trang 70 SGK Toán 9 Tập 2

Trên đường tròn tâm O lấy ba điểm A, B, C sao cho $\widehat{AOB} = 100^0$ $\widehat{AOB} = 100^0$, sđ cung $\overparen{AC} = 45^0$ $\overparen{AC} = 45^0$. Tính số đo của cung nhỏ $\overparen{BC}$ $\overparen{BC}$ và cung lớn $\overparen{BC}$ $\overparen{BC}$. (Xét cả hai trường hợp: điểm C nằm trên cung nhỏ $\overparen{AB}$ $\overparen{AB}$, điểm C nằm trên cung lớn $\overparen{AB}$ $\overparen{AB}$

Hướng dẫn giải:

Vẽ hình minh họa

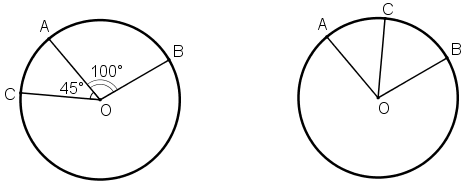
TH1: Điểm C nằm trên cung nhỏ $\overparen{AB}$ $\overparen{AB}$

Số đo cung nhỏ BC là sđ $\overparen{BC}$ $\overparen{BC}$ = sđ $\overparen{AB}-sđ \overparen{AC}= 100^0 – 45^0 = 55^0$ $\overparen{AB}-sđ \overparen{AC}= 100^0 – 45^0 = 55^0$

Số đo cung lớn $\overparen{BC} = 360^0 – 55^0 = 305^0$ $\overparen{BC} = 360^0 – 55^0 = 305^0$

TH2: Điểm C nằm trên cung lớn $\overparen{AB}$ $\overparen{AB}$

Số đo cung nhỏ BC là sđ $\overparen{BC}$ $\overparen{BC}$ = sđ $\overparen{AB}$ $\overparen{AB}$ + sđ $\overparen{AC}= 100^0 + 45^0= 145^0$ $\overparen{AC}= 100^0 + 45^0= 145^0$

Số đo cung lớn $\overparen{BC} = 360^0 – 145^0 = 215^0$ $\overparen{BC} = 360^0 – 145^0 = 215^0$

..................................................

Như vậy VnDoc đã giới thiệu các bạn tài liệu Giải Toán 9 Bài 1: Góc ở tâm. Số đo cung. Hy vọng tài liệu sẽ giúp các em nâng cao kỹ năng giải Toán 9 từ đó học tốt Toán 9 hơn. Để tham khảo lời giải những bài tiếp theo, mời các em vào chuyên mục Giải Toán 9 trên VnDoc nhé. Chuyên mục tổng hợp lời giải theo từng đơn vị bài học giúp các em nắm vững kiến thức được học trong SGK Toán 9. Chúc các em học tốt.

Bài tiếp theo: Giải Toán 9 Bài 2: Liên hệ giữa dây và cung