Giải Toán 9 bài 3: Đồ thị của hàm số y= ax + b (a≠ 0)
Giải Toán 9 bài 3: Đồ thị của hàm số y= ax+ b (a≠ 0) bao gồm đáp án chi tiết cho các câu hỏi trong SGK Toán 9 bài 3. Tài liệu giúp các em dễ dàng trả lời câu hỏi trong bài, luyện giải Toán 9 hiệu quả.
Giải Toán 9 bài 3: Hàm số bậc nhất. Đồ thị của hàm số y= ax+ b (a≠ 0)
A. Trả lời câu hỏi trang 49, 50, 51 SGK Toán 9 tập 1
Câu hỏi 1 trang 49 SGK Toán 9 tập 1
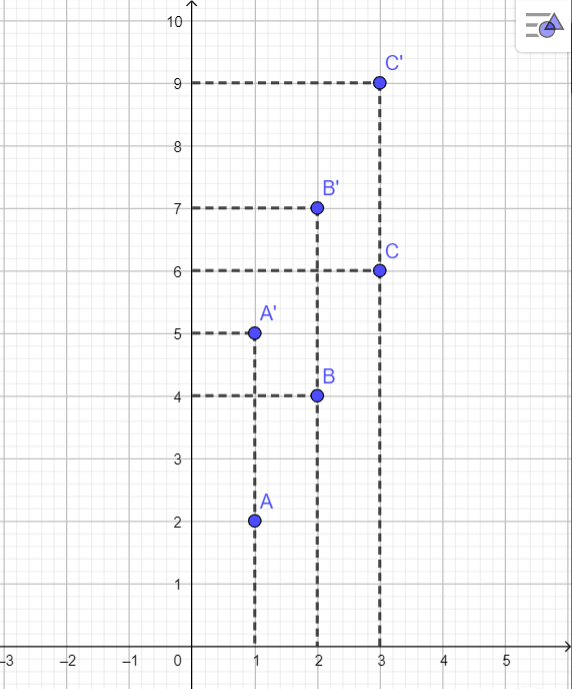
Biểu diễn các điểm sau trên cùng một mặt phẳng tọa độ:
A(1; 2), | B(2; 4) | C(3; 6), |
A’(1; 2 + 3), | B’(2; 4 + 3), | C’(3; 6 + 3). |
Hướng dẫn giải
Câu hỏi 2 trang 49 SGK Toán 9 tập 1
Tính giá trị y tương ứng của các hàm số y = 2x và y = 2x + 3 theo giá trị đã cho của biến x rồi điền vào bảng sau:
Hướng dẫn giải
Câu hỏi 1 trang 51 SGK Toán 9 tập 1
Vẽ đồ thị của các hàm số sau:
| a) y = 2x – 3; | b) y = -2x + 3. |
Hướng dẫn giải
a) y = 2x – 3
Bảng giá trị
x | 0 | 3/2 |
y = 2x – 3 | -3 | 0 |
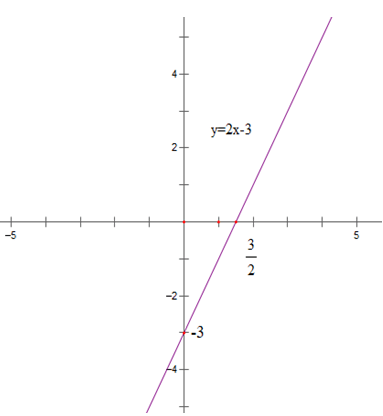
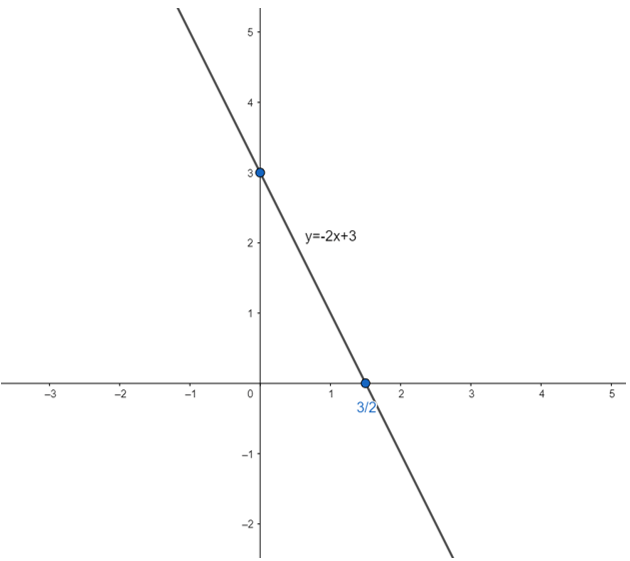
b) y = -2x – 3
Bảng giá trị
x | 0 | 3/2 |
y = -2x – 3 | 3 |
B. Giải bài tập trang 51 SGK Toán 9 tập 1
Bài 15 (trang 51 SGK Toán 9 Tập 1)
a) Vẽ đồ thị của các hàm số 
\(y = 2x;\,\,\,y = 2x + 5;\,\,\,y = - \dfrac{2}{3}x và y = - \dfrac{2}{3}x + 5\) trên cùng một mặt phẳng tọa độ.
b) Bốn đường thẳng trên cắt nhau tạo thành tứ giác OABC (O là gốc tọa độ). Tứ giác OABC có phải là hình bình hành không ? Vì sao ?
Hướng dẫn giải
a) +) Hàm số y = 2x:
Cho x=1\(\Rightarrow y=2.1=2 \Rightarrow M(1; 2)\)
Đồ thị hàm số trên là đường thẳng đi qua gốc O(0;0) và điểm M(1; 2).
+) Hàm số y = 2x + 5:
Cho x=0 \(\Rightarrow y=2.0+5=0+5=5 \Rightarrow B(0; 5).\)
Cho x=-2,5 \(\Rightarrow y=2.(-2,5)+5=-5+5=0\)
⇒ E(-2,5; 0)
Đồ thị hàm số trên là đường thẳng đi qua điểm B(0; 5) và E(-2,5; 0)
+) Hàm số \(y = - \dfrac{2}{3}x:\)
Cho \(x=1 \Rightarrow y=-\dfrac{2}{3}.1=-\dfrac{2}{3} \Rightarrow N {\left(1; -\dfrac{2}{3}\right)}\)
Đồ thị hàm số trên là đường thằng đi qua gốc tọa độ O(0;0) và điểm N \({\left(1; -\dfrac{2}{3}\right)}\)
\(+) Hàm số y = - \dfrac{2}{3}x + 5:\)
Cho x=0 \(\Rightarrow y=-\dfrac{2}{3}.0+5=0+5=5 \Rightarrow B(0; 5)\)
Cho\(x=7,5 \Rightarrow y=-\dfrac{2}{3}.7,5+5=-5 +5=0\)
\(\Rightarrow F(7,5; 0)\)
Đồ thị hàm số là đường thẳng đi qua hai điểm B(0; 5) và F(7,5; 0).
Ta có hình vẽ sau:
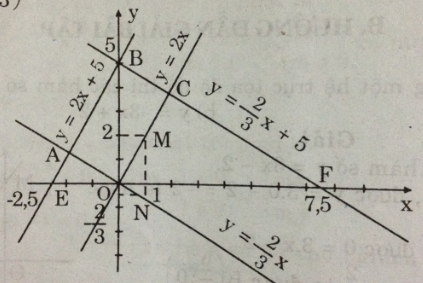
b) Ta có:
+ Đồ thị của hàm số y = 2x song song với đồ thị hàm số y = 2x + 5 \(\Rightarrow\) OC // AB
+ Đồ thị của hàm số \(y=-\dfrac{2}{3}x\) song song với đồ thị hàm số \(y=-\dfrac{2}{3}x+5 \Rightarrow\) OA // BC
Do đó tứ giác OABC là một hình bình hành (dấu hiệu nhận biết).
Bài 16 (trang 51 SGK Toán 9 Tập 1)
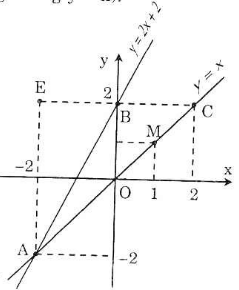
a) Vẽ đồ thị của các hàm số y = x và y = 2x + 2 trên cùng một mặt phẳng tọa độ.
b) Gọi A là giao điểm của hai đồ thị nói trên, tìm tọa độ điểm A.
c) Vẽ qua điểm B(0; 2) một đường thẳng song song với trục Ox, cắt đường thẳng y = x tại điểm C. Tìm tọa độ điểm C rồi tính diện tích tam giác ABC (đơn vị đo trên các trục tọa độ là xentimet)
Hướng dẫn giải
a) Vẽ đường thẳng qua O(0; 0) và điểm M(1; 1) được đồ thị hàm số y = x.
Vẽ đường thẳng qua B(0; 2) và A(-2; -2) được đồ thị hàm số y = 2x + 2.
b) Hoành độ giao điểm của 2 đồ thị hàm số là nghiệm của phương trình:
2x + 2 = x
=> x = -2 => y = -2
Suy ra tọa độ giao điểm là A(-2; -2).
c) Qua B(0; 2) vẽ đường thẳng song song với Ox, đường thẳng này có phương trình y = 2 và cắt đường thẳng y = x tại C.
- Tọa độ điểm C:
Hoành độ giao điểm của 2 đồ thị hàm số là nghiệm của phương trình:
x = 2 => y = 2 => tọa độ C(2; 2)
- Tính diện tích tam giác ABC: (với BC là đáy, AE là chiều cao tương ứng với đáy BC)
Kẻ \(AE \bot BC\), ta có AE=2+2=4 và BC=2
Tam giác \(\Delta{ABC}\) có AE là đường cao ứng với cạnh BC.
Diện tích \(\Delta{ABC}\) là:
\(S=\dfrac{1}{2}.AE.BC=\dfrac{1}{2}.4.2=4 (cm^2).\)
C. Giải bài tập Toán 9 trang 51, 52 tập 1: Luyện tập
Bài 17 (trang 51 SGK Toán 9 Tập 1)
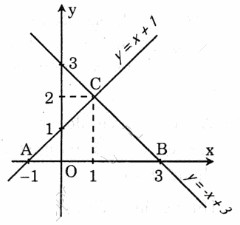
a) Vẽ đồ thị của các hàm số y = x+1 và y = −x + 3 trên cùng một mặt phẳng tọa độ.
b) Hai đường thẳng y = x+1 và y=−x+3 cắt nhau tại C và cắt trục Ox theo thứ tự tại A và B. Tìm tọa độ của các điểm A, B, C.
c) Tính chu vi và diện tích của tam giác ABC (đơn vi đo trên các trục tọa độ là xentimét)
Giải:
a) Xem hình dưới đây:
b) Qua đồ thị, dễ dàng tìm được tọa độ của các điểm A, B, C bằng:
A(−1;0), B(3;0), C(1;2)
c) Chu vi của tam giác ABC là:
\(AB+BC+AC=4+2\sqrt{2}+2\sqrt{2}=4+4\sqrt{2}\left(cm\right)\)
Diện tích tích của tam giác ABC là:
\(S=\frac{1}{2}AB.2=4\left(cm^2\right)\)
Bài 18 (trang 52 SGK Toán 9 Tập 1)
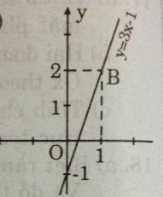
a) Biết rằng với x = 4 thì hàm số y = 3x + b có giá trị là 11. Tìm b. Vẽ đồ thị của hàm số với giá trị b vừa tìm được.
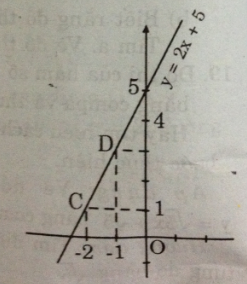
b) Biết rằng đồ thị của hàm số y = ax + 5 đi qua điểm A (-1; 3). Tìm a. Vẽ đồ thị của hàm số với giá trị a vừa tìm được.
Giải:
a) Thay x = 4 và y = 11 vào y = 3x + b ta được:
11 = 3.4 + b = 12 + b
=> b = 11 – 12 = -1
Ta được hàm số y = 3x – 1
- Cho x = 0 => y = -1 được A(0; -1)
- Cho x = 1 => y = 2 được B(1; 2).
Nối A, B ta được đồ thị hàm số y = 3x – 1.
b) Thay tọa độ điểm A(-1; 3) vào phương trình y = ax + 5 ta có:
3 = a(-1) + 5
=> a = 5 – 3 = 2
Ta được hàm số y = 2x + 5.
- Cho x = -2 => y = 1 được C(-2; 1)
- Cho x = -1 => y = 3 được D(-1; 3)
Nối C, D ta được đồ thị hàm số y = 2x + 5.
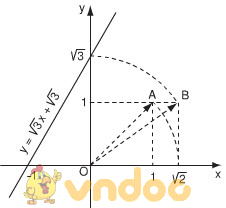
Bài 19 (trang 52 SGK Toán 9 Tập 1)
Đồ thị của hàm số \(y=\sqrt{3x}+\sqrt{3}\) được vẽ bằng compa và thước thẳng.
Hãy tìm hiểu cách vẽ đó rồi nêu lại các bước thực hiện.
Áp dụng: Vẽ đồ thị của hàm số \(y=\sqrt{5x}+\sqrt{5}\) bằng compa và thước thẳng.
Hướng dẫn. Tìm điểm trên trục tung có tung độ bằng \(\sqrt{5}\).
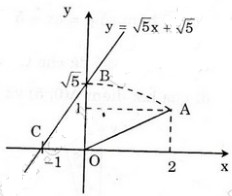
Giải:
Hình trên diễn tả cách dựng đoạn thẳng có độ dài bằng \(\sqrt{5}\)
Đồ thị hàm số \(y=\sqrt{5x}+\sqrt{5}\) đi qua hai điểm \(A\left(0;\sqrt{5}\right)\) và \(B\left(-1;0\right)\)
D. Trắc nghiệm Đồ thị hàm số Y = ax + b
..................................................
Ngoài Giải Giải Toán 9 bài 3: Đồ thị của hàm số y= ax+ b (a≠ 0), mời các bạn tham khảo thêm tài liệu: Toán lớp 9, Giải bài tập Toán lớp 9, Tài liệu học tập lớp 9.
Bài tiếp theo
