Giải Toán 9 bài 4: Giải hệ phương trình bằng phương pháp cộng đại số

Giải bài tập SGK Toán lớp 9 bài 4: Giải hệ phương trình bằng phương pháp cộng đại số là tài liệu tham khảo hữu ích dành cho các bạn học sinh, giúp các bạn ôn luyện kiến thức đồng thời cũng giúp học sinh học tốt môn Toán lớp 9. Mời các bạn tham khảo chi tiết bài viết dưới đây nhé.

Lý thuyết Giải hệ phương trình bằng phương pháp cộng đại số

1. Quy tắc cộng đại số

Quy tắc cộng đại số dùng để biến đổi một hệ phương trình thành hệ phương trình tương đương. Quy tắc cộng đại số gồm hai bước:

Bước 1: Cộng hay trừ từng vế hai phương trình của hệ phương trình đã cho để được một phương trình mới.

Bước 2: Dùng phương trình mới ấy thay thế cho một trong hai phương trình của hệ (và giữ nguyên phương trình kia) ta được hệ phương trình mới tương đương với hệ đã cho.

2. Cách giải hệ phương trình bằng phương pháp cộng đại số

Bước 1: Nhân các vế của hai phương trình với số thích hợp (nếu cần) sao cho các hệ số của một ẩn nào đó trong hai phương trình của hệ bằng nhau hoặc đối nhau.

Bước 2: Sử dụng quy tắc cộng đại số để được hệ phương trình mới, trong đó có một phương trình mà hệ số của một trong hai ẩn bằng 0 (tức là phương trình một ẩn).

Bước 3: Giải phương trình một ẩn vừa thu được rồi suy ra nghiệm của hệ đã cho.

3. Chú ý

+ Trong phương pháp cộng đại số, trước khi thực hiện bước 1, có thể nhân hai vế của mỗi phương trình với một số thích hợp (nếu cần) sao cho các hệ số của một ẩn nào đó trong hai phương trình của hệ là bằng nhau hoặc đối nhau.

+ Đôi khi ta có thể dùng phương pháp đặt ẩn phụ để đưa hệ phương trình đã cho về hệ phương trình với hai ẩn mới, rồi sau đó sử dụng một trong hai phương pháp giải ở trên.

4. Các dạng toán thường gặp

• Dạng 1: Giải hệ phương trình bằng phương pháp cộng đại số
• Dạng 2: Giải hệ phương trình đưa về hệ phương trình bậc nhất hai ẩn
• Dạng 3: Giải hệ phương trình bằng phương pháp đặt ẩn phụ
• Dạng 4: Tìm điều kiện của tham số để hệ phương trình thỏa mãn điều kiện cho trước

Trả lời câu hỏi Toán 9 Tập 2 Bài 4 trang 17

Áp dụng quy tắc cộng đại số để biến đồi hệ (I), nhưng ở bước 1, hãy trừ từng vế hai phương trình của hệ (I) và viết ra các hệ phương trình mới thu được.

Lời giải

Trừ từng vế hai phương trình của hệ (I) ta được phương trình:

(2x – y) – (x + y) = 1 – 2 hay x – 2y = -1

Khi đó, ta thu được hệ phương trình mới:

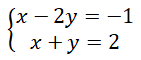
Trả lời câu hỏi Toán 9 Tập 2 Bài 4 trang 17

Các hệ số của y trong hai phương trình của hệ (II) có đặc điểm gì?

Lời giải

Hệ số của y trong hai phương trình của hệ (II) đối nhau (có tổng bằng 0)

Trả lời câu hỏi Toán 9 Tập 2 Bài 4 trang 18

a) Nếu nhận xét về các hệ số của x trong hai phương trình của hệ (III).

b) Áp dụng quy tắc cộng đại số, hãy giải hệ (III) bằng cách trừ từng vế hai phương trình của (III).

Lời giải

a) Hệ số của x trong hai phương trình của hệ (III) giống nhau

Lấy phương trình thứ nhất trừ đi phương trình thứ hai vế với vế, ta được: 5y = 5

Do đó

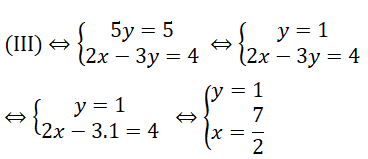
Vậy hệ phương trình có nghiệm duy nhất (7/2;1)

Trả lời câu hỏi Toán 9 Tập 2 Bài 4 trang 18

Giải tiếp hệ (IV) bằng phương pháp đã nêu ở trường hợp thứ nhất.

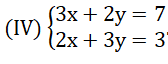
Lời giải

Lấy phương trình thứ nhất trừ đi phương trình thứ hai vế với vế, ta được: -5y = 5

Do đó

Vậy hệ phương trình có nghiệm duy nhất (3; -1)

Trả lời câu hỏi Toán 9 Tập 2 Bài 4 trang 18

Nêu một cách khác để đưa hệ phương trình (IV) về trường hợp thứ nhất?

Lời giải

Chia cả 2 vế của phương trình thứ nhất cho 3 và 2 vế của phương trình thứ hai cho 2 ta được:

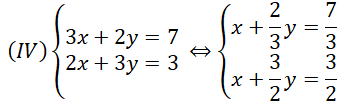
Bài 20 trang 18 SGK Toán 9 tập 2

Giải các hệ phương trình sau bằng phương pháp cộng đại số.

e)

Hướng dẫn giải:

a. \(\left\{ \begin{matrix} 3x+y=3 \\ 2x-y=7 \\ \end{matrix} \right.\)

\(\Leftrightarrow \left\{ \begin{matrix} 5x=10 \\ 2x-y=7 \\ \end{matrix} \right.\)(Cộng hai vế của hai phương trình)

\(\Leftrightarrow \left\{ \begin{matrix} x=2 \\ y=-3 \\ \end{matrix} \right.\)

Vậy HPT có nghiệm duy nhất \(\left( x;y \right)=\left( 2;-3 \right)\)

Trừ vế với vế của hai phương trình trong hệ, ta được:

Vậy hệ phương trình có nghiệm duy nhất là

Nhân hai vế của phương trình thứ hai với 2, rồi trừ vế với vế của hai phương trình trong hệ, ta được:

Vậy hệ phương trình có nghiệm duy nhất là (3; -2).

Nhân hai vế của phương trình thứ nhất với 3, nhân hai vế của phương trình thứ hai với 2, rồi trừ vế với vế của hai phương trình trong hệ, ta được

Vậy hệ phương trình có nghiệm duy nhất là (-1; 0).

e)

Nhân hai vế của phương trình thứ nhất với 5 rồi trừ vế với vế của hai phương trình trong hệ, ta được:

Vậy hệ phương trình có nghiệm duy nhất là (5; 3).

Bài 21 trang 18 SGK Toán 9 tập 2

Giải các hệ phương trình sau bằng phương pháp cộng đại số.

Hướng dẫn giải:

a) Nhân cả hai vế của phương trình thứ nhất với -\sqrt 2, rồi cộng từng vế hai phương trình, ta được:

Vậy hệ phương trình đã cho có nghiệm duy nhất là:

b) Nhân hai vế của phương trình thứ nhất với , rồi cộng từng vế hai phương trình.

Ta có

Suy ra

Vậy hệ phương trình đã cho có nghiệm duy nhất là

Bài 22 trang 19 SGK Toán 9 tập 2

Giải các hệ phương trình sau bằng phương pháp cộng đại số:

Hướng dẫn giải:

Nhân phương trình trên với 3, nhân phương trình dưới với 2, rồi cộng vế với vế của hai phương trình trong hệ, ta được:

Vậy hệ đã cho có nghiệm duy nhất là

Nhân hai vế phương trình trên với 2 rồi cộng hai vế của hai phương trình với nhau, ta được:

Vậy hệ phương trình vô nghiệm.

Đổi hỗn số về phân số rồi nhân hai vế của phương trình dưới với 3 sau đó trừ vế với vế của hai phương trình ta được:

Vậy hệ phương trình có vô số nghiệm.

Bài 23 trang 19 SGK Toán 9 tập 2

Giải hệ phương trình sau:

Hướng dẫn giải:

Xét hệ

Trừ từng vế hai phương trình (1) cho (2), ta được:

Thay (3) vào (1) ta được:

Vậy hệ phương trình đã cho có nghiệm duy nhất là:

Bài 24 trang 19 SGK Toán 9 tập 2

Giải hệ các phương trình:

a)

Hướng dẫn giải:

a)

Thực hiện nhân phá ngoặc và thu gọn, ta được:

Trừ vế với vế của hai phương trình ta được:

Vậy hệ đã cho có nghiệm duy nhất là

Phá ngoặc và thu gọn vế trái của hai phương trình trong hệ, ta được:

Vậy hệ phương trình đã cho có nghiệm duy nhất là (1; -1).

Bài 25 trang 19 SGK Toán 9 tập 2

Ta biết rằng: Một đa thức bằng đa thức 0 khi và chỉ khi tất cả các hệ số của nó bằng 0. Hãy tìm các giá trị của m và n để đa thức sau (với biến số x) bằng đa thức 0:

P(x) = (3m - 5n + 1)x + (4m - n -10).

Hướng dẫn giải:

Ta có

P(x) = (3m - 5n + 1)x + (4m - n -10) có hai hệ số là a=(3m - 5n + 1) và b=(4m - n -10).

Do đó

Vậy m=3, n=2 thì đa thức P(x) =0.

Bài 26 trang 19 SGK Toán 9 tập 2

Xác định a và b để đồ thị của hàm số y = ax + b đi qua điểm A và B trong mỗi trường hợp sau:

a)A(2; -2) và B(-1; 3)

b) A(-4; -2) và B(2; 1)

c) A(3; -1) và B(-3; 2)

d) và B(0; 2)

Hướng dẫn giải:

a)A(2; -2) và B(-1; 3)

Hàm số y=ax+b (1)

Vì đồ thị hàm số đi qua A(2; -2), thay x=2, y=-2 vào (1), ta được: -2=2a + b.

Vì đồ thị hàm số đi qua B(-1; 3), thay x=-1, y=3 vào (1), ta được: 3=-a + b.

Ta có hệ phương trình ẩn là a và b.

Vậy

b) A(-4; -2) và B(2; 1)

Hàm số y=ax+b (1)

Vì đồ thị hàm số đi qua A(-4; -2), thay x=-4,\ y=-2 vào (1), ta được: -2=-4a + b .

Vì đồ thị hàm số đi qua B(2; 1), thay x=2, y=1 vào (1), ta được: 1=2a + b.

Ta có hệ phương trình ẩn là a, b:

Vậy

c) A(3; -1) và B(-3; 2)

Hàm số y=ax+b (1)

Vì đồ thị hàm số đi qua A(3; -1), thay x=3, y=-1 vào (1), ta được: -1=3a + b

Vì đồ thị hàm số đi qua B(-3; 2), thay x=-3,y=2 vào (1), ta được: 2=-3a + b.

Ta có hệ phương trình ẩn a, b:

Vậy

d) và B(0; 2)

Hàm số y=ax+b (1)

Vì đồ thị hàm số đi qua , thay y=2 vào (1), ta được: .

Vì đồ thị hàm số đi qua B(0; 2), thay x=0, y=2 vào (1), ta được: 2= 0 . a + b .

Ta có hệ phương trình ẩn là a, b.

Vậy a=0, b=2.

Bài 27 trang 20 SGK Toán 9 tập 2

Bằng cách đặt ẩn phụ (theo hướng dẫn), đưa các hệ phương trình sau về dạng hệ hai phương trình bậc nhật hai ẩn rồi giải:

a)

Hướng dẫn.

Đặt

Hướng dẫn. Đặt

Hướng dẫn giải:

a) Điền kiện x ≠ 0, y ≠ 0.

Đặt (với ).

Phương trình đã cho trở thành:

Suy ra

Vậy hệ đã cho có nghiệm duy nhất

Hướng dẫn. Đặt

Điều kiện

Đặt (với ).

Phương trình đã cho trở thành:

Suy ra

Vậy hệ đã cho có nghiệm duy nhất

Bài 30 trang 22 SGK Toán 9 tập 2

Một ô tô đi từ A và dự định đến B lúc 12 giờ trưa. Nếu xe chạy với vận tốc 35 km/h

Đề bài

Một ô tô đi từ A và dự định đến B lúc 12 giờ trưa. Nếu xe chạy với vận tốc 35 km/h thì sẽ đến B chậm 2 giờ so với quy định. Nếu xe chạy với vận tốc 50 km/h thì sẽ đến B sớm 1 giờ so với quy định. Tính độ dài quãng đường AB và thời điểm xuất phát của ôtô tại A.

Sử dụng công thức: \(S=v.t\), trong đó \(S\) là quãng đường đi được (km); \(v\) là vận tốc (km/h); \(t\) là thời gian (h).

Lời giải chi tiết

Gọi \(x\) (km) là độ dài quãng đường \(AB\), \(y\) (giờ) là thời gian dự định đi từ \(A\) để đến \(B\) đúng lúc 12 giờ trưa. Điều kiện \(x > 0, y > 1\) (do ôtô đến \(B\) sớm hơn \(1\) giờ).

+) Trường hợp 1:

Xe đi với vận tốc 35 km (h)

Xe đến B chậm hơn 2 giờ nên thời gian đi hết là: \(y+2\) (giờ)

Quãng đường đi được là: \(35(y+2)\) (km)

Vì quãng đường không đổi nên ta có phương trình: \(x=35(y+2)\) (1)

+) Trường hợp 2:

Xe đi với vận tốc: 50 km/h

Vì xe đến B sớm hơn 1 giờ nên thời gian đi hết là: \(y-1\) (giờ)

Quãng đường đi được là: \(50(y-1)\) (km)

Vì quãng đường không đổi nên ta có phương trình: \(x=50(y-1)\) (2)

Từ (1) và (2) ta có hệ phương trình:

\(\left\{\begin{matrix} x = 35(y + 2) & & \\ x = 50(y - 1) & & \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} x = 35y + 70 & & \\ x = 50y - 50 & & \end{matrix}\right.\)

\(\Leftrightarrow \left\{\begin{matrix} x-35y=70 \ (1) \\ x- 50y=-50 \ (2) \end{matrix}\right.\)

Lấy vế trừ vế của (1) cho (2), ta được:

\(\left\{\begin{matrix} 15y=120 \\ x-50y=-50 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} y=8 \\ x=-50+50y \end{matrix}\right.\)

\(\left\{\begin{matrix} y=8 \\ x=-50+50.8 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} y=8 \\ x=350 \end{matrix}\right.\) (thỏa mãn)

Vậy quãng đường AB là 350km.

Thời điểm xuất phát của ô tô tại AA là: 12 − 8 = 412 − 8 = 4 giờ.

Trắc nghiệm Toán 9 bài 4

....................................

Ngoài Giải bài tập SGK Toán lớp 9 bài 4: Giải hệ phương trình bằng phương pháp cộng đại số. Mời các bạn học sinh còn có thể tham khảo các đề thi học học kì 1 lớp 9, đề thi học học kì 2 lớp 9 mà chúng tôi đã sưu tầm và chọn lọc. Với đề thi học kì 2 lớp 9 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt.