Giải Toán 9: Ôn tập Chương I – Hệ thức lượng giác trong tam giác vuông

Giải SGK Toán 9 bài: Ôn tập Chương I – Hệ thức lượng giác trong tam giác vuông.  hướng dẫn các bạn học sinh trả lời các câu hỏi trong sách giáo khoa môn Toán lớp 9. Với hướng dẫn giải chi tiết giúp các em học sinh có thêm tài liệu tham khảo, so sánh đánh giá kết quả, từ đó học tốt môn Toán lớp 9. Dưới đây là chi tiết bài tập, các em tham khảo nhé.

Câu hỏi 1 (trang 91 SGK Toán 9 Tập 1)

Cho hình 36. Hãy viết hệ thức giữa:

a) Cạnh huyền, cạnh góc vuông và hình chiếu của nó trên cạnh huyền.

b) Các cạnh góc vuông p, r và đường cao h.

c) Đường cao h và hình chiếu của các cạnh góc vuông trên cạnh huyền p', r'

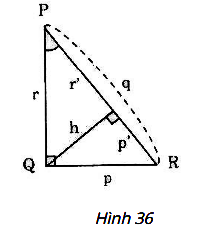
Hình 36

Trả lời:

a. p²= p'.q

r² = r'.q

b. \(\frac{1}{{{h^2}}} = \frac{1}{{{p^2}}} + \frac{1}{{{r^2}}}\)

c. h²= p'.r'

Câu hỏi 2 (trang 91 SGK Toán 9 Tập 1)

Cho hình 37.

a) Hãy viết công thức tính các tỉ số lượng giác của góc α

b) Hãy viết hệ thức giữa các tỉ số lượng giác của góc α và các tỉ số lượng giác của góc β.

Trả lời:

 a. \(\sin \alpha = \frac{b}{a};\cos \alpha = \frac{c}{a};\tan \alpha = \frac{b}{c};\cot \alpha = \frac{c}{b}\)

b) sin α = cos β; cos α = sin β

tg α = cotg β; cotg α = tgβ

Câu hỏi 3 (trang 91-92 SGK Toán 9 Tập 1)

Xem hình 37.

a) Hãy viết công thức tính các cạnh góc vuông b và c theo cạnh huyền a và tỉ số lượng giác của các góc α, β.

b) Hãy viết công thức tính mỗi cạnh góc vuông theo cạnh góc vuông kia và tỉ số lượng giác của các góc α, β.

Trả lời:

a) b = asin α = acosβ; c = asinβ = acosα

b) b = c.tgβ = c.cotgα

Câu hỏi 4 (trang 92 SGK Toán 9 Tập 1)

Để giải một tam giác vuông, cần biết ít nhất mấy góc và cạnh? Có lưu ý gì về số cạnh?

Trả lời:

Để giải một tam giác vuông cần biết hai yếu tố trong đó có ít nhất là một yếu tố cạnh

Bài 33 (trang 93 SGK Toán 9 Tập 1)

Chọn kết quả đúng trong các kết quả dưới đây:

a. Trong hình 41, sinα bằng

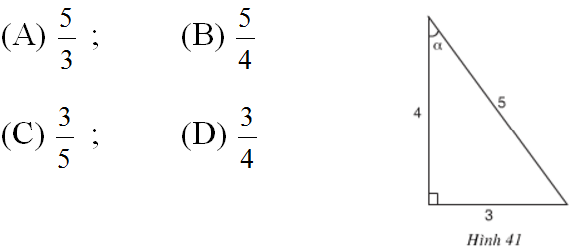
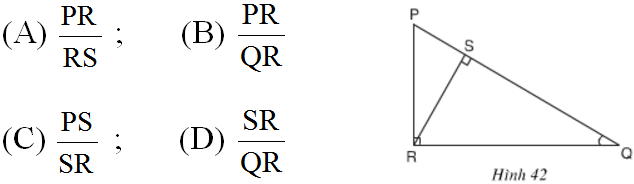
B. Trong hình 42, sin Q bằng

c. Trong hình 43, cos 30° bằng

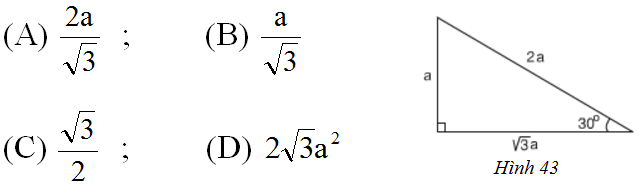
Lời giải:

a. Ta có:\(\displaystyle\sin \alpha = \dfrac{3}{5}.\)

Chọn (C)

b.

Xét \(\displaystyle\Delta QPR\) vuông tại R ta có: \(\displaystyle\sin Q = \dfrac{PR}{PQ}.\)

Xét \(\displaystyle\Delta RQS\) vuông tại S ta có: \(\displaystyle\sin Q = \dfrac{RS}{RQ}.\)

Chọn (D)

c. Chọn (C) vì: \(\displaystyle\cos {30^0} = {{\sqrt 3 a} \over {2a}} = {{\sqrt 3 } \over {2}}.\)

Bài 34 (trang 93 SGK Toán 9 Tập 1)

a) Trong hình 44, hệ thức nào trong các hệ thức sau là đúng?

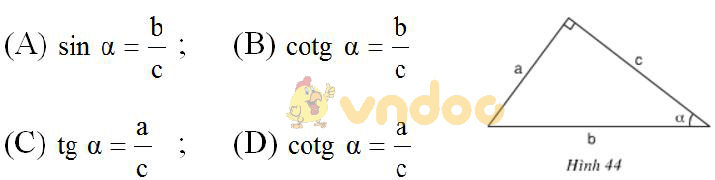
b) Trog hình 45, hệ thức nào trong các hệ thức sau không đúng?

(A) sin²α + cos²α = 1

(B) sin α = cos β

(C) cos β = sin (90^o – α)

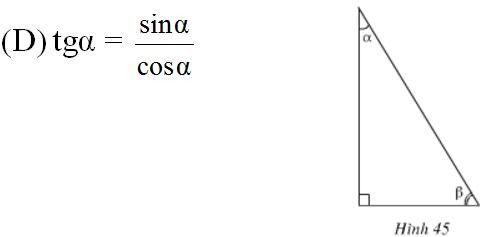
Lời giải:

a) Chọn C

b) Chọn C sai

- Vì đẳng thức đúng phải là: cos β = sin(90^o - β)

Bài 35 (trang 94 SGK Toán 9 Tập 1)

Tỉ số giữa hai cạnh góc vuông của một tam giác vuông bằng 19: 28. Tìm các góc của nó.

Lời giải:

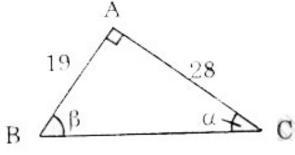
Kí hiệu góc như trên hình vẽ.

Tỉ số giữa hai cạnh góc vuông của một tam giác vuông là tg của góc nhọn này và là cotg của góc nhọn kia.

Giả sử α là góc nhọn của tam giác vuông đó.

Ta có: \(tga=\ \frac{19}{28}\) ≈ 0,6786

=> α ≈ 34^o10'

=> β ≈ 90^o - 34^o10' = 55^o50'

(Lưu ý: Bạn cũng có thể sử dụng cotg để tính, nhưng cũng sẽ cho kết quả tương tự bởi vì tính chất lượng giác của 2 góc phụ nhau.)

Bài 36 (trang 94 SGK Toán 9 Tập 1)

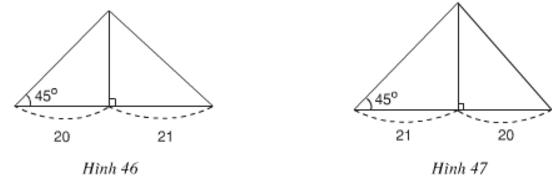
Cho tam giác có một góc bằng 45^o. Đường cao chia một cạnh kề với góc đó thành các phần 20cm và 21 cm. Tính cạnh lớn trong hai cạnh còn lại (lưu ý có hai trường hợp hình 46 và hình 47).

Lời giải:

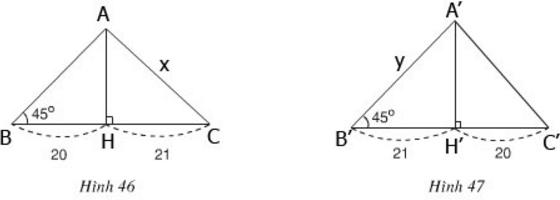
- Trường hợp hình 46: cạnh lớn trong hai cạnh còn lại được kí hiệu là x.

ΔHAB cân vì có ∠B = 45^o

=> HA = HB = 20

Áp dụng định lí Pitago trong ΔHAC có:

x² = AC² = HA² + HC² = 20² + 21² = 841

=> x = 29 hay độ dài cạnh lớn trong hai cạnh còn lại là 29.

- Trường hợp hình 47: cạnh lớn trong hai cạnh còn lại được kí hiệu là y.

ΔH'A'B' cân vì có ∠B' = 45^o

=> H'A' = H'B' = 21

Áp dụng định lí Pitago trong ΔH'A'B' có:

y² = A'B'² = H'A'² + H'B'² = 21² + 21² = 2.21²

=> y = 21√2 ≈ 29,7 hay độ dài cạnh lớn trong hai cạnh còn lại là 29,7.

Bài 37 (trang 94 SGK Toán 9 Tập 1)

Cho tam giác ABC có AB = 6cm, AC = 4,5cm, BC = 7,5cm.

a) Chứng minh tam giác ABC vuông tại A. Tính các góc B, C và đường cao AH của tam giác đó.

b) Hỏi rằng điểm M mà diện tích tam giác MBC bằng diện tích tam giác ABC nằm trên đường nào?

Lời giải:

a) Ta có: \(AB^2+AC^2={6^2} + 4,{5^2} = 36 + 20,25 = 56,25 = 7,{5^2}=BC^2.\)

⇒ ∆ABC có \(AB^2+AC^2=BC^2(=56,25)\) nên vuông tại A (định lý Pi-ta-go đảo).

\(\eqalign{&Ta \, \, có: tan B = {{AC} \over {AB}} = {{4,5} \over 6} = 0,75 \Rightarrow \widehat B \approx {37^0} \cr & \Rightarrow \widehat C = {90^0} - \widehat B = {53^0}. \cr}\)

Xét ∆ABC vuông tại A, AH là đường cao nên:

AH.BC = AB.AC

\(\displaystyle \Rightarrow AH = {{AB.AC} \over {BC}} = {{4,5.6} \over {7,5}} = 3,6(cm).\)

b)

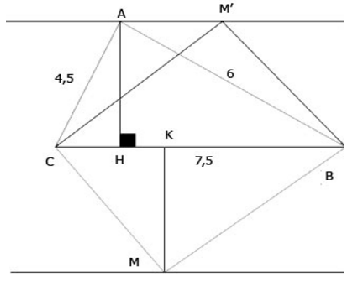
Kẻ MK \(\bot\) BC tại K.

Ta có: \(S_{ABC}=\dfrac{1}{2}AH.BC\)

\(S_{MBC}=\dfrac{1}{2}MK.BC\)

Từ đó, \(S_{ABC}=S_{MBC} \Leftrightarrow MK= AH=3,6cm.\)

Do đó M nằm trên hai đường thẳng song song cách BC một khoảng bằng 3,6 cm (hình vẽ).

Bài 38 (trang 95 SGK Toán 9 Tập 1)

Hai chiếc thuyền A và B ở vị trí được minh họa như trong hình 48. Tính khoảng cách giữa chúng (làm tròn đến mét).

Lời giải:

Trong tam giác vuông BIK có:

IB = IK.tg ∠IKB = IK.tg(50^o + 15^o) = 380.tg 65^o ≈ 814 (m)

Trong tam giác vuông AIK có:

IA = IK.tg ∠IKA = IK.tg 50^o = 380.tg50^o ≈ 452 (m)

Vậy khoảng cách giữa hai thuyền là:

AB = IB – IA = 814 – 452 = 362 (m)

Bài 39 (trang 95 SGK Toán 9 Tập 1)

Tìm khoảng cách giữa hai cọc để căng dây vượt qua vực trong hình 49 (làm tròn đến mét)

Hình 49

Lời giải:

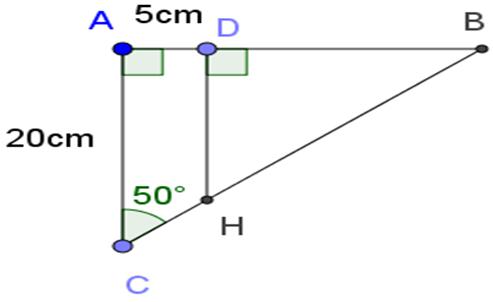
Kí hiệu như hình vẽ. Theo hệ thức giữa cạnh và góc của tam giác vuông:

Trong tam giác vuông ABC:

AB = AC tan 50^o = 20.tan 50^o = 23,83 m

=> BD = 20tan50^o - 5 = 18,83 m

 Trong tam giác vuông BHD: \(\Rightarrow BH = \frac{{BD}}{{\sin {{50}^0}}} = \frac{{18,83}}{{\sin {{50}^0}}} \approx 24,59\left( m \right)\)

Vậy khoảnh cách giữa hai cọc là 24,59 m.

Bài 40 (trang 95 SGK Toán 9 Tập 1)

Tính chiều cao của cây trong hình 50 (làm tròn đến đề-xi-mét)

Hình 50

Lời giải:

Kí hiệu như hình vẽ.

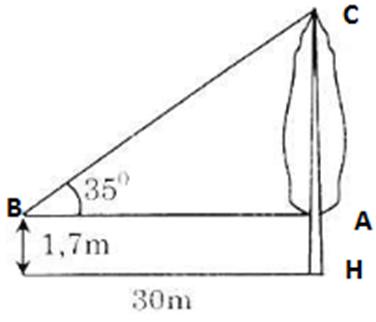
Trong tam giác vuông ABC có:

BA = AC.tg35^o = 30.tg35^o ≈ 21 (m)

Chiều cao của cây là:

BH = BA + AH ≈ 21 + 1,7 ≈ 22,7 (m)

Vậy chiều cao của cây là 22,7 (m).

(Ghi chú: Bạn cũng có thể làm tắt hơn như sau:

Chiều cao của cây là:

BH = BA + AH = AC.tg35^o + AH = 30.tg35^o + 1,7 = 22,7 m)

Bài 41 (trang 96 SGK Toán 9 Tập 1)

Tam giác ABC vuông tại C có AC = 2cm, BC = 5cm, ∠BAC = x, ∠ABC = y. Dùng các thông tin sau (nếu cần) để tìm x – y:

sin23^o36' ≈ 0,4

cos66^o24' ≈ 0,4

tg21^o48' ≈ 0,4

Lời giải:

 Ta có: \(\tan {21^0}48' = 0,4 = \frac{2}{5} = \frac{{AC}}{{BC}} = \tan \widehat B\)

Suy ra y = 21^o48'

=> x = 90^o - y = 68^o12' (x, y là hai góc phụ nhau)

Vậy x – y = 68^o12' - 21^o48' = 46^o24'

Bài 42 (trang 96 SGK Toán 9 Tập 1)

Ở một cái thang dài 3m người ta ghi: "Để đảm bảo an toàn khi dùng thang, phải đặt thang này tạo với mặt đất một góc có độ lớn từ 60^o đến 70^o". Đo góc thì khó hơn đo độ dài. Vậy hãy cho biết: Khi dùng thang đó chân thang phải đặt cách tường khoảng bao nhiêu mét để đảm bảo an toàn?

Lời giải:

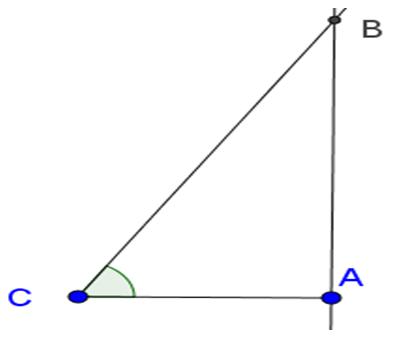
Kí hiệu như hình vẽ.

Trong tam giác vuông ABC có:

AC = BC.cosC = 3.cosC

Vì phải đặt thang tạo với mặt đất một góc 60^o đến 70^o nên

60^o ≤ ∠C ≤ 70^o

=> cos 70^o ≤ cosC ≤ cos 60^o

=> 3.cos 70^o ≤ 3.cosC ≤ 3.cos 60^o

=> 1,03 ≤ AC ≤ 1,5

Vậy phải đặt chân thang cách tường từ 1,03 m đến 1,5 m.

Bài 43 (trang 96 SGK Toán 9 Tập 1): Đố

Vào khoảng năm 200 trước Công Nguyên, Ơratôxten, một nhà toán học và thiên văn học Hi Lạp, đã ước lượng được "chu vi" của Trái Đất (chu vi đường Xích Đạo) nhờ hai quan sát sau:

1) Một ngày trong năm, ông ta để ý thấy Mặt Trời chiếu thẳng các đáy giếng ở thành phố Xy-en (nay gọi là At-xu-an), tức là tia sáng chiếu thẳng đứng.

2) Cùng lúc đó ở thành phố A-lếch-xăng-đri-a cách Xy-en 800km, một tháp cao 25m có bóng trên mặt đất dài 3,1m.

Từ hai quan sát trên, em hãy tính xấp xỉ "chu vi" của Trái Đất.

(Trên hình 51 điểm S tượng trưng cho thành phố Xy-en, điểm A tượng trưng cho thành phố A-lếch-xăng-đri-a, bóng của tháp trên mặt đất được coi là đoạn thẳng AB).

Hình 51

Lời giải:

Gọi c là chu vi Trái đất, góc ∠AOS = α. Ta có: \(c = AS.\frac{{{{360}^0}}}{\alpha } = 800.\frac{{{{360}^0}}}{\alpha }\)

Vì các tia sáng chiếu thẳng đứng nên BC // SO do đó:

\(\widehat {AOS} = \widehat {ACB}\) (so le trong)

Trong tam giác ABC vuông tại A có:

\(\begin{matrix} \tan \widehat C = \dfrac{{AB}}{{AC}} = \dfrac{{3,1}}{{25}} \approx 0,124 \Rightarrow \widehat C \approx 7,{07^0} \hfill \\ {\text{Do }}\widehat {AOS} = \widehat {ACB} \Rightarrow \alpha = 7,{07^0} \hfill \\ \end{matrix}\)

Vậy chu vi Trái đất là: \(c = 800.\frac{{{{360}^0}}}{{7,{{07}^0}}} \approx 40736\left( {km} \right)\)

..................................................

Như vậy VnDoc đã giới thiệu các bạn tài liệu Giải bài tập Toán 9 bài: Ôn tập Chương I – Hệ thức lượng giác trong tam giác vuông. Để tham khảo lời giải những bài tiếp theo, mời các em vào chuyên mục Giải Toán 9 trên VnDoc nhé. Chuyên mục tổng hợp lời giải theo từng đơn vị bài học giúp các em nắm vững kiến thức được học trong SGK Toán 9. Chúc các em học tốt, nếu có thắc mắc hay trao đổi kiến thức các em có thể vào link sau nhé: Hỏi - đáp.

Ngoài tài liệu trên, mời các bạn tham khảo thêm Tài liệu học tập lớp 9, và các đề học kì 1 lớp 9 và đề thi học kì 2 lớp 9 mới nhất được cập nhật.

Bài tiếp theo: Giải Toán 9 bài 1: Sự xác định đường tròn. Tính chất đối xứng của đường tròn