VnDoc.com

Giải Toán 9 bài 4 Liên hệ giữa phép chia và phép khai phương

Giải SGK Toán 9 trang 18, 19, 20

Bài trước

Tải về

Bài sau

Lớp: Lớp 9

Môn: Toán

Dạng tài liệu: Giải bài tập

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Giải SGK Toán 9 bài 4: Liên hệ giữa phép chia và phép khai phương giúp các em trả lời các câu hỏi trong SGK Toán 9 tập 1 trang 18, 19, 20. Với hướng dẫn giải chi tiết giúp các em học sinh có thêm tài liệu tham khảo, so sánh đánh giá kết quả, từ đó học tốt môn Toán lớp 9. Dưới đây là chi tiết bài tập, các em tham khảo nhé.

Giải Toán 9 bài 4: Liên hệ giữa phép chia và phép khai phương

A. Trả lời câu hỏi trang 16, 17, 18 SGK Toán 9 tập 1
B. Giải bài tập trang 18, 19, 20 sgk Toán 9 tập 1
C. Trắc nghiệm Toán 9 bài 4

A. Trả lời câu hỏi trang 16, 17, 18 SGK Toán 9 tập 1

Câu hỏi 1 trang 16 SGK Toán 9 tập 1

Tính và so sánh: $\sqrt {\frac{{16}}{{25}}}$ $\sqrt {\frac{{16}}{{25}}}$ và $\frac{{\sqrt {16} }}{{\sqrt {25} }}$ $\frac{{\sqrt {16} }}{{\sqrt {25} }}$

Hướng dẫn giải:

$\left\{ {\begin{array}{*{20}{c}} {\sqrt {\dfrac{{16}}{{25}}} = \sqrt {\dfrac{{{4^2}}}{{{5^2}}}} = \sqrt {{{\left( {\dfrac{4}{5}} \right)}^2}} = \dfrac{4}{5}} \\ {\dfrac{{\sqrt {16} }}{{\sqrt {25} }} = \dfrac{{\sqrt {{4^2}} }}{{\sqrt {{5^2}} }} = \dfrac{4}{5}} \end{array}} \right. \Rightarrow \sqrt {\dfrac{{16}}{{25}}} = \dfrac{{\sqrt {16} }}{{\sqrt {25} }}$ $\left\{ {\begin{array}{*{20}{c}} {\sqrt {\dfrac{{16}}{{25}}} = \sqrt {\dfrac{{{4^2}}}{{{5^2}}}} = \sqrt {{{\left( {\dfrac{4}{5}} \right)}^2}} = \dfrac{4}{5}} \\ {\dfrac{{\sqrt {16} }}{{\sqrt {25} }} = \dfrac{{\sqrt {{4^2}} }}{{\sqrt {{5^2}} }} = \dfrac{4}{5}} \end{array}} \right. \Rightarrow \sqrt {\dfrac{{16}}{{25}}} = \dfrac{{\sqrt {16} }}{{\sqrt {25} }}$

Câu hỏi 2 trang 17 SGK Toán 9 tập 1

Tính:

a. $\sqrt {\frac{{225}}{{256}}}$ $\sqrt {\frac{{225}}{{256}}}$

b. $\sqrt {0,0196}$ $\sqrt {0,0196}$

Hướng dẫn giải:

a. $\sqrt {\frac{{225}}{{256}}} = \sqrt {\frac{{{{15}^2}}}{{{{16}^2}}}} = \sqrt {{{\left( {\frac{{15}}{{16}}} \right)}^2}} = \frac{{15}}{{16}}$ $\sqrt {\frac{{225}}{{256}}} = \sqrt {\frac{{{{15}^2}}}{{{{16}^2}}}} = \sqrt {{{\left( {\frac{{15}}{{16}}} \right)}^2}} = \frac{{15}}{{16}}$

b. $\sqrt {0,0196} = \sqrt {\frac{{196}}{{10000}}} = \sqrt {\frac{{{{14}^2}}}{{{{100}^2}}}} = \sqrt {{{\left( {\frac{{14}}{{100}}} \right)}^2}} = \frac{{14}}{{100}} = 0,14$ $\sqrt {0,0196} = \sqrt {\frac{{196}}{{10000}}} = \sqrt {\frac{{{{14}^2}}}{{{{100}^2}}}} = \sqrt {{{\left( {\frac{{14}}{{100}}} \right)}^2}} = \frac{{14}}{{100}} = 0,14$

Câu hỏi 3 trang 18 SGK Toán 9 tập 1

Tính:

a. $\frac{{\sqrt {999} }}{{\sqrt {111} }}$ $\frac{{\sqrt {999} }}{{\sqrt {111} }}$

b. $\frac{{\sqrt {52} }}{{\sqrt {117} }}$ $\frac{{\sqrt {52} }}{{\sqrt {117} }}$

Hướng dẫn giải:

a. $\frac{{\sqrt {999} }}{{\sqrt {111} }} = \sqrt {\frac{{999}}{{111}}} = \sqrt 9 = 3$ $\frac{{\sqrt {999} }}{{\sqrt {111} }} = \sqrt {\frac{{999}}{{111}}} = \sqrt 9 = 3$

b. $\frac{{\sqrt {52} }}{{\sqrt {117} }} = \sqrt {\frac{{52}}{{117}}} = \sqrt {\frac{4}{9}} = \frac{2}{3}$ $\frac{{\sqrt {52} }}{{\sqrt {117} }} = \sqrt {\frac{{52}}{{117}}} = \sqrt {\frac{4}{9}} = \frac{2}{3}$

Câu hỏi 3 trang 18 SGK Toán 9 tập 1

Rút gọn:

a. $\sqrt {\frac{{2{a^2}{b^4}}}{{50}}}$ $\sqrt {\frac{{2{a^2}{b^4}}}{{50}}}$ b. $\frac{{\sqrt {2a{b^2}} }}{{\sqrt {162} }}$ $\frac{{\sqrt {2a{b^2}} }}{{\sqrt {162} }}$ với $a \geqslant 0$ $a \geqslant 0$

Hướng dẫn giải:

a. $\sqrt {\frac{{2{a^2}{b^4}}}{{50}}} = \sqrt {\frac{{{a^2}{{\left( {{b^2}} \right)}^2}}}{{25}}} = \sqrt {{{\left( {\frac{{a{b^2}}}{5}} \right)}^2}} = \frac{{\left| a \right|.{b^2}}}{5}$ $\sqrt {\frac{{2{a^2}{b^4}}}{{50}}} = \sqrt {\frac{{{a^2}{{\left( {{b^2}} \right)}^2}}}{{25}}} = \sqrt {{{\left( {\frac{{a{b^2}}}{5}} \right)}^2}} = \frac{{\left| a \right|.{b^2}}}{5}$

Khi $a \geqslant 0 \Rightarrow \left| a \right| = a \Rightarrow \sqrt {\frac{{2{a^2}{b^4}}}{{50}}} = \frac{{a{b^2}}}{5}$ $a \geqslant 0 \Rightarrow \left| a \right| = a \Rightarrow \sqrt {\frac{{2{a^2}{b^4}}}{{50}}} = \frac{{a{b^2}}}{5}$

Khi $a < 0 \Rightarrow \left| a \right| = - a \Rightarrow \sqrt {\frac{{2{a^2}{b^4}}}{{50}}} = \frac{{ - a{b^2}}}{5}$ $a < 0 \Rightarrow \left| a \right| = - a \Rightarrow \sqrt {\frac{{2{a^2}{b^4}}}{{50}}} = \frac{{ - a{b^2}}}{5}$

B. Giải bài tập trang 18, 19, 20 sgk Toán 9 tập 1

Bài 28 trang 18 sgk Toán 9 tập 1

Tính

$a) \sqrt{\dfrac{289}{225}};$ $a) \sqrt{\dfrac{289}{225}};$ $b) \sqrt{2\dfrac{14}{25}};$ $b) \sqrt{2\dfrac{14}{25}};$

$c) \sqrt{\dfrac{0,25}{9}};$ $c) \sqrt{\dfrac{0,25}{9}};$ $d) \sqrt{\dfrac{8,1}{1,6}}.$ $d) \sqrt{\dfrac{8,1}{1,6}}.$

Hướng dẫn giải:

a) Ta có:

$\sqrt{\dfrac{289}{225}}=\dfrac{\sqrt{289}}{\sqrt{225}}=\dfrac{\sqrt {17^2}}{\sqrt{15^2}}=\dfrac{17}{15}.$ $\sqrt{\dfrac{289}{225}}=\dfrac{\sqrt{289}}{\sqrt{225}}=\dfrac{\sqrt {17^2}}{\sqrt{15^2}}=\dfrac{17}{15}.$

b) Ta có:

$\sqrt{2\dfrac{14}{25}}=\sqrt{\dfrac{2.25+14}{25}}=\sqrt{\dfrac{50+14}{25}}$ $\sqrt{2\dfrac{14}{25}}=\sqrt{\dfrac{2.25+14}{25}}=\sqrt{\dfrac{50+14}{25}}$

$=\sqrt{\dfrac{64}{25}}=\dfrac{\sqrt{64}}{\sqrt{25}}=\dfrac{\sqrt{8^2}}{\sqrt{5^2}}=\dfrac{8}{5}.$ $=\sqrt{\dfrac{64}{25}}=\dfrac{\sqrt{64}}{\sqrt{25}}=\dfrac{\sqrt{8^2}}{\sqrt{5^2}}=\dfrac{8}{5}.$

c) Ta có:

$\sqrt{\dfrac{0,25}{9}}=\dfrac{\sqrt{0,25}}{\sqrt{9}}=\dfrac{\sqrt{0,5^2}}{\sqrt{3^2}}=\dfrac{0,5}{3}$ $\sqrt{\dfrac{0,25}{9}}=\dfrac{\sqrt{0,25}}{\sqrt{9}}=\dfrac{\sqrt{0,5^2}}{\sqrt{3^2}}=\dfrac{0,5}{3}$

$=0,5.\dfrac{1}{3}=\dfrac{1}{2}.\dfrac{1}{3}=\dfrac{1}{6}.$ $=0,5.\dfrac{1}{3}=\dfrac{1}{2}.\dfrac{1}{3}=\dfrac{1}{6}.$

d) Ta có:

$\sqrt{\dfrac{8,1}{1,6}}=\sqrt{\dfrac{81.0,1}{16.0,1}}=\sqrt{\dfrac{81}{16}}=\dfrac{\sqrt{81}}{\sqrt{16}}=\dfrac{\sqrt{9^2}}{\sqrt{4^2}}=\dfrac{9}{4}.$ $\sqrt{\dfrac{8,1}{1,6}}=\sqrt{\dfrac{81.0,1}{16.0,1}}=\sqrt{\dfrac{81}{16}}=\dfrac{\sqrt{81}}{\sqrt{16}}=\dfrac{\sqrt{9^2}}{\sqrt{4^2}}=\dfrac{9}{4}.$

Bài 29 trang 19 sgk Toán 9 tập 1

Tính

$a) \dfrac{\sqrt{2}}{\sqrt{18}};$ $a) \dfrac{\sqrt{2}}{\sqrt{18}};$ $b) \dfrac{\sqrt{15}}{\sqrt{735}};$ $b) \dfrac{\sqrt{15}}{\sqrt{735}};$

$c) \dfrac{\sqrt{12500}}{\sqrt{500}};$ $c) \dfrac{\sqrt{12500}}{\sqrt{500}};$ $d) \dfrac{\sqrt{6^{5}}}{\sqrt{2^{3}.3^{5}}}.$ $d) \dfrac{\sqrt{6^{5}}}{\sqrt{2^{3}.3^{5}}}.$

Hướng dẫn giải:

$a) \dfrac{\sqrt{2}}{\sqrt{18}}=\sqrt{\dfrac{2}{18}}=\sqrt{\dfrac{2.1}{2.9}}=\sqrt{\dfrac{1}{9}}=\sqrt {{{\left( {\dfrac{1}{3}} \right)}^2}} =\dfrac{1}{3}.$ $a) \dfrac{\sqrt{2}}{\sqrt{18}}=\sqrt{\dfrac{2}{18}}=\sqrt{\dfrac{2.1}{2.9}}=\sqrt{\dfrac{1}{9}}=\sqrt {{{\left( {\dfrac{1}{3}} \right)}^2}} =\dfrac{1}{3}.$

$b) \dfrac{\sqrt{15}}{\sqrt{735}}=\sqrt{\dfrac{15}{735}}=\sqrt{\dfrac{15.1}{15.49}}=\sqrt{\dfrac{1}{49}}=\sqrt {{{\left( {\dfrac{1}{7}} \right)}^2}}$ $b) \dfrac{\sqrt{15}}{\sqrt{735}}=\sqrt{\dfrac{15}{735}}=\sqrt{\dfrac{15.1}{15.49}}=\sqrt{\dfrac{1}{49}}=\sqrt {{{\left( {\dfrac{1}{7}} \right)}^2}}$

$=\dfrac{1}{7}.$ $=\dfrac{1}{7}.$

$c) \dfrac{\sqrt{12500}}{\sqrt{500}}=\sqrt{\dfrac{12500}{500}}=\sqrt{\dfrac{500.25}{500}}$ $c) \dfrac{\sqrt{12500}}{\sqrt{500}}=\sqrt{\dfrac{12500}{500}}=\sqrt{\dfrac{500.25}{500}}$

$=\sqrt{25}=\sqrt{5^2}=5.$ $=\sqrt{25}=\sqrt{5^2}=5.$

$d) \dfrac{\sqrt{6^{5}}}{\sqrt{2^{3}.3^{5}}}=\sqrt{\dfrac{6^5}{2^3.3^5}}=\sqrt{\dfrac{(2.3)^5}{2^3.3^5}}=\sqrt{\dfrac{2^5.3^5}{2^3.3^5}}$ $d) \dfrac{\sqrt{6^{5}}}{\sqrt{2^{3}.3^{5}}}=\sqrt{\dfrac{6^5}{2^3.3^5}}=\sqrt{\dfrac{(2.3)^5}{2^3.3^5}}=\sqrt{\dfrac{2^5.3^5}{2^3.3^5}}$

$=\sqrt{\dfrac{2^5.3^5}{2^3.3^5}}=\sqrt{\dfrac{2^5}{2^3}}=\sqrt{\dfrac{2^3.2^2}{2^3}}=\sqrt{2^2}=2$ $=\sqrt{\dfrac{2^5.3^5}{2^3.3^5}}=\sqrt{\dfrac{2^5}{2^3}}=\sqrt{\dfrac{2^3.2^2}{2^3}}=\sqrt{2^2}=2$

Bài 30 trang 19 sgk Toán 9 tập 1

Rút gọn các biểu thức sau:

$a) \dfrac{y}{x}.\sqrt{\dfrac{x^{2}}{y^{4}}}$ $a) \dfrac{y}{x}.\sqrt{\dfrac{x^{2}}{y^{4}}}$ với $x > 0,\ y ≠ 0;$ $x > 0,\ y ≠ 0;$

$b) 2 y^{2}. \sqrt{\dfrac{x^{4}}{4y^{2}}}$ $b) 2 y^{2}. \sqrt{\dfrac{x^{4}}{4y^{2}}}$ với $y < 0;$

$c) 5xy. \sqrt{\dfrac{25x^{2}}{y^{6}}}$ $c) 5xy. \sqrt{\dfrac{25x^{2}}{y^{6}}}$ với $x < 0,\ y > 0;$ $x < 0,\ y > 0;$

$d) 0,2x^{3}y^{3}.\sqrt{\dfrac{16}{x^{4}y^{8}}}$ $d) 0,2x^{3}y^{3}.\sqrt{\dfrac{16}{x^{4}y^{8}}}$ với $x ≠ 0,\ y ≠ 0.$ $x ≠ 0,\ y ≠ 0.$

Hướng dẫn giải:

a) Ta có:

$\dfrac{y}{x}.\sqrt{\dfrac{x^{2}}{y^{4}}}=\dfrac{y}{x}.\dfrac{\sqrt{x^2}}{\sqrt{y^{4}}}$ $\dfrac{y}{x}.\sqrt{\dfrac{x^{2}}{y^{4}}}=\dfrac{y}{x}.\dfrac{\sqrt{x^2}}{\sqrt{y^{4}}}$

$=\dfrac{y}{x}.\dfrac{\sqrt{x^2}}{\sqrt{(y^2)^2}}=\dfrac{y}{x}.\dfrac{|x|}{|y^2|}$ $=\dfrac{y}{x}.\dfrac{\sqrt{x^2}}{\sqrt{(y^2)^2}}=\dfrac{y}{x}.\dfrac{|x|}{|y^2|}$

Vì $x> 0$ nên $|x|=x.$

Vì $y \ne 0$ $y \ne 0$ nên $y^2 > 0 \Rightarrow |y^2|=y^2.$ $y^2 > 0 \Rightarrow |y^2|=y^2.$

$\Rightarrow \dfrac{y}{x}.\dfrac{|x|}{|y^2|} =\dfrac{y}{x}.\dfrac{x}{y^2}=\dfrac{y}{x}.\dfrac{x}{y.y}=\dfrac{1}{y}.$ $\Rightarrow \dfrac{y}{x}.\dfrac{|x|}{|y^2|} =\dfrac{y}{x}.\dfrac{x}{y^2}=\dfrac{y}{x}.\dfrac{x}{y.y}=\dfrac{1}{y}.$

Vậy $\dfrac{y}{x}.\sqrt{\dfrac{x^{2}}{y^{4}}}=\dfrac{1}{y}.$ $\dfrac{y}{x}.\sqrt{\dfrac{x^{2}}{y^{4}}}=\dfrac{1}{y}.$

b) Ta có:

$2y^2.\sqrt{\dfrac{x^{4}}{4y^{2}}}=2y^2.\dfrac{\sqrt{x^4}}{\sqrt{4y^2}}=2y^2.\dfrac{\sqrt{(x^2)^2}}{\sqrt{2^2.y^2}}$ $2y^2.\sqrt{\dfrac{x^{4}}{4y^{2}}}=2y^2.\dfrac{\sqrt{x^4}}{\sqrt{4y^2}}=2y^2.\dfrac{\sqrt{(x^2)^2}}{\sqrt{2^2.y^2}}$

$=2y^2.\dfrac{\sqrt{(x^2)^2}}{\sqrt{(2y)^2}}=2y^2.\dfrac{|x^2|}{|2y|}$ $=2y^2.\dfrac{\sqrt{(x^2)^2}}{\sqrt{(2y)^2}}=2y^2.\dfrac{|x^2|}{|2y|}$

Vì $x^2 \ge 0 \Rightarrow |x^2|=x^2.$ $x^2 \ge 0 \Rightarrow |x^2|=x^2.$

Vì $y<0$ nên $2y < 0 \Rightarrow |2y|=-2y$ $2y < 0 \Rightarrow |2y|=-2y$

$\Rightarrow 2y^2.\dfrac{|x^2|}{|2y|}=2y^2.\dfrac{x^2}{-2y}=\dfrac{2y^2.x^2}{-2y}$ $\Rightarrow 2y^2.\dfrac{|x^2|}{|2y|}=2y^2.\dfrac{x^2}{-2y}=\dfrac{2y^2.x^2}{-2y}$

$=\dfrac{x^2.y.2y}{-2y}=-x^2y.$ $=\dfrac{x^2.y.2y}{-2y}=-x^2y.$

Vậy $2y^2.\sqrt{\dfrac{x^{4}}{4y^{2}}}=-x^2y.$ $2y^2.\sqrt{\dfrac{x^{4}}{4y^{2}}}=-x^2y.$

c) Ta có:

$5xy.\sqrt{\dfrac{25x^{2}}{y^{6}}}=5xy.\dfrac{\sqrt{25x^2}}{\sqrt{y^6}}=\dfrac{\sqrt{5^2.x^2}}{\sqrt{(y^3)^2}}$ $5xy.\sqrt{\dfrac{25x^{2}}{y^{6}}}=5xy.\dfrac{\sqrt{25x^2}}{\sqrt{y^6}}=\dfrac{\sqrt{5^2.x^2}}{\sqrt{(y^3)^2}}$

$=\dfrac{\sqrt{(5x)^2}}{\sqrt{(y^3)^2}}=5xy.\dfrac{|5x|}{|y^3|}$ $=\dfrac{\sqrt{(5x)^2}}{\sqrt{(y^3)^2}}=5xy.\dfrac{|5x|}{|y^3|}$

Vì $x<0 \Rightarrow |5x| = - 5x$ $x<0 \Rightarrow |5x| = - 5x$

Vì $y>0 \Rightarrow y^3 >0 \Rightarrow |y^3|=y^3.$ $y>0 \Rightarrow y^3 >0 \Rightarrow |y^3|=y^3.$

$\Rightarrow 5xy.\dfrac{|5x|}{|y^3|}=5xy.\dfrac{-5x}{y^3}=\dfrac{5xy.(-5x)}{y^3}$ $\Rightarrow 5xy.\dfrac{|5x|}{|y^3|}=5xy.\dfrac{-5x}{y^3}=\dfrac{5xy.(-5x)}{y^3}$

$=\dfrac{[5.(-5)].(x.x).y}{y^2.y}=\dfrac{-25x^2}{y^2}$ $=\dfrac{[5.(-5)].(x.x).y}{y^2.y}=\dfrac{-25x^2}{y^2}$

Vậy $5xy.\sqrt{\dfrac{25x^{2}}{y^{6}}}=\dfrac{-25x^2}{y^2}.$ $5xy.\sqrt{\dfrac{25x^{2}}{y^{6}}}=\dfrac{-25x^2}{y^2}.$

d) Ta có:

$0,2x^{3}y^{3}.\sqrt{\dfrac{16}{x^{4}y^{8}}}=0,2x^3y^3.\dfrac{\sqrt{16}}{\sqrt{x^4y^8}}$ $0,2x^{3}y^{3}.\sqrt{\dfrac{16}{x^{4}y^{8}}}=0,2x^3y^3.\dfrac{\sqrt{16}}{\sqrt{x^4y^8}}$

$=0,2x^3y^3\dfrac{\sqrt{4^2}}{\sqrt{(x^2)^2.(y^4)^2}}$ $=0,2x^3y^3\dfrac{\sqrt{4^2}}{\sqrt{(x^2)^2.(y^4)^2}}$

$=0,2x^3y^3.\dfrac{\sqrt{4^2}}{\sqrt{(x^2)^2}.\sqrt{(y^4)^2}}=0,2x^3y^3.\dfrac{4}{|x^2|.|y^4|}.$ $=0,2x^3y^3.\dfrac{\sqrt{4^2}}{\sqrt{(x^2)^2}.\sqrt{(y^4)^2}}=0,2x^3y^3.\dfrac{4}{|x^2|.|y^4|}.$

Bài 31 trang 19 sgk Toán 9 tập 1

Đề bài

a) So sánh $\sqrt{25 - 16}$ $\sqrt{25 - 16}$ và $\sqrt {25} - \sqrt {16};$ $\sqrt {25} - \sqrt {16};$

b) Chứng minh rằng: với $a > b >0$ thì $\sqrt a - \sqrt b < \sqrt {a - b} .$ $\sqrt a - \sqrt b < \sqrt {a - b} .$

Hướng dẫn giải:

a) Ta có:

$+) \sqrt {25 - 16} = \sqrt 9 =\sqrt{3^2}= 3.$ $+) \sqrt {25 - 16} = \sqrt 9 =\sqrt{3^2}= 3.$
$+) \sqrt {25} - \sqrt {16} = \sqrt{5^2}-\sqrt{4^2}=5 - 4 = 1 .$ $+) \sqrt {25} - \sqrt {16} = \sqrt{5^2}-\sqrt{4^2}=5 - 4 = 1 .$

Vì $3>1 \Leftrightarrow \sqrt {25 - 16}>\sqrt {25} - \sqrt {16} .$ $3>1 \Leftrightarrow \sqrt {25 - 16}>\sqrt {25} - \sqrt {16} .$

Vậy $\sqrt {25 - 16} > \sqrt {25} - \sqrt {16}$ $\sqrt {25 - 16} > \sqrt {25} - \sqrt {16}$

b Theo bài 26, ta đã chứng minh được: Với a>0 và b>0 thì:

$\sqrt{a+b}<\sqrt{a}+\sqrt{b}.$ $\sqrt{a+b}<\sqrt{a}+\sqrt{b}.$

Theo giải thiết, ta có

+) $b>0$

+) $a>b \Rightarrow a-b >0$ $a>b \Rightarrow a-b >0$

Áp dụng bài 26 cho hai số a-b và b, ta được:

$\sqrt{(a-b) +b}< \sqrt{a-b}+\sqrt{b}$ $\sqrt{(a-b) +b}< \sqrt{a-b}+\sqrt{b}$

$\Leftrightarrow \sqrt{a-b+b} < \sqrt{a-b} +\sqrt{b}$ $\Leftrightarrow \sqrt{a-b+b} < \sqrt{a-b} +\sqrt{b}$

$\Leftrightarrow \sqrt a < \sqrt{a-b}+\sqrt b$ $\Leftrightarrow \sqrt a < \sqrt{a-b}+\sqrt b$

$\Leftrightarrow \sqrt a - \sqrt b < \sqrt{a-b} (đpcm).$ $\Leftrightarrow \sqrt a - \sqrt b < \sqrt{a-b} (đpcm).$

Bài 32 trang 19 sgk Toán 9 tập 1

Tính

$a) \sqrt{1\dfrac{9}{16}.5\dfrac{4}{9}.0,01};$ $a) \sqrt{1\dfrac{9}{16}.5\dfrac{4}{9}.0,01};$

$b) \sqrt{1,44.1,21-1,44.0,4};$ $b) \sqrt{1,44.1,21-1,44.0,4};$

$c) \sqrt{\dfrac{165^{2}-124^{2}}{164}};$ $c) \sqrt{\dfrac{165^{2}-124^{2}}{164}};$

$d) \sqrt{\dfrac{149^{2}-76^{2}}{457^{2}-384^{2}}}.$ $d) \sqrt{\dfrac{149^{2}-76^{2}}{457^{2}-384^{2}}}.$

a) Ta có:

$\sqrt{1\dfrac{9}{16}.5\dfrac{4}{9}.0,01}=\sqrt{\dfrac{1.16+9}{16}.\dfrac{5.9+4}{9}.\dfrac{1}{100}}$ $\sqrt{1\dfrac{9}{16}.5\dfrac{4}{9}.0,01}=\sqrt{\dfrac{1.16+9}{16}.\dfrac{5.9+4}{9}.\dfrac{1}{100}}$

$=\sqrt{\dfrac{16+9}{16}.\dfrac{45+4}{9}.\dfrac{1}{100}}$ $=\sqrt{\dfrac{16+9}{16}.\dfrac{45+4}{9}.\dfrac{1}{100}}$

$=\sqrt{\dfrac{25}{16}.\dfrac{49}{9}.\dfrac{1}{100}}$ $=\sqrt{\dfrac{25}{16}.\dfrac{49}{9}.\dfrac{1}{100}}$

$=\sqrt{\dfrac{25}{16}}.\sqrt{\dfrac{49}{9}}.\sqrt{\dfrac{1}{100}}$ $=\sqrt{\dfrac{25}{16}}.\sqrt{\dfrac{49}{9}}.\sqrt{\dfrac{1}{100}}$

$=\dfrac{\sqrt{25}}{\sqrt{16}}.\dfrac{\sqrt{49}}{\sqrt{9}}.\dfrac{\sqrt{1}}{\sqrt{100}}$ $=\dfrac{\sqrt{25}}{\sqrt{16}}.\dfrac{\sqrt{49}}{\sqrt{9}}.\dfrac{\sqrt{1}}{\sqrt{100}}$

$=\dfrac{\sqrt{5^2}}{\sqrt{4^2}}.\dfrac{\sqrt{7^2}}{\sqrt{3^2}}.\dfrac{1}{\sqrt{10^2}}$ $=\dfrac{\sqrt{5^2}}{\sqrt{4^2}}.\dfrac{\sqrt{7^2}}{\sqrt{3^2}}.\dfrac{1}{\sqrt{10^2}}$

$=\dfrac{5}{4}.\dfrac{7}{3}.\dfrac{1}{10}=\dfrac{5.7.1}{4.3.10}=\dfrac{35}{120}=\dfrac{7}{24}.$ $=\dfrac{5}{4}.\dfrac{7}{3}.\dfrac{1}{10}=\dfrac{5.7.1}{4.3.10}=\dfrac{35}{120}=\dfrac{7}{24}.$

b) Ta có:

$\sqrt{1,44.1,21-1,44.0,4} = \sqrt{1,44(1,21-0,4)}$ $\sqrt{1,44.1,21-1,44.0,4} = \sqrt{1,44(1,21-0,4)}$

$=\sqrt{1,44.0,81}$ $=\sqrt{1,44.0,81}$

$=\sqrt{1,44}.\sqrt{0,81}$ $=\sqrt{1,44}.\sqrt{0,81}$

$=\sqrt{1,2^2}.\sqrt{0,9^2}$ $=\sqrt{1,2^2}.\sqrt{0,9^2}$

$=1,2.0,9=1,08.$

c) Ta có:

$\sqrt{\dfrac{165^{2}-124^{2}}{164}}=\sqrt{\dfrac{(165-124)(165+124)}{164}}$ $\sqrt{\dfrac{165^{2}-124^{2}}{164}}=\sqrt{\dfrac{(165-124)(165+124)}{164}}$

$=\sqrt{\dfrac{41.289}{41.4}}=\sqrt{\dfrac{289}{4}}$ $=\sqrt{\dfrac{41.289}{41.4}}=\sqrt{\dfrac{289}{4}}$

$=\dfrac{\sqrt{289}}{\sqrt{4}}=\dfrac{\sqrt{17^2}}{\sqrt{2^2}}=\dfrac{17}{2}.$ $=\dfrac{\sqrt{289}}{\sqrt{4}}=\dfrac{\sqrt{17^2}}{\sqrt{2^2}}=\dfrac{17}{2}.$

Câu d: Ta có:

$\sqrt{\dfrac{149^{2}-76^{2}}{457^{2}-384^{2}}}=\sqrt{\dfrac{(149-76)(149+76)}{(457-384)(457+384)}}$ $\sqrt{\dfrac{149^{2}-76^{2}}{457^{2}-384^{2}}}=\sqrt{\dfrac{(149-76)(149+76)}{(457-384)(457+384)}}$

$=\sqrt{\dfrac{73.225}{73.841}}=\sqrt{\dfrac{225}{841}}$ $=\sqrt{\dfrac{73.225}{73.841}}=\sqrt{\dfrac{225}{841}}$

Bài 33 trang 19 sgk Toán 9 tập 1

Giải phương trình

a) $\sqrt 2 .x - \sqrt {50} = 0;$ $\sqrt 2 .x - \sqrt {50} = 0;$

b) $\sqrt 3 .x + \sqrt 3 = \sqrt {12} + \sqrt {27};$ $\sqrt 3 .x + \sqrt 3 = \sqrt {12} + \sqrt {27};$

c) $\sqrt 3 .{x^2} - \sqrt {12} = 0;$ $\sqrt 3 .{x^2} - \sqrt {12} = 0;$

d) $\dfrac{x^2}{\sqrt 5 } - \sqrt {20} = 0$ $\dfrac{x^2}{\sqrt 5 } - \sqrt {20} = 0$

Hướng dẫn giải:

a)

$\sqrt{2}.x - \sqrt{50} = 0$ $\sqrt{2}.x - \sqrt{50} = 0$

$\Leftrightarrow \sqrt{2}x=\sqrt{50}$ $\Leftrightarrow \sqrt{2}x=\sqrt{50}$

$\Leftrightarrow x=\dfrac{\sqrt{50}}{\sqrt{2}}$ $\Leftrightarrow x=\dfrac{\sqrt{50}}{\sqrt{2}}$

$\Leftrightarrow x =\sqrt{\dfrac{50}{2}}$ $\Leftrightarrow x =\sqrt{\dfrac{50}{2}}$

$\Leftrightarrow x= \sqrt{25}$ $\Leftrightarrow x= \sqrt{25}$

$\Leftrightarrow x= \sqrt{5^2}$ $\Leftrightarrow x= \sqrt{5^2}$

$\Leftrightarrow x=5.$ $\Leftrightarrow x=5.$

Vậy $x=5.$

b)

$\sqrt{3}.x + \sqrt{3} = \sqrt{12} + \sqrt{27}$ $\sqrt{3}.x + \sqrt{3} = \sqrt{12} + \sqrt{27}$

$\Leftrightarrow \sqrt{3}.x = \sqrt{12} + \sqrt{27} - \sqrt{3}$ $\Leftrightarrow \sqrt{3}.x = \sqrt{12} + \sqrt{27} - \sqrt{3}$

$\Leftrightarrow \sqrt{3}.x=\sqrt{4.3}+\sqrt{9.3}- \sqrt{3}$ $\Leftrightarrow \sqrt{3}.x=\sqrt{4.3}+\sqrt{9.3}- \sqrt{3}$

$\Leftrightarrow \sqrt{3}.x=\sqrt{4}. \sqrt{3}+\sqrt{9}. \sqrt{3}- \sqrt{3}$ $\Leftrightarrow \sqrt{3}.x=\sqrt{4}. \sqrt{3}+\sqrt{9}. \sqrt{3}- \sqrt{3}$

$\Leftrightarrow \sqrt{3}.x=\sqrt{2^2}. \sqrt{3}+\sqrt{3^3}. \sqrt{3}- \sqrt{3}$ $\Leftrightarrow \sqrt{3}.x=\sqrt{2^2}. \sqrt{3}+\sqrt{3^3}. \sqrt{3}- \sqrt{3}$

$\Leftrightarrow \sqrt{3}.x=2 \sqrt{3}+3\sqrt{3}- \sqrt{3}$ $\Leftrightarrow \sqrt{3}.x=2 \sqrt{3}+3\sqrt{3}- \sqrt{3}$

$\Leftrightarrow \sqrt{3}.x=(2+3-1).\sqrt{3}$ $\Leftrightarrow \sqrt{3}.x=(2+3-1).\sqrt{3}$

$\Leftrightarrow \sqrt{3}.x=4\sqrt{3}$ $\Leftrightarrow \sqrt{3}.x=4\sqrt{3}$

$\Leftrightarrow x=4.$ $\Leftrightarrow x=4.$

Vậy $x=4.$

c)

$\sqrt{3}x^2-\sqrt{12}=0$ $\sqrt{3}x^2-\sqrt{12}=0$

$\Leftrightarrow \sqrt{3}x^2=\sqrt{12}$ $\Leftrightarrow \sqrt{3}x^2=\sqrt{12}$

$\Leftrightarrow \sqrt{3}x^2=\sqrt{4.3}$ $\Leftrightarrow \sqrt{3}x^2=\sqrt{4.3}$

$\Leftrightarrow \sqrt{3}x^2=\sqrt{4}.\sqrt 3$ $\Leftrightarrow \sqrt{3}x^2=\sqrt{4}.\sqrt 3$

$\Leftrightarrow x^2=\sqrt{4}$ $\Leftrightarrow x^2=\sqrt{4}$

$\Leftrightarrow x^2=\sqrt{2^2}$ $\Leftrightarrow x^2=\sqrt{2^2}$

$\Leftrightarrow x^2=2$ $\Leftrightarrow x^2=2$

$\Leftrightarrow \sqrt{x^2}=\sqrt{2}$ $\Leftrightarrow \sqrt{x^2}=\sqrt{2}$

$\Leftrightarrow |x|= \sqrt 2$ $\Leftrightarrow |x|= \sqrt 2$

$\Leftrightarrow x= \pm \sqrt 2.$ $\Leftrightarrow x= \pm \sqrt 2.$

Vậy $x= \pm\sqrt 2.$ $x= \pm\sqrt 2.$

d)

$\dfrac{x^{2}}{\sqrt{5}}- \sqrt{20} = 0$ $\dfrac{x^{2}}{\sqrt{5}}- \sqrt{20} = 0$

$\Leftrightarrow \dfrac{x^2}{\sqrt{5}}=\sqrt{20}$ $\Leftrightarrow \dfrac{x^2}{\sqrt{5}}=\sqrt{20}$

$\Leftrightarrow x^2=\sqrt{20}.\sqrt{5}$ $\Leftrightarrow x^2=\sqrt{20}.\sqrt{5}$

$\Leftrightarrow x^2=\sqrt{20.5}$ $\Leftrightarrow x^2=\sqrt{20.5}$

$\Leftrightarrow x^2=\sqrt{100}$ $\Leftrightarrow x^2=\sqrt{100}$

$\Leftrightarrow x^2=\sqrt{10^2}$ $\Leftrightarrow x^2=\sqrt{10^2}$

$\Leftrightarrow x^2=10$ $\Leftrightarrow x^2=10$

$\Leftrightarrow \sqrt{x^2}=\sqrt {10}$ $\Leftrightarrow \sqrt{x^2}=\sqrt {10}$

$\Leftrightarrow |x|=\sqrt{10}$ $\Leftrightarrow |x|=\sqrt{10}$

$\Leftrightarrow x=\pm \sqrt{10}.$ $\Leftrightarrow x=\pm \sqrt{10}.$

Vậy $x= \pm \sqrt{10}.$ $x= \pm \sqrt{10}.$

Bài 34 trang 19 sgk Toán 9 tập 1

Rút gọn các biểu thức sau:

a) $ab^{2}.\sqrt{\dfrac{3}{a^{2}b^{4}}}$ $ab^{2}.\sqrt{\dfrac{3}{a^{2}b^{4}}}$ với $a < 0,\ b ≠ 0;$ $a < 0,\ b ≠ 0;$

b) $\sqrt{\dfrac{27(a - 3)^{2}}{48}}$ $\sqrt{\dfrac{27(a - 3)^{2}}{48}}$với $a > 3;$

c) $\sqrt{\dfrac{9+12a+4a^{2}}{b^{2}}}$ $\sqrt{\dfrac{9+12a+4a^{2}}{b^{2}}}$ với $a ≥ -1,5$ và $b < 0.$

d) $(a - b).\sqrt{\dfrac{ab}{(a - b)^{2}}}$ $(a - b).\sqrt{\dfrac{ab}{(a - b)^{2}}}$ với $a < b < 0.$

Hướng dẫn giải:

a) Ta có:

$(ab^{2}.\sqrt{\dfrac{3}{a^{2}b^{4}}}=ab^2.\dfrac{\sqrt{3}}{\sqrt{a^2b^4}}=ab^2.\dfrac{\sqrt{3}}{\sqrt{a^2}.\sqrt{b^4}}$ $(ab^{2}.\sqrt{\dfrac{3}{a^{2}b^{4}}}=ab^2.\dfrac{\sqrt{3}}{\sqrt{a^2b^4}}=ab^2.\dfrac{\sqrt{3}}{\sqrt{a^2}.\sqrt{b^4}}$

$=ab^2.\dfrac{\sqrt{3}}{\sqrt{a^2}.\sqrt{(b^2)^2}}=ab^2.\dfrac{\sqrt{3}}{|a|.|b^2|}$ $=ab^2.\dfrac{\sqrt{3}}{\sqrt{a^2}.\sqrt{(b^2)^2}}=ab^2.\dfrac{\sqrt{3}}{|a|.|b^2|}$

$=ab^2.\dfrac{\sqrt{3}}{-ab^2}=-\sqrt{3}.$ $=ab^2.\dfrac{\sqrt{3}}{-ab^2}=-\sqrt{3}.$

(Vì $a < 0$ nên $|a|=-a$ và $b \ne 0$ $b \ne 0$ nên $b^2 >0 \Rightarrow |b^2|=b^2) .$ $b^2 >0 \Rightarrow |b^2|=b^2) .$

b) Ta có:

$\sqrt{\dfrac{27(a - 3)^{2}}{48}}=\sqrt{\dfrac{27}{48}.(a-3)^2}=\sqrt{\dfrac{27}{48}}.\sqrt{(a-3)^2}$ $\sqrt{\dfrac{27(a - 3)^{2}}{48}}=\sqrt{\dfrac{27}{48}.(a-3)^2}=\sqrt{\dfrac{27}{48}}.\sqrt{(a-3)^2}$

$=\sqrt{\dfrac{9.3}{16.3}}.\sqrt{(a-3)^2}=\sqrt{\dfrac{9}{16}}.\sqrt{(a-3)^2}$ $=\sqrt{\dfrac{9.3}{16.3}}.\sqrt{(a-3)^2}=\sqrt{\dfrac{9}{16}}.\sqrt{(a-3)^2}$

$=\sqrt{\dfrac{3^2}{4^2}}.\sqrt{(a-3)^2}=\dfrac{\sqrt {3^2}}{\sqrt {4^2}}.\sqrt{(a-3)^2}$ $=\sqrt{\dfrac{3^2}{4^2}}.\sqrt{(a-3)^2}=\dfrac{\sqrt {3^2}}{\sqrt {4^2}}.\sqrt{(a-3)^2}$

$=\dfrac{3}{4}|a-3|=\dfrac{3}{4}(a-3).$ $=\dfrac{3}{4}|a-3|=\dfrac{3}{4}(a-3).$

( Vì $a > 3$ nên $a-3>0 \Rightarrow |a-3|=a-3)$ $a-3>0 \Rightarrow |a-3|=a-3)$

c) Ta có:

$\sqrt{\dfrac{9+12a+4a^{2}}{b^{2}}}=\sqrt{\dfrac{3^2+2.3.2a+2^2.a^2}{b^2}}$ $\sqrt{\dfrac{9+12a+4a^{2}}{b^{2}}}=\sqrt{\dfrac{3^2+2.3.2a+2^2.a^2}{b^2}}$

$=\sqrt{\dfrac{3^2+2.3.2a+(2a)^2}{b^2}}=\sqrt{\dfrac{(3+2a)^2}{b^2}}$ $=\sqrt{\dfrac{3^2+2.3.2a+(2a)^2}{b^2}}=\sqrt{\dfrac{(3+2a)^2}{b^2}}$

$=\dfrac{\sqrt{(3+2a)^2}}{\sqrt{b^2}}=\dfrac{|3+2a|}{|b|}$ $=\dfrac{\sqrt{(3+2a)^2}}{\sqrt{b^2}}=\dfrac{|3+2a|}{|b|}$

Vì $a \geq -1,5 \Rightarrow a+1,5>0$ $a \geq -1,5 \Rightarrow a+1,5>0$

$\Leftrightarrow 2(a+1,5)>0$ $\Leftrightarrow 2(a+1,5)>0$

$\Leftrightarrow 2a+3>0$ $\Leftrightarrow 2a+3>0$

$\Leftrightarrow 3+2a>0$ $\Leftrightarrow 3+2a>0$

$\Rightarrow |3+2a|=3+2a$ $\Rightarrow |3+2a|=3+2a$

Vì $b<0\Rightarrow |b|=-b$ $b<0\Rightarrow |b|=-b$

Do đó: $\dfrac{|3+2a|}{|b|}=\dfrac{3+2a}{-b} =-\dfrac{3+2a}{b}.$ $\dfrac{|3+2a|}{|b|}=\dfrac{3+2a}{-b} =-\dfrac{3+2a}{b}.$

Vậy $\sqrt{\dfrac{9+12a+4a^{2}}{b^{2}}}=-\dfrac{3+2a}{b}.$ $\sqrt{\dfrac{9+12a+4a^{2}}{b^{2}}}=-\dfrac{3+2a}{b}.$

d) Ta có:

$(a - b).\sqrt{\dfrac{ab}{(a - b)^{2}}}=(a-b).\dfrac{\sqrt{ab}}{\sqrt{(a-b)^2}}$ $(a - b).\sqrt{\dfrac{ab}{(a - b)^{2}}}=(a-b).\dfrac{\sqrt{ab}}{\sqrt{(a-b)^2}}$

$=(a-b).\dfrac{\sqrt{ab}}{|a-b|}$ $=(a-b).\dfrac{\sqrt{ab}}{|a-b|}$

$=(a-b).\dfrac{\sqrt{ab}}{-(a-b)}=-\sqrt{ab}.$ $=(a-b).\dfrac{\sqrt{ab}}{-(a-b)}=-\sqrt{ab}.$

Bài 35 trang 20 sgk Toán 9 tập 1

Tìm x, biết:

a) $\sqrt {{{\left( {x - 3} \right)}^2}} = 9;$ $\sqrt {{{\left( {x - 3} \right)}^2}} = 9;$

b) $\sqrt {4{{\rm{x}}^2} + 4{\rm{x}} + 1} = 6.$ $\sqrt {4{{\rm{x}}^2} + 4{\rm{x}} + 1} = 6.$

Hướng dẫn giải:

a) Ta có:

$\sqrt {{{\left( {x - 3} \right)}^2}} = 9 \Leftrightarrow \left| {x - 3} \right| = 9$ $\sqrt {{{\left( {x - 3} \right)}^2}} = 9 \Leftrightarrow \left| {x - 3} \right| = 9$

$\Leftrightarrow \left[ \matrix{ x - 3 = 9 \hfill \cr x - 3 = - 9 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{ x = 9 + 3 \hfill \cr x = - 9 + 3 \hfill \cr} \right.$ $\Leftrightarrow \left[ \matrix{ x - 3 = 9 \hfill \cr x - 3 = - 9 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{ x = 9 + 3 \hfill \cr x = - 9 + 3 \hfill \cr} \right.$

$\Leftrightarrow \left[ \matrix{ x = 12 \hfill \cr x = - 6 \hfill \cr} \right.$ $\Leftrightarrow \left[ \matrix{ x = 12 \hfill \cr x = - 6 \hfill \cr} \right.$

Vậy phương trình đã cho có hai nghiệm: $x = 12$ và $x = -6.$

b) Ta có:

$\sqrt{4x^2+4x+1}=6 \Leftrightarrow \sqrt{2^2x^2+4x+1}=6$ $\sqrt{4x^2+4x+1}=6 \Leftrightarrow \sqrt{2^2x^2+4x+1}=6$

$\Leftrightarrow \sqrt{(2x)^2+2.2x+1^2}=6$ $\Leftrightarrow \sqrt{(2x)^2+2.2x+1^2}=6$

$\Leftrightarrow \sqrt{(2x+1)^2}=6$ $\Leftrightarrow \sqrt{(2x+1)^2}=6$

$\Leftrightarrow |2x+1| =6$ $\Leftrightarrow |2x+1| =6$

$\eqalign{ & \Leftrightarrow \left[ \matrix{ 2x + 1 = 6 \hfill \cr 2x + 1 = - 6 \hfill \cr} \right. \cr & \Leftrightarrow \left[ \matrix{ 2x = 6 - 1 \hfill \cr 2x = - 6 - 1 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{ 2x = 5 \hfill \cr 2x = - 7 \hfill \cr} \right. \cr & \Leftrightarrow \left[ \matrix{ x = \dfrac{5}{2} \hfill \cr x = \dfrac{-7}{2} \hfill \cr} \right. \cr} .$ $\eqalign{ & \Leftrightarrow \left[ \matrix{ 2x + 1 = 6 \hfill \cr 2x + 1 = - 6 \hfill \cr} \right. \cr & \Leftrightarrow \left[ \matrix{ 2x = 6 - 1 \hfill \cr 2x = - 6 - 1 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{ 2x = 5 \hfill \cr 2x = - 7 \hfill \cr} \right. \cr & \Leftrightarrow \left[ \matrix{ x = \dfrac{5}{2} \hfill \cr x = \dfrac{-7}{2} \hfill \cr} \right. \cr} .$

Vậy phương trình có 2 nghiệm $x = \dfrac{5}{2}$ $x = \dfrac{5}{2}$ và $x=\dfrac{-7}{2}.$ $x=\dfrac{-7}{2}.$

Bài 36 trang 20 SGK Toán 9 tập 1

Mỗi khẳng định sau đúng hay sai? Vì sao?

$a) 0,01 = \sqrt {0,0001} ;$ $a) 0,01 = \sqrt {0,0001} ;$

$b) - 0,5 = \sqrt { - 0,25} ;$ $b) - 0,5 = \sqrt { - 0,25} ;$

$c) \sqrt {39} < 7$ $c) \sqrt {39} < 7$ và $\sqrt {39} > 6;$ $\sqrt {39} > 6;$

$d) \left( {4 - 13} \right).2{\rm{x}} < \sqrt 3 \left( {4 - \sqrt {13} } \right) \Leftrightarrow 2{\rm{x}} < \sqrt {3} .$ $d) \left( {4 - 13} \right).2{\rm{x}} < \sqrt 3 \left( {4 - \sqrt {13} } \right) \Leftrightarrow 2{\rm{x}} < \sqrt {3} .$

Hướng dẫn giải:

a) Đúng.

Vì $VP=\sqrt{0,0001}=\sqrt{0,01^2}=0,01=VT.$ $VP=\sqrt{0,0001}=\sqrt{0,01^2}=0,01=VT.$

b) Sai.

Vì số âm không có căn bậc hai.

c) Đúng. Vì:

$\left\{ \matrix{ {6^2} = 36 \hfill \cr {\left( {\sqrt {39} } \right)^2} = 39 \hfill \cr {7^2} = 49 \hfill \cr} \right.$ $\left\{ \matrix{ {6^2} = 36 \hfill \cr {\left( {\sqrt {39} } \right)^2} = 39 \hfill \cr {7^2} = 49 \hfill \cr} \right.$

Mà $36 < 39 < 49\Leftrightarrow \sqrt {36} < \sqrt {39} < \sqrt {49}$ $36 < 39 < 49\Leftrightarrow \sqrt {36} < \sqrt {39} < \sqrt {49}$

$\Leftrightarrow \sqrt {{6^2}} < \sqrt {39} < \sqrt {{7^2}}$ $\Leftrightarrow \sqrt {{6^2}} < \sqrt {39} < \sqrt {{7^2}}$

$\Leftrightarrow 6 < \sqrt {39} < 7$ $\Leftrightarrow 6 < \sqrt {39} < 7$

Hay $\sqrt{39}>6$ $\sqrt{39}>6$ và $\sqrt{39} < 7.$ $\sqrt{39} < 7.$

d) Đúng.

Xét bất phương trình đề cho:

$(4-\sqrt{13}).2x<\sqrt 3 .(4-\sqrt{13})(1)$ $(4-\sqrt{13}).2x<\sqrt 3 .(4-\sqrt{13})(1)$

Ta có:

$\left\{ \matrix{ {4^2} = 16 \hfill \cr {\left( {\sqrt {13} } \right)^2} = 13 \hfill \cr} \right.$ $\left\{ \matrix{ {4^2} = 16 \hfill \cr {\left( {\sqrt {13} } \right)^2} = 13 \hfill \cr} \right.$

Mà $16>13 \Leftrightarrow \sqrt{16} > \sqrt{13}$ $16>13 \Leftrightarrow \sqrt{16} > \sqrt{13}$

$\Leftrightarrow \sqrt{4^2}> \sqrt{13}$ $\Leftrightarrow \sqrt{4^2}> \sqrt{13}$

$\Leftrightarrow 4> \sqrt{13}$ $\Leftrightarrow 4> \sqrt{13}$

$\Leftrightarrow 4-\sqrt{13}>0$ $\Leftrightarrow 4-\sqrt{13}>0$

Chia cả hai vế của bất đẳng thức $(1)$ cho số dương $(4-\sqrt{13})$ $(4-\sqrt{13})$, ta được:

$\dfrac{(4-\sqrt{13}).2x}{(4-\sqrt{13})} <\dfrac{\sqrt 3 .(4-\sqrt{13})}{(4-\sqrt{13})}$ $\dfrac{(4-\sqrt{13}).2x}{(4-\sqrt{13})} <\dfrac{\sqrt 3 .(4-\sqrt{13})}{(4-\sqrt{13})}$

$\Leftrightarrow 2x < \sqrt 3.$ $\Leftrightarrow 2x < \sqrt 3.$

Vậy phép biến đổi tương đương trong câu d là đúng.

Bài 37 trang 20 SGK Toán 9 tập 1

Đố:

Trên lưới ô vuông, mỗi ô vuông cạnh

Đố: Trên lưới ô vuông, mỗi ô vuông cạnh 1cm1cm, cho bốn điểm M, N, P, QM, N, P, Q (h.3).

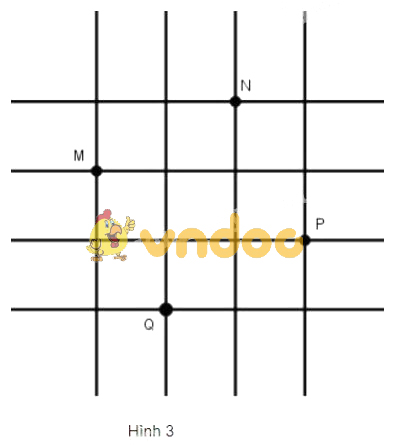
Giải bài tập SGK Toán lớp 9 bài 4: Liên hệ giữa phép chia và phép khai phương

Hãy xác định số đo cạnh, đường chéo và diện tích của tứ giác MNPQMNPQ.

Hướng dẫn giải:

Nối các điểm ta có tứ giác MNPQ

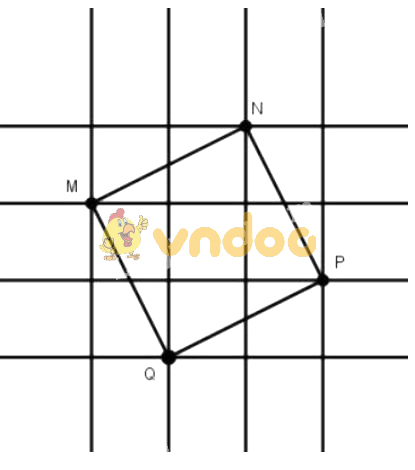
Giải bài tập SGK Toán lớp 9 bài 4: Liên hệ giữa phép chia và phép khai phương

Tứ giác MNPQ có:

- Các cạnh bằng nhau và cùng bằng đường chéo của hình chữ nhật có chiều dài 2cm, chiều rộng 1cm. Do đó theo định lí Py-ta-go:

$MN=NP=PQ=QM=\sqrt{2^{2}+1^{2}}=\sqrt{5} (cm).$ $MN=NP=PQ=QM=\sqrt{2^{2}+1^{2}}=\sqrt{5} (cm).$

- Các đường chéo bằng nhau và cùng bằng đường chéo của hình chữ nhật có chiều dài 3cm, chiều rộng 1cm nên độ dài đường chéo là:

$MP=NQ=\sqrt{3^{2}+1^{2}}=\sqrt{10}(cm).$ $MP=NQ=\sqrt{3^{2}+1^{2}}=\sqrt{10}(cm).$

Từ các kết quả trên suy ra MNPQ là hình vuông. Vậy diện tích tứ giác MNPQ bằng $MN^{2}=(\sqrt{5})^{2}=5(cm).$ $MN^{2}=(\sqrt{5})^{2}=5(cm).$

C. Trắc nghiệm Toán 9 bài 4

..........................

Ngoài tài liệu trên, mời các bạn tham khảo thêm Giải Toán 9, Tài liệu học tập lớp 9, và các đề học kì 1 lớp 9 và đề thi học kì 2 lớp 9 mới nhất được cập nhật.

Bài tiếp theo: Giải Toán 9 bài 5: Bảng Căn bậc hai

Tải về

Chọn file muốn tải về:

Giải Toán 9 bài 4 Liên hệ giữa phép chia và phép khai phương

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

30 lượt tải tài liệu

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Chia sẻ bởi:
Công Tử

22

31.619

Bài trước

Bài sau

Có thể bạn quan tâm

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!