Toán lớp 9: Lý thuyết về tính chất của hai tiếp tuyến cắt nhau

Lý thuyết về tính chất của hai tiếp tuyến cắt nhau

Toán lớp 9: Lý thuyết về tính chất của hai tiếp tuyến cắt nhau giúp các bạn học sinh ôn tập và kiểm tra trình độ kiến thức môn Toán, đồng thời rèn luyện kĩ năng vận dụng lý thuyết vào thực hành giải bài tập để hiểu bài rõ hơn, nắm chắc kiến thức hơn. Hi vọng tài liệu này sẽ giúp các bạn học tốt môn Toán lớp 9. Mời các bạn tham khảo.

Tóm tắt kiến thức:

1. Định lý

Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì:

- Điểm đó cách đều hai điểm.

- Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.

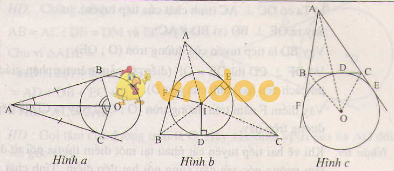
- Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm (h.a).

2. Đường tròn nội tiếp tam giác

Đường tròn nội tiếp tam giác là đường tròn tiếp xúc với ba cạnh của tam giác, còn tam giác gọi là ngoại tiếp đường tròn.

Tâm của đường tròn nội tiếp tam giác là giao điểm của các đường phân giác các góc trong của tam giác (h.b).

3. Đường tròn bàng tiếp tam giác

Đường tròn bàng tiếp tam giác là đường tròn tiếp xúc với một cạnh của tam giác và tiếp xúc với các phần kéo dài của hai cạnh kia.

Tâm của đường tròn bàng tiếp trong góc A là giao điểm của hai đường phân giác các góc ngoài tại B và C, giao điểm này cùng nằm trên đường phân giác góc A (h.c).

Với một tam giác, có ba đường tròn bàng tiếp.

Bài tập

Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm).

a) Chứng minh rằng OA vuông góc với BC.

b) Vẽ đường kính CD. Chứng minh rằng BD song song với AO.

c) Tính độ dài các cạnh của tam giác ABC; biết OB=2cm, OA=4cm.

Hướng dẫn giải:

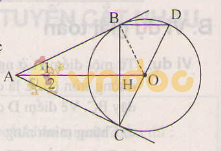
Tam giác ABC cân, có một góc 60⁰ nên là tam giác đều.

Ta có AB² = OA² - OB² = 4² - 2² = 12 ⇒ AB = 2√3

Vậy AB = AC = BC = 2√3cm

Nhận xét.

Qua câu c) ta thấy: Góc tạo bởi hai tiếp tuyến của một đường tròn vẽ từ một điểm cách tâm một khoảng bằng đường kính đúng bằng 60⁰