VnDoc.com

Giải Toán 9 Bài 2: Liên hệ giữa dây và cung

Giải SGK Toán 9 Tập 2 trang 71

Bài trước

Bài sau

Giải Toán 9 Bài 2: Liên hệ giữa dây và cung hướng dẫn các bạn học sinh trả lời các câu hỏi trong sách giáo khoa Toán lớp 9 trang 69, 70. Thông qua tài liệu này, các bạn học sinh có thể so sánh, đối chiếu với kết quả bài làm của mình, từ đó nâng cao kỹ năng giải Toán 9. Sau đây mời các bạn tham khảo chi tiết.

Lý thuyết Liên hệ giữa dây và cung

1. Định lí 1

Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:

Hai cung bằng nhau căng hai dây bằng nhau.
Hai dây bằng nhau căng hai cung bằng nhau.

2. Định lí 2

Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:

Cung lớn hơn căng dây lớn hơn.
Dây lớn hơn căng cung lớn hơn.

3. Bổ sung

Trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau.
Trong một đường tròn, đường kính đi qua điểm chính giữa của một cung thì đi qua trung điểm của dây căng cung ấy.
Trong một đường tròn, đường kính đi qua trung điểm của một dây (không đi qua tâm) thì đi qua điểm chính giữa của cung bị căng bởi dây ấy.
Trong một đường tròn, đường kính đi qua điểm chính giữa của một cung thì vuông góc với dây căng cung ấy và ngược lại.

Bài 10 trang 71 SGK Toán 9 Tập 2

a) Vẽ đường tròn tâm O, bán kính R = 2cm. Nêu cách vẽ cung AB có số đo bằng 60^o. Hỏi dây AB dài bao nhiêu xentimet?

b) Làm thế nào để chia được đường tròn thành sáu cung bằng nhau như trên hình 12?

Hướng dẫn giải:

a) Vẽ đường tròn (O; R). Vẽ góc ở tâm có số đo 60^0. Góc này là góc ở tâm chắn $\overparen{AB}$ $\overparen{AB}$ có số đo $60^0$ (hình a).

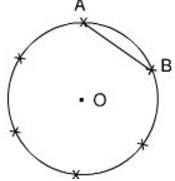
Tam giác AOB cân có $\widehat{O}=60^0$ $\widehat{O}=60^0$ nên AOB là tam giác đều, suy ra AB = R.

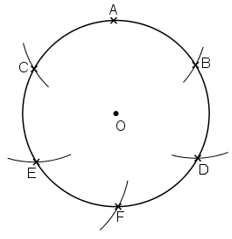
b) Theo câu a, ta có góc ở tâm bằng sđ $\overparen{AB}=60^0$ $\overparen{AB}=60^0$. Số đo góc ở tâm vẽ được theo cách này là $360^0:60^0= 6$. Suy ra được 6 cung tròn bằng nhau trên đường tròn.

Từ đó suy ra cách vẽ như sau:

Vẽ 6 dây cung bằng nhau và bằng bán kính R:

$\overparen{{A_1}{A_2}} = \overparen{{A_2}{A_3}} = \overparen{{A_3}{A_4}}= \overparen{{A_4}{A_5}} = \overparen{{A_5}{A_6}} = \overparen{{A_6}{A_1}} = {\rm{ }}R$ $\overparen{{A_1}{A_2}} = \overparen{{A_2}{A_3}} = \overparen{{A_3}{A_4}}= \overparen{{A_4}{A_5}} = \overparen{{A_5}{A_6}} = \overparen{{A_6}{A_1}} = {\rm{ }}R$

Từ đó suy ra 6 cung bằng nhau. (hình b)

Hoặc ta có cách vẽ cụ thể như sau:

Chia đường tròn thành 6 cung bằng nhau:

+ Vẽ đường tròn tâm O, bán kính R.

+ Trên đường tròn tâm O, lấy điểm A ₁

+ Vẽ cung tròn tâm A ₁, bán kính R cắt đường tròn tại A₂ và A₆

+ Vẽ cung tròn tâm A₂ và A₆ bán kính R cắt đường tròn tâm O tại giao điểm thứ hai là A₃ và A₅

+ Vẽ cung tròn tâm A₅ bán kính R cắt đường tròn (O) tại giao điểm thứ hai là $A_4.$

Khi đó, ta chia được đường tròn thành sáu cung bằng nhau như trên

Bài 11 trang 72 SGK Toán 9 Tập 2

Cho hai đường tròn bằng nhau (O) và (O') cắt nhau tại hai điểm A và B. Kẻ các đường kính AOC, AO'D. Gọi E là giao điểm thứ hai của AC với đường tròn (O').

a) So sánh các cung nhỏ BC, BD.

b) Chứng mình rằng B là điểm chính giữa của cung EBD (tức là điểm B chia cung EBD thành hai cung bằng nhau:

Hướng dẫn giải:

Vẽ hình minh họa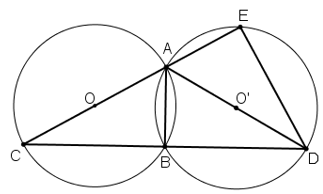

a) Vì $\left( O \right)$ $\left( O \right)$ và $\left( {O$ $\left( {O'} \right)$ cắt nhau tại hai điểm A và B nên $OO' \bot AB$ (định lý)

Xét tam giác ADC có OO' là đường trung bình (vì O là trung điểm AC,O' là trung điểm AD) nên OO'//CD , suy ra $AB \bot CD$ $AB \bot CD$ (quan hệ từ vuông góc đến song song).

Xét tam giác ADC có AC = AD (vì hai đường tròn $\left( O \right)$ $\left( O \right)$ và $\left( {O$ $\left( {O'} \right)$ có cùng bán kính) nên $\Delta ACD$ $\Delta ACD$ cân tại A có AB là đường cao nên AB cũng là đường trung tuyến, suy ra BC = BD hay cung BC = cung BD (vì (O) và (O') là hai đường tròn bằng nhau).

b) Xét đường tròn (O') có A,E,D cùng thuộc đường tròn và AD là đường kính nên tam giác AED vuông tại E $\Rightarrow DE \bot AC \Rightarrow \widehat {DEC} = 90^\circ .$ $\Rightarrow DE \bot AC \Rightarrow \widehat {DEC} = 90^\circ .$

Xét tam giác DEC vuông tại E có B là trung điểm $DC\left( {cmt} \right) \Rightarrow EB = \dfrac{{DC}}{2} = BD = EB$ $DC\left( {cmt} \right) \Rightarrow EB = \dfrac{{DC}}{2} = BD = EB$

Suy ra cung EB=cung BD (định lý), do đó B là điểm chính giữa cung ED..

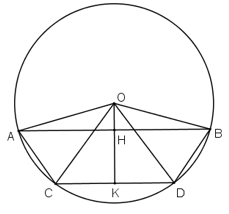
Bài 12 trang 72 SGK Toán 9 Tập 2

Cho tam giác ABC . Trên tia đối của tia AB lấy một điểm D sao cho AD = AC. Vẽ đường tròn tâm O ngoại tiếp tam giác DBC. Từ O lần lượt hạ các đường vuông góc OH, OK với BC và BD (H ∈ BC, K ∈ BD)

a) Chứng minh rằng OH > OK.

b) So sánh hai cung nhỏ BD và BC.

Hướng dẫn giải:

Vẽ hình

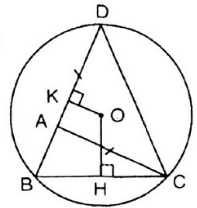
a) Xét ΔABC có: BC < AB + AC (Bất đẳng thức tam giác)

Mà AD = AC (gt)

⇒ BC < AB + AD = BD

Mà OH là khoảng cách từ O đến dây BC

OK là khoảng cách từ O đến dây BD

⇒ OH > OK.( định lý về khoảng cách từ tâm đến dây)

b) Vì BD > BC

nên suy ra $\overparen{BC}$ $\overparen{BC}$ nhỏ hơn $\overparen{BD}$ $\overparen{BD}$ ( liên hệ cung và dây)

Bài 13 trang 72 SGK Toán 9 Tập 2

Chứng minh rằng: trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau.

Hướng dẫn giải:

TH1: Tâm đường tròn nằm trong hai dây song song

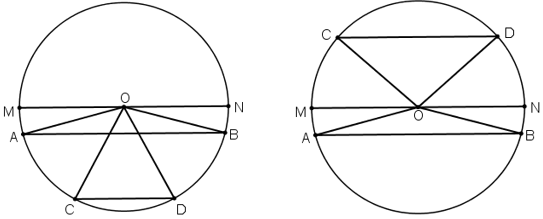
Giả sử AB và CD là các dây song song của đường tròn (O). Ta chứng minh $\overparen{AC}= \overparen{BD}.$ $\overparen{AC}= \overparen{BD}.$

Kẻ $OI \bot AB (I \in AB)$ $OI \bot AB (I \in AB)$ và $OK \bot CD (K\in CD)$ $OK \bot CD (K\in CD)$.

Do AB //CD nên I,O,K thẳng hàng.

Do các tam giác OAB, OCD là các tam giác cân đỉnh O nên các đường cao kẻ từ đỉnh đồng thời là phân giác.

Vì vậy ta có: $\widehat {{O_1}} = \widehat {{O_2}}$ $\widehat {{O_1}} = \widehat {{O_2}}$ và $\widehat {{O_3}} = \widehat {{O_4}}$ $\widehat {{O_3}} = \widehat {{O_4}}$

Ta có: $\widehat {AOC} = {180^0} - \widehat {{O_1}} - \widehat {{O_3}} = {180^0} - \widehat {{O_2}} - \widehat {{O_4}} = \widehat {BOD}$ $\widehat {AOC} = {180^0} - \widehat {{O_1}} - \widehat {{O_3}} = {180^0} - \widehat {{O_2}} - \widehat {{O_4}} = \widehat {BOD}$

Suy ra $\overparen{AC}= \overparen{BD}.$ $\overparen{AC}= \overparen{BD}.$

TH2: Tâm đường tròn nằm ngoài hai dây song song

Giả sử đường tròn $\left( O \right)$ $\left( O \right)$ có hai dây song song AB//CD. Ta chứng minh cung AC = cung BD .

Qua O kẻ đường kính EG//CD ⇒ EG//AB .

Nối OA,OC,OB,OD ⇒ OA = OB = OC = OD (= bán kính)

+ Xét tam giác OAB cân tại $O\left( {{\rm{do}}\,OA = OB} \right)$ $O\left( {{\rm{do}}\,OA = OB} \right)$ nên $\widehat {OAB} = \widehat {OBA}$ $\widehat {OAB} = \widehat {OBA}$(1)

Lại có $EG//AB \Rightarrow \widehat {OAB} = \widehat {AOE};\,\widehat {OBA} = \widehat {BOG}$ $EG//AB \Rightarrow \widehat {OAB} = \widehat {AOE};\,\widehat {OBA} = \widehat {BOG}$ (so le trong) (2)

Từ (1) và (2) suy ra $\widehat {EOA} = \widehat {BOG}$ $\widehat {EOA} = \widehat {BOG}$(*)

+ Xét tam giác OCD cân tại $O\left( {{\rm{do}}\,OC = OD} \right)$ $O\left( {{\rm{do}}\,OC = OD} \right)$ nên $\widehat {OCD} = \widehat {ODC} (3)$ $\widehat {OCD} = \widehat {ODC} (3)$

Lại có $EG//CD \Rightarrow \widehat {OCD} = \widehat {COE};\,\widehat {ODC} = \widehat {DOG}$ $EG//CD \Rightarrow \widehat {OCD} = \widehat {COE};\,\widehat {ODC} = \widehat {DOG}$ (so le trong) (4)

Từ (3) và (4) suy ra $\widehat {EOC} = \widehat {DOG}$ $\widehat {EOC} = \widehat {DOG}$(**)

Từ (*) và (**) suy ra $\widehat {EOA} - \widehat {EOC} = \widehat {BOG} - \widehat {DOG} \Leftrightarrow \widehat {AOC} = \widehat {BOD} \Rightarrow \overparen{AC}=\overparen{BD}$ $\widehat {EOA} - \widehat {EOC} = \widehat {BOG} - \widehat {DOG} \Leftrightarrow \widehat {AOC} = \widehat {BOD} \Rightarrow \overparen{AC}=\overparen{BD}$(đpcm)

Bài 14 trang 72 SGK Toán 9 Tập 2

a) Chứng minh rằng đường kính đi qua điểm chính giữa của một cung thì đi qua trung điểm của dây cung căng cung ấy. Mệnh đề đảo có đúng không? Hãy nêu thêm điều kiện để mệnh đề đảo đúng.

b) Chứng minh rằng đường kính đi qua điểm chính giữa của một cung thì vuông góc với dây cung ấy và ngược lại.

Hướng dẫn giải:

Vẽ hình minh họa

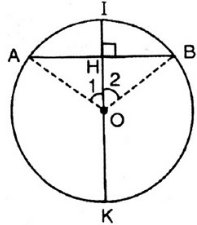
Giả sử đường tròn (O) có đường IK và I là điểm chính giữa cung AB.

a) Vì I là điểm chính giữa của \overparen{AB}, suy ra \overparen{IA} = \overparen{IB} ⇒ IA = IB

Ta có: OA = OB = bán kính. Suy ra đường kính IK là đường trung trực của dây AB. Vậy HA = HB (đpcm)

Mệnh đề đảo: Đường kính đi qua trung điểm của một dây thì đi qua điểm chính giữa của cung căng dây đó.

Chứng minh: Vì ∆ AOB cân tại O và HA = HB nên OH là đường phân giác của góc $\widehat{AOB}$ $\widehat{AOB}$. Suy ra $\widehat {{O_1}} = \widehat {{O_2}}$ $\widehat {{O_1}} = \widehat {{O_2}}$

Từ đó suy ra $\overparen{IA} = \overparen{IB}$ $\overparen{IA} = \overparen{IB}$

Tuy nhiên khi AB đi qua tâm thì điều này chưa chắc đúng vì nếu AB tạo với IK góc $\widehat {AOI} = 30^\circ \Rightarrow \widehat {BOI} = 150^\circ \Rightarrow \overparen{IA}<\overparen{IB}$ $\widehat {AOI} = 30^\circ \Rightarrow \widehat {BOI} = 150^\circ \Rightarrow \overparen{IA}<\overparen{IB}$

Vậy phải thêm điều kiện để mệnh đề đảo đúng là:

Đường kính đi qua trung điểm của một dây không đi qua tâm thì đi qua điểm chính giữa của cung căng dây đó.

b) Hình vẽ

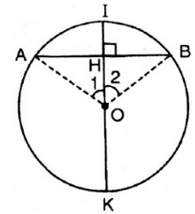
Vì I là điểm chính giữa của $\overparen{AB}$ $\overparen{AB}$, suy ra $\overparen{IA} = \overparen{IB}$ $\overparen{IA} = \overparen{IB}$ ⇒ IA = IB

Ta có: OA = OB = bán kính. Suy ra đường kính IK là đường trung trực của dây AB

Nên OI hay IK là đường trung trực của dây AB. Suy ra IK \bot AB.

* Điều ngược lại: Đường kính vuông góc ở dây khi qua tâm thì đi qua hai điểm chính giữa của cung căng dây đó.

Kẻ đường kính KOI vuông góc với AB.

Ta có OA = OB ⇒ ∆OAB cân tại O

Mà $OH \bot AB$ $OH \bot AB$ nên OH là đường phân giác của $\widehat{AOB}$ $\widehat{AOB}$ suy ra $\widehat {{O_1}} = \widehat {{O_2}}$ $\widehat {{O_1}} = \widehat {{O_2}}$

Ta có ∆OAI = ∆OBI (c.g.c). Do đó AI = IB. Suy ra $\overparen{AI} = \overparen{IB}.$ $\overparen{AI} = \overparen{IB}.$

Vậy I là điểm chính giữa của $\overparen{AB}$ $\overparen{AB}$

..................................................

Như vậy VnDoc đã giới thiệu các bạn tài liệu Giải Toán 9 Bài 2: Liên hệ giữa dây và cung. Để tham khảo lời giải những bài tiếp theo, mời các em vào chuyên mục Giải Toán 9 trên VnDoc nhé. Chuyên mục tổng hợp lời giải theo từng đơn vị bài học giúp các em nắm vững kiến thức được học trong SGK Toán 9. Chúc các em học tốt.

Bài tiếp theo: Giải Toán 9 bài 3: Góc nội tiếp.