Giải Toán 9 trang 69 tập 1 Kết nối tri thức

Giải Toán 9 trang 69 Tập 1

Hoạt động 2 Trang 69 Toán 9 Tập 1
Hoạt động 3 Trang 69 Toán 9 Tập 1

Giải Toán 9 trang 69 tập 1 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Kết nối tri thức tập 1 trang 69.

Hoạt động 2 Trang 69 Toán 9 Tập 1

Cho tam giác ABC vuông cân tại A và AB = AC = a (H.4.7a).

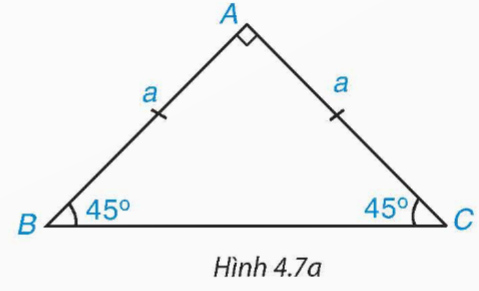
a) Hãy tính BC và các tỉ số $\frac{{AB}}{{BC}} , \ \frac{{AC}}{{BC}}$ $\frac{{AB}}{{BC}} , \ \frac{{AC}}{{BC}}$. Từ đó suy ra $\sin {45^\circ },\cos {45^\circ }.$ $\sin {45^\circ },\cos {45^\circ }.$

b) Hãy tính các tỉ số $\frac{{AB}}{{AC}}$ $\frac{{AB}}{{AC}}$ và $\frac{{AC}}{{AB}}.$ $\frac{{AC}}{{AB}}.$ Từ đó suy ra $\tan {45^\circ },\ \cot {45^\circ }.$ $\tan {45^\circ },\ \cot {45^\circ }.$

Hướng dẫn giải:

Xét tam giác ABC vuông tại A, theo định lí Pythagore, ta có:

BC² = AB² + AC² = a² + a² = 2a² nên BC = $a\sqrt{2}$ $a\sqrt{2}$ (cm)

Do đó: $\frac{AB}{BC}=\frac{AC}{BC}=\frac{a}{a\sqrt{2}}=\frac{1}{\sqrt{2}}$ $\frac{AB}{BC}=\frac{AC}{BC}=\frac{a}{a\sqrt{2}}=\frac{1}{\sqrt{2}}$

Từ đó suy ra $\sin45^o=\cos45^o=\frac{1}{\sqrt{2}}$ $\sin45^o=\cos45^o=\frac{1}{\sqrt{2}}$

b) Ta có: $\frac{{AB}}{{AC}} =\frac{{AC}}{{AB}} = \frac{a}{a} = 1$ $\frac{{AB}}{{AC}} =\frac{{AC}}{{AB}} = \frac{a}{a} = 1$

Do đó $\tan {45^\circ } =\tan {B } = \tan C = \frac{{AB}}{{AC}} = 1$ $\tan {45^\circ } =\tan {B } = \tan C = \frac{{AB}}{{AC}} = 1$

Hoạt động 3 Trang 69 Toán 9 Tập 1

Xét tam giác đều ABC có cạnh bằng 2a.

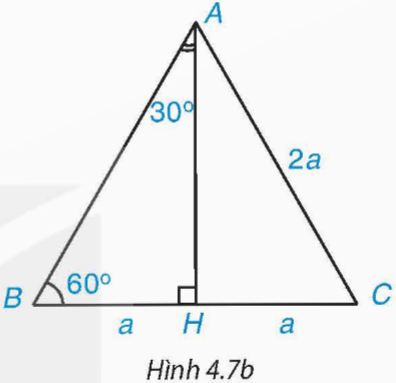
a) Tính đường cao AH của tam giác ABC (H.4.7b) .

b) Tính sin 30^o, cos 30^o, sin 60^o và cos 60^o.

c) Tính tan 30^o, cot 30^o, tan 60^o và cot 60^o.

Hướng dẫn giải:

a) Xét tam giác ABH vuông tại H, theo định lý Pythagore ta có:

AB² = AH² + HB²

Suy ra AH² = AB² − HB² = 4a² - a² = 3a²

Vậy AH = $a\sqrt{3}$ $a\sqrt{3}$

b) Xét tam giác ABH vuông tại H:

Theo định nghĩa của tỉ số lượng giác sin, côsin, ta có:

$\sin {30^0} = \sin \widehat {BAH} = \frac{{BH}}{{AB}} = \frac{a}{{2a}} = \frac{1}{2}$ $\sin {30^0} = \sin \widehat {BAH} = \frac{{BH}}{{AB}} = \frac{a}{{2a}} = \frac{1}{2}$

$\cos {30^0} = \cos \widehat {BAH} = \frac{{AH}}{{AB}} = \frac{{a\sqrt 3 }}{{2a}} = \frac{{\sqrt 3 }}{2}$ $\cos {30^0} = \cos \widehat {BAH} = \frac{{AH}}{{AB}} = \frac{{a\sqrt 3 }}{{2a}} = \frac{{\sqrt 3 }}{2}$

$\sin {60^0} = \sin \widehat {ABH} = \frac{{AH}}{{AB}} = \frac{{a\sqrt 3 }}{{2a}} = \frac{{\sqrt 3 }}{2}$ $\sin {60^0} = \sin \widehat {ABH} = \frac{{AH}}{{AB}} = \frac{{a\sqrt 3 }}{{2a}} = \frac{{\sqrt 3 }}{2}$

$\cos {60^0} = \cos \widehat {ABH} = \frac{{BH}}{{AB}} = \frac{a}{{2a}} = \frac{1}{2}$ $\cos {60^0} = \cos \widehat {ABH} = \frac{{BH}}{{AB}} = \frac{a}{{2a}} = \frac{1}{2}$

c) Xét tam giác ABH vuông tại H:

Theo định nghĩa của tỉ số lượng giác tan, côtan, ta có:

$\tan {30^0} = \tan \widehat {BAH} = \frac{{BH}}{{AH}} = \frac{a}{{a\sqrt 3 }} = \frac{{\sqrt 3 }}{3}$ $\tan {30^0} = \tan \widehat {BAH} = \frac{{BH}}{{AH}} = \frac{a}{{a\sqrt 3 }} = \frac{{\sqrt 3 }}{3}$

$\cot {30^0} = \cot \widehat {BAH} = \frac{{AH}}{{BH}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3$ $\cot {30^0} = \cot \widehat {BAH} = \frac{{AH}}{{BH}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3$

$\tan {60^0} = \tan \widehat {ABH} = \frac{{AH}}{{BH}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3$ $\tan {60^0} = \tan \widehat {ABH} = \frac{{AH}}{{BH}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3$

$\cot {60^0} = \tan \widehat {ABH} = \frac{{BH}}{{AH}} = \frac{a}{{a\sqrt 3 }} = \frac{{\sqrt 3 }}{3}$ $\cot {60^0} = \tan \widehat {ABH} = \frac{{BH}}{{AH}} = \frac{a}{{a\sqrt 3 }} = \frac{{\sqrt 3 }}{3}$

-----------------------------------------------

---> Xem thêm: Giải Toán 9 trang 70 tập 1 Kết nối tri thức

Toán 9 Kết nối tri thức Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng

Lời giải Toán 9 trang 69 Tập 1 Kết nối tri thức với các câu hỏi nằm trong Bài 11: Tỉ số lượng giác của góc nhọn, được VnDoc biên soạn và đăng tải!

Chia sẻ, đánh giá bài viết

1

51

Bài trước

Bài sau