Giải Toán 9 trang 98 tập 1 Kết nối tri thức
Giải Toán 9 trang 98 Tập 1
Giải Toán 9 trang 98 tập 1 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Kết nối tri thức tập 1 trang 98.
Bài 5.17 Trang 98 Toán 9 Tập 1
Cho đường tròn (O; 5 cm).
a) Hãy nêu cách vẽ dây AB sao cho khoảng cách từ điểm O đến dây AB bằng 2,5 cm.
b) Tính độ dài của dây AB trong câu a (làm tròn đến hàng phần trăm).
c) Tính số đo và độ dài của cung nhỏ AB.
d) Tính diện tích hình quạt tròn ứng với cung nhỏ AB.
Hướng dẫn giải:
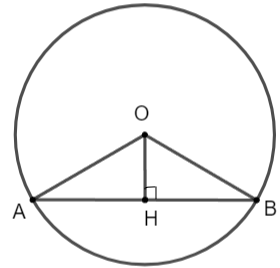
a) Lấy điểm H tùy ý sao cho OH = 2,5 cm
Vẽ đường thẳng vuông góc với OH tại H, cắt đường tròn (O) tại A và B.
Khi đó ta được dây AB
b) Xét tam giác OAH vuông tại H, ta có:
OA2 = OH2 + AH2 (định lí Pythagore)
Suy ra AH2 = OA2 - OH2
= 52 - 2,52 = 18,75 hay AH ≈ 4,33 cm
Vậy AB = 2AH ≈ 2 . 4,33 ≈ 8,66 cm.
c) Tam giác OAB cân tại O có OH là đường cao
nên OH cũng là đường phân giác của góc AOB
Xét tam giác AOH vuông tại H, ta có:
\(\cos \widehat{AOH}=\frac{OH}{OA}=\frac{1}{2} \Rightarrow \widehat{AOH}=60^{\circ}\)
Vậy sđ \(\overset \frown {AB}=\widehat{AOB}= 2\widehat{AOH}=2.60^{\circ} =120^{\circ}\)
Độ dài cung nhỏ AB là: \(\frac{120}{180}.\pi.5=\frac{10}{3}\pi\) (cm)
d) Diện tích hình quạt ứng với cung nhỏ AB là:
\(S_q=\frac{l.R}{2}=\frac{\frac{10}{3}\pi.5}{2}=\frac{25}{3}\pi\) (cm2)
Bài 5.18 Trang 98 Toán 9 Tập 1
Ba bộ phận truyền chuyển động của một chiếc xe đạp gồm một giò đĩa (bánh răng gắn với bàn đạp), một chiếc líp (cũng có dạng bánh răng) gắn với bánh xe và bộ xích (H.5.23). Biết rằng giò đĩa có bán kính 15 cm, líp có bán kính 4 cm và bánh xe có đường kính 65 cm. Hỏi khi người đi xe đạp một vòng thì xe chạy được quãng đường dài bao nhiêu mét (làm tròn kết quả đến hàng phần chục)?
Hướng dẫn giải:
Chu vi của giò đĩa là: 2πR = 2π . 15 = 30π (cm)
Chu vi của chiếc líp là: 2πR = 2π . 4 = 8π (cm)
Chu vi của bánh xe là: πd = π . 65 = 65π (cm)
Khi người đi xe đạp một vòng thì xe chạy được quãng đường là:
\(\frac{30\pi}{8\pi}.65\pi\approx765,76\) cm ≈ 7,7 m
Bài 5.19 Trang 98 Toán 9 Tập 1
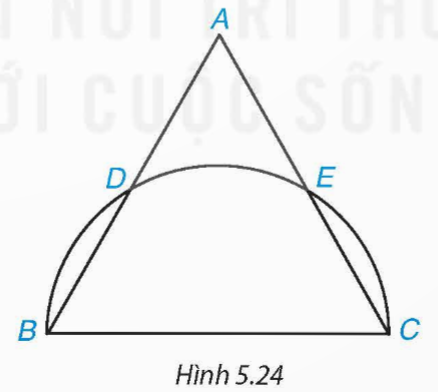
Cho tam giác đều ABC có \(AB=2\sqrt{3}\) cm. Nửa đường tròn đường kính BC cắt hai cạnh AB và AC lần lượt tại D và E (khác B và C) (H.5.24).
a) Chứng tỏ rằng ba cung nhỏ BD, DE và EC bằng nhau. Tính số đo mỗi cung ấy.
b) Tính diện tích của hình viên phân (xem ví dụ 2) giới hạn bởi dây BD và cung nhỏ BD.
Hướng dẫn giải:
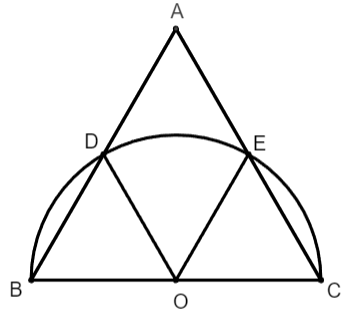
a) Gọi O là trung điểm của BC
Ta có OB = OD = R nên tam giác BOD cân tại O
Mà \(\widehat {OBD}=60^{\circ}\) nên tam giác BOD đều
Suy ra \(\widehat {BOD}=60^{\circ}\)
Tương tự ta có tam giác EOC đều nên \(\widehat {EOC}=60^{\circ}\)
Ta có \(\widehat {BOD} + \widehat {DOE} + \widehat {EOC} = {180^o}\)
\(\Rightarrow \widehat {DOE}= {180^{\circ} }- \widehat {BOD}- \widehat {EOC}\)
= 180o - 60o - 60o = 60o
Vậy \(\widehat {BOD} = \widehat {DOE} = \widehat {EOC}\) hay \(\overset\frown{BD}=\overset\frown{DE}=\overset\frown{EC}=60^{\circ}\)
b) Diện tích hình quạt tròn ứng với cung BD là:
\(S_q=\frac{60}{360}.\pi.\left(\sqrt{3}\right)^2=\frac{\pi}{2}\) (cm2)
Diện tích tam giác OBD là:
\(S_t=\frac{1}{2}.\left(\sqrt{3}\right)^2.\sin60=\frac{3\sqrt{3}}{4}\) (cm2)
Diện tích hình viên phân là:
\(S=S_q-S_t=\frac{\pi}{2}-\frac{3\sqrt{3}}{4}=\frac{1}{4}\left(2\pi-3\sqrt{3}\right)\) (cm2)
-----------------------------------------------
---> Xem thêm: Giải Toán 9 trang 99 tập 1 Kết nối tri thức
Lời giải Toán 9 trang 98 Tập 1 Kết nối tri thức với các câu hỏi nằm trong Luyện tập chung trang 96, được VnDoc biên soạn và đăng tải!
