Giải Toán 9 trang 10 tập 1 Kết nối tri thức
Giải Toán 9 trang 10 Tập 1
Giải Toán 9 trang 10 Tập 1 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Kết nối tri thức tập 1 trang 10.
Bài 1.1 trang 10 SGK Toán 9 tập 1 KNTT
Phương trình nào sau đây là phương trình bậc nhất hai ẩn? Vì sao?
a) 5x – 8y = 0;
b) 4x + 0y = –2;
c) 0x + 0y = 1;
d) 0x – 3y = 9.
Hướng dẫn giải:
a) Phương trình 5x – 8y = 0 là phương trình bậc nhất hai ẩn vì có dạng ax + by = c với hệ số a = 5 ≠ 0 và b = – 8 ≠ 0.
b) Phương trình 4x + 0y = –2 là phương trình bậc nhất hai ẩn vì có dạng ax + by = c với hệ số a = 4 ≠ 0 và b = 0.
c) Phương trình 0x + 0y = 1 không là phương trình bậc nhất hai ẩn vì có các hệ số a = 0, b = 0.
d) Phương trình 0x – 3y = 9 là phương trình bậc nhất hai ẩn vì có dạng ax + by = c với hệ số a = 0 và b = - 3 ≠ 0.
Bài 1.2 trang 10 SGK Toán 9 tập 1 KNTT
a) Tìm giá trị thích hợp thay cho dấu "?" trong bảng sau rồi cho biết 6 nghiệm của phương trình 2x – y = 1:
x | –1 | –0,5 | 0 | 0,5 | 1 | 2 |
y = 2x – 1 | ? | ? | ? | ? | ? | ? |
b) Viết nghiệm tổng quát của phương trình đã cho.
Hướng dẫn giải:
a) Ta có bảng sau:
x | - 1 | - 0,5 | 0 | 0,5 | 1 | 2 |
y = 2x - 1 | - 3 | - 2 | - 1 | 0 | 1 | 3 |
Ta có 6 nghiệm của phương trình đã cho là: (- 1; - 3), (- 0,5; - 2), (0; - 1), (0,5; 0), (1; 1), (2; 3)
b) Nghiệm tổng quát của phương trình đã cho là:
(x; 2x - 1) với x ∈ R tùy ý.
Bài 1.3 trang 10 SGK Toán 9 tập 1 KNTT
Viết nghiệm và biểu diễn hình học tất cả các nghiệm của mỗi phương trình bậc nhất hai ẩn sau:
a) 2x – y = 3;
b) 0x + 2y = –4;
c) 3x + 0y = 5.
Hướng dẫn giải:
a) 2x – y = 3 (1)
Ta viết (1) dưới dạng y = 2x - 3. Mỗi cặp số (x; 2x - 3) với x ∈ R tùy ý, là một nghiệm của (1).
Khi đó ta nói phương trình (1) có nghiệm (tổng quát) là:
(x; 2x - 3) với x ∈ R tùy ý.
Mỗi nghiệm này là tọa độ của một điểm thuộc đường thẳng y = 2x - 3. Ta cũng gọi đường thẳng này là đường thẳng d: 2x - y = 3.
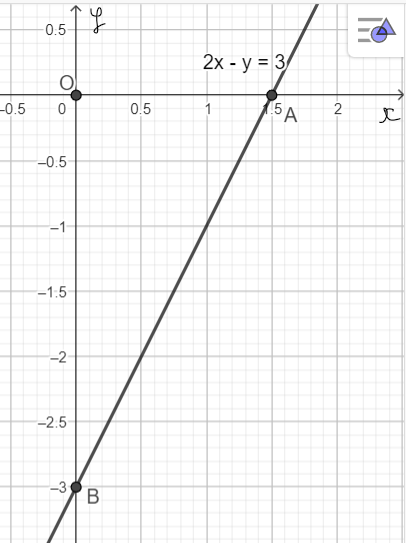
Ta xác định hai điểm tùy ý của d là A(1,5; 0) và B(0; - 3).
Ta biểu diễn hình học tất cả các nghiệm của phương trình bậc nhất hai ẩn 2x - y = 3 như sau:
b) 0x + 2y = - 4 (2)
Ta viết gọn (2) thành y = - 2. Phương trình (2) có nghiệm là (x; - 2) với x ∈ R tùy ý.
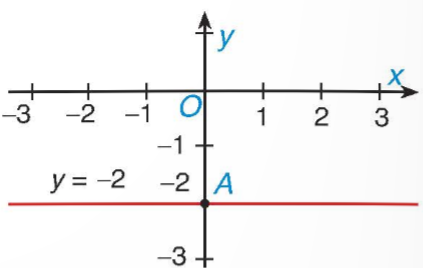
Mỗi nghiệm này là tọa độ của một điểm thuộc đường thẳng song song với trục hoành và cắt trục tung tại điểm C(0; - 2). Ta gọi đó là đường thẳng y = - 2.
Ta biểu diễn hình học tất cả các nghiệm của phương trình bậc nhất hai ẩn 0x + 2y = - 4 như sau:
c) 3x + 0y = 5 (3)
Ta viết gọn (3) thành 
. Phương trình (3) có nghiệm là (; y) với y ∈ R tùy ý.
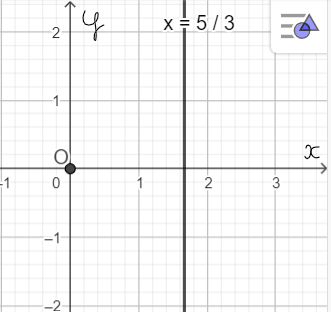
Mỗi nghiệm này là tọa độ của một điểm thuộc đường thẳng song song với trục tung và cắt trục hoành tại điểm D(; 0). Ta gọi đó là đường thẳng .
Ta biểu diễn hình học tất cả các nghiệm của phương trình bậc nhất hai ẩn 3x + 0y = 5 như sau:
Bài 1.4 trang 10 SGK Toán 9 tập 1 KNTT
Cho hệ phương trình
a) Hệ phương trình trên có là một hệ hai phương trình bậc nhất hai ẩn không? Vì sao?
b) Cặp số (–3; 4) có là một nghiệm của hệ phương trình đã cho hay không? Vì sao?
Hướng dẫn giải:
a) Hệ phương trình đã cho là hệ hai phương trình bậc nhất hai ẩn vì có hai phương trình đều là phương trình bậc nhất hai ẩn.
b) Ta thấy khi x = - 3 và y = 4 thì:
2x = 2 . (- 3) = - 6 nên (- 3; 4) là nghiệm của phương trình thứ nhất.
5x + 4y = 5 . (- 3) + 4 . 4 = 1 nên (- 3; 4) là nghiệm của phương trình thứ hai.
Vậy (- 3; 4) là nghiệm chung của hai phương trình, nghĩa là (- 3; 4) là một nghiệm của hệ phương trình đã cho.
Bài 1.5 trang 10 SGK Toán 9 tập 1 KNTT
Cho các cặp số (–2; 1), (0; 2), (1; 0), (1,5; 3), (4; –3) và hai phương trình
5x + 4y = 8, (1)
3x + 5y = –3. (2)
Trong các cặp số đã cho:
a) Những cặp số nào là nghiệm của phương trình (1)?
b) Cặp số nào là nghiệm của hệ hai phương trình gồm phương trình (1) và phương trình (2)?
c) Vẽ hai đường thẳng 5x + 4y = 8 và 3x + 5y = –3 trên cùng một mặt phẳng tọa độ để minh họa kết luận ở câu b.
Hướng dẫn giải:
a) Với phương trình (1): 5x + 4y = 8
- Thay x = - 2; y = 1, ta có:
5x + 4y = 5 . (- 2) + 4 . 1 = - 6 ≠ 8 nên (- 2; 1) không là nghiệm của phương trình (1).
- Thay x = 0; y = 2, ta có:
5x + 4y = 5 . 0 + 4 . 2 = 8 nên (0; 2) là nghiệm của phương trình (1).
- Thay x = 1; y = 0, ta có:
5x + 4y = 5 . 1 + 4 . 0 = 5 ≠ 8 nên (1; 0) không là nghiệm của phương trình (1).
- Thay x = 1,5; y = 3, ta có:
5x + 4y = 5 . 1,5 + 4 . 3 = 19,5 ≠ 8 nên (1,5; 3) không là nghiệm của phương trình (1).
- Thay x = 4; y = - 3, ta có:
5x + 4y = 5 . 4 + 4 . (- 3) = 8 nên (4; - 3) là nghiệm của phương trình (1).
Vậy cặp số là nghiệm của phương trình (1) là (0; 2) và (4; - 3).
b) Để các cặp số là nghiệm của hệ hai phương trình gồm phương trình (1) và phương trình (2) thì các cặp số đó phải là nghiệm chung của hai phương trình.
- Thay x = 0; y = 2 vào phương trình (2), ta có:
3x + 5y = 3 . 0 + 5 . 2 = 10 ≠ - 3 nên (0; 2) không là nghiệm của phương trình (2).
- Thay x = 4; y = - 3 vào phương trình (2), ta có:
3x + 5y = 3 . 4 + 5 . (- 3) = - 3 nên (4; - 3) là nghiệm của phương trình (2).
Vậy cặp số (4; - 3) là nghiệm chung của hai phương trình, nghĩa là (4; - 3) là nghiệm của hệ gồm phương trình (1) và phương trình (2).
c) Đường thẳng 5x + 4y = 8 đi qua hai điểm tùy ý là A(0; 2) và B(4; - 3).
Đường thẳng 3x + 5y = - 3 đi qua hai điểm tùy ý là B(4; - 3) và C(- 1; 0).
Ta có hình vẽ sau:
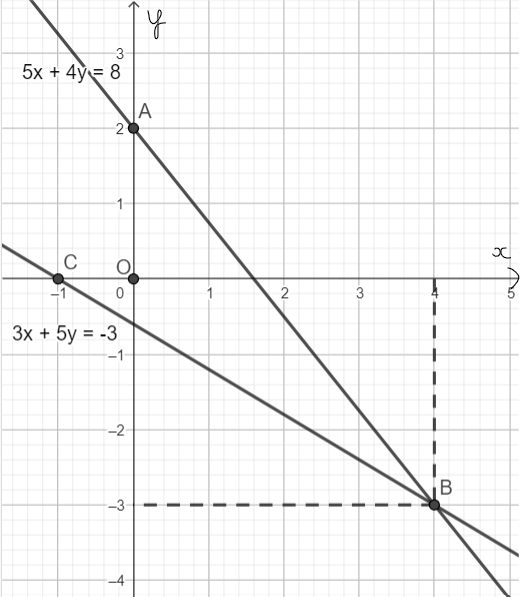
Vậy B(4; - 3) là giao điểm của hai đường thẳng 5x + 4y = 8 và 3x + 5y = –3.
-----------------------------------------------
---> Bài tiếp theo: Toán 9 Kết nối tri thức Bài 2 Giải hệ hai phương trình bậc nhất hai ẩn
Lời giải Toán 9 trang 10 Tập 1 Kết nối tri thức với các câu hỏi nằm trong Bài 1 Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn, được VnDoc biên soạn và đăng tải!
