Giải Toán 9 trang 9 tập 2 Kết nối tri thức
Giải Toán 9 trang 9 Tập 2
Bước sang học kì II lớp 9, chương trình Toán 9 Kết nối tri thức tập 2 mở ra nhiều nội dung quan trọng, có tính nền tảng cho các chuyên đề nâng cao và các dạng bài thường gặp trong kỳ thi tuyển sinh vào lớp 10. Ngay từ những bài đầu tiên, học sinh cần nắm chắc kiến thức, hiểu rõ phương pháp và rèn luyện cách trình bày lời giải khoa học để tránh mất điểm đáng tiếc.
Bài viết Giải Toán 9 trang 9 tập 2 Kết nối tri thức được biên soạn nhằm giúp học sinh tiếp cận bài học một cách nhẹ nhàng, logic và dễ hiểu, bám sát nội dung SGK. Thông qua hệ thống lời giải chi tiết, rõ ràng từng bước, bài viết không chỉ hỗ trợ học sinh hoàn thành bài tập trên lớp mà còn là tài liệu hữu ích phục vụ tự học tại nhà và ôn tập Toán 9 hiệu quả.
Bài 6.6 trang 9 Toán 9 Tập 2 Kết nối
Đề bài: Trong Hình 6.7 có hai đường cong là đồ thị của hai hàm số y = – 3x2 và y = x2. Hãy cho biết đường nào là đồ thị của hàm số y = – 3x2.
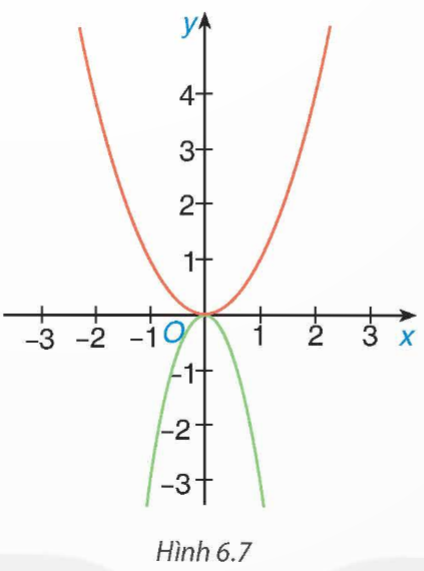
Hướng dẫn giải:
Vì hàm số y = – 3x2 có hệ số a = – 3 < 0 nên đồ thị của hàm số y = – 3x2 là đường cong màu xanh.
Bài 6.7 trang 9 Toán 9 Tập 2 Kết nối
Đề bài: Một cổng vòm được thiết kế dạng parabol y = ax2 như Hình 6.8. Biết chiều rộng của chân cổng là AB = 6 cm và chiều cao của cổng là OI = 4,5 cm.
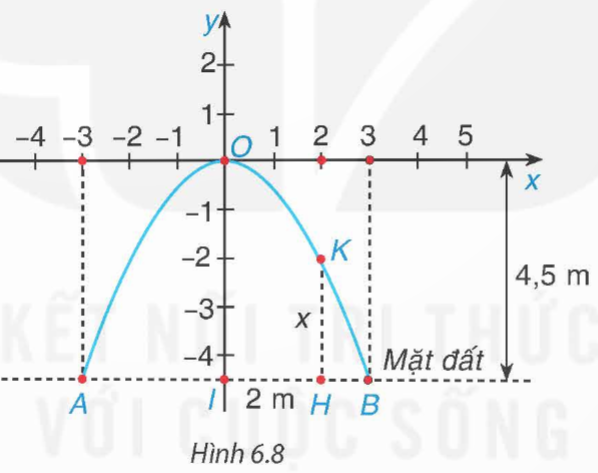
a) Tìm hệ số a dựa vào các dữ kiện trên. Từ đó, tính độ dài đoạn HK biết H cách điểm chính giữa cổng I là 2 m.
b) Để vận chuyển hàng qua cổng, người ta dự định sử dụng một xe tải có chiều rộng 2 m, chiều cao 3 m. Hỏi xe tải này có thể đi qua được cổng vòm đó hay không?
Hướng dẫn giải:
a) Trong Hình 6.8 ta thấy đồ thị hàm số y = ax2 đi qua điểm (3; 4,5)
⇒ 4,5 = a . 32
⇒ 4,5 = 9a
⇒ a = ![]()
Do đó HK = x = ![]() (m)
(m)
b) Do xe tải có chiều rộng 2 m nên ta tính chiều cao cổng tại vị trí cách I 1 m, tức x = 1.
Khi đó chiều cao cổng là ![]() m
m
Vì chiều cao cổng lớn hơn chiều cao của xe nên xe có thể qua được cổng vòm.
Bài học tiếp theo: Giải SGK Trang 10 Toán 9 Kết nối tri thức
-----------------------------------------------
Qua nội dung Giải SGK Toán 9 KNTT tập 2 trang 9, học sinh có thể củng cố lại kiến thức đã học, hiểu rõ bản chất từng dạng bài và từng bước hình thành tư duy giải Toán đúng chuẩn chương trình lớp 9. Việc tham khảo lời giải chi tiết không chỉ giúp kiểm tra kết quả mà còn giúp học sinh rút ra phương pháp làm bài nhanh, chính xác và hiệu quả hơn.
Đây là nguồn tài liệu phù hợp cho học sinh lớp 9 đang theo học chương trình Kết nối tri thức, đặc biệt hữu ích trong quá trình ôn tập thường xuyên và chuẩn bị cho kỳ thi vào lớp 10. Để học tốt Toán 9, học sinh nên kết hợp đọc kỹ lời giải, tự làm lại bài và theo dõi thêm các bài giải Toán 9 tập 2 khác để hệ thống hóa kiến thức một cách toàn diện.







