Toán 9 Kết nối tri thức Bài 28: Đường tròn ngoại tiếp và đường tròn nội tiếp của một tam giác

Bài 28 thuộc chương trình Toán 9 – Kết nối tri thức sẽ giúp học sinh hiểu rõ hơn về cách xác định tâm và bán kính của các đường tròn này, đồng thời vận dụng kiến thức để giải quyết các bài toán thực tiễn. Dưới đây là phần hướng dẫn giải chi tiết giúp các em nắm vững lý thuyết và rèn luyện kỹ năng giải bài tập hiệu quả.

Bài 9.7 trang 76 Toán 9 

Cho đường tròn (O) ngoại tiếp tam giác ABC. Tính bán kính của (O), biết rằng tam giác ABC vuông cân tại A và có cạnh bên bằng 2√2 cm.

Lời giải:

Vì ∆ABC cân tại A nên AB = AC = 2√2 cm.

Áp dụng định lí Pythagore vào ∆ABC vuông tại A, ta có:

BC2 = AB2 + AC2

Do đó BC2=(2√2)2+(2√2)2=16

Suy ra BC = 4 cm.

Vì O là tâm đường tròn ngoại tiếp tam giác ABC vuông tại A nên bán kính của (O) bẳng một nửa cạnh huyền BC.

Vậy bán kính của (O) là: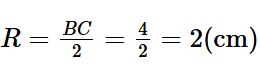

Bài 9.8 trang 76 Toán 9 

Cho tam giác đều ABC nội tiếp đường tròn (O). Biết rằng đường tròn (O) có bán kính bằng 3 cm. Tính diện tích tam giác ABC.

Lời giải:

Vì tam giác ABC đều nên tâm O của đường tròn ngoại tiếp tam giác là trọng tâm của tam giác đó và bán kính đường tròn ngoại tiếp tam giác là .

Theo bài, AO = 3 cm nên

Suy ra BC = 3√3 cm.

Gọi H là giao điểm của AO và BC. Khi đó AH vừa là đường trung trực, vừa là đường trung tuyến, cũng là đường cao của tam giác.

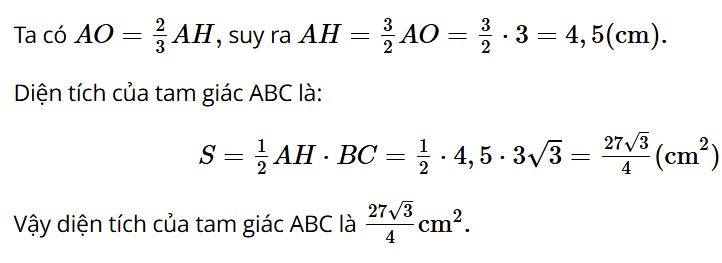
Bài 9.9 trang 76 Toán 9

Cho tam giác ABC nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC. Chứng minh rằng .

Lời giải:

Bài 9.10 trang 76 Toán 9

Cho đường tròn (I) nội tiếp tam giác ABC với các tiếp điểm trên các cạnh AB, AC lần lượt là E, F. Chứng minh rằng

Lời giải:

Vì đường tròn (I) nội tiếp tam giác ABC với các tiếp điểm trên các cạnh AB, AC lần lượt là E, F nên IE ⊥ AB và IF ⊥ AC.

 

 

 

 

 

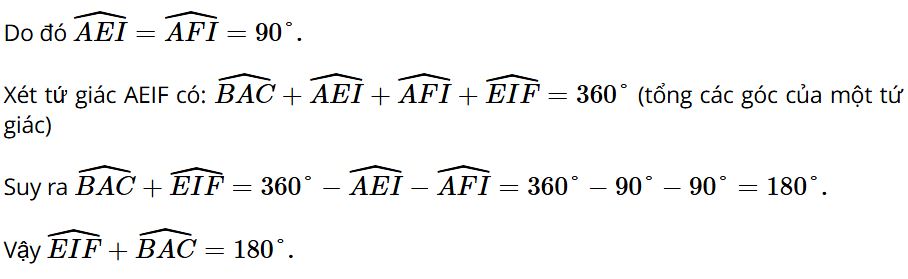
Bài 9.11 trang 76 Toán 9

Cho tam giác đều ABC ngoại tiếp đường tròn (I). Tính độ dài các cạnh của tam giác ABC biết rằng bán kính của (I) bằng 1 cm.

Lời giải:

Gọi độ dài các cạnh của tam giác đều ABC là a (cm).

Bài 9.12 trang 76 Toán 9

Người ta muốn làm một khung gỗ hình tam giác đều để đặt vừa khít một chiếc đồng hồ hình tròn có đường kính 30 cm (H.9.23). Hỏi độ dài các cạnh (phía bên trong) của khung gỗ phải bằng bao nhiêu?

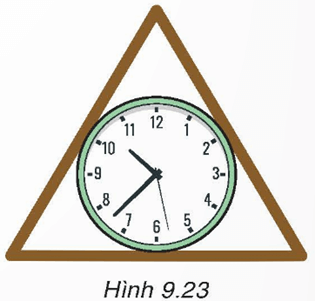
Lời giải:

Gọi độ dài các cạnh phía bên trong của khung gỗ là a (cm).

Bán kính của chiếc đồng hồ hình tròn là: r = 30 : 2 = 15 (cm).

Vì khung gỗ hình tam giác đều để đặt vừa khít chiếc đồng hồ nên đường tròn khung viền của đồng hồ nội tiếp tam giác chứa cạnh của khung gỗ và bán kính đường tròn này là

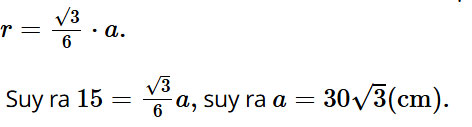
Vậy độ dài cạnh của tam giác (phía bên trong) của khung gỗ là 30√3 cm.