Giải Toán 9 trang 77 tập 1 Kết nối tri thức
Giải Toán 9 trang 77 Tập 1
Giải Toán 9 trang 77 tập 1 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Kết nối tri thức tập 1 trang 77.
Luyện tập 3 Trang 77 Toán 9 Tập 1
Cho tam giác vuông ABC có cạnh góc vuông AB = 4, cạnh huyền BC = 8. Tính cạnh AC (làm tròn đến chữ số thập phân thứ ba) và các góc B, C (làm tròn đến độ).
Hướng dẫn giải:
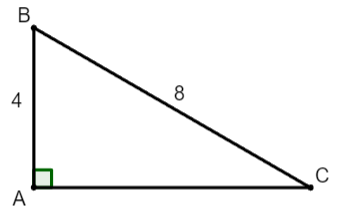
Xét tam giác ABC vuông tại A, ta có:
- AC2 = BC2 - AB2 = 82 - 42 = 48 (định lí Pythagore)
Suy ra AC ≈ 6,928
- Theo định nghĩa tỉ số lượng giác góc nhọn, ta có:
\(\cos B=\frac{AB}{BC}=\frac{4}{8}=\frac{1}{2}\); suy ra B = 60o.
- Do đó, \(\widehat{C} =90^{\circ} -\widehat{B}=90^{\circ} - 60^{\circ} =30^{\circ}\)
Luyện tập 4 Trang 77 Toán 9 Tập 1
Giải tam giác ABC vuông tại A, biết BC = 9, \(\widehat{C} =53^{\circ}\).
Hướng dẫn giải:
Xét tam giác ABC vuông tại A:
Ta có: \(\widehat{B} =90^{\circ} -\widehat{C}=90^{\circ} - 53^{\circ} =37^{\circ}\)
Theo định lí về hệ thức giữa cạnh huyền và cạnh góc vuông, ta có:
AB = BC . sin C = 9 . sin 53o ≈ 7,19
AC = BC . cos C = 9 . cos 53o ≈ 5,42
Vận dụng Trang 77 Toán 9 Tập 1
Giải bài toán ở tình huống mở đầu với α = 27o và β = 19o (làm tròn đến chữ số thập phân thứ hai).
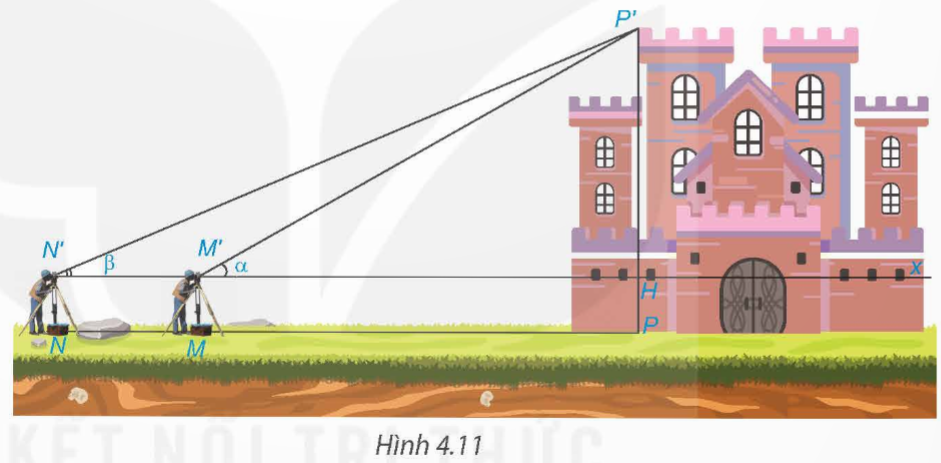
Bài toán: Để đo chiều cao của một toà lâu đài (H.4.11), người ta đặt giác kế thẳng đứng tại điểm M. Quay ống ngắm của giác kế sao cho nhìn thấy đỉnh P' của toà lâu đài dưới góc nhọn α. Sau đó, đặt giác kế thẳng đứng tại điểm N, NM = 20 m, thì nhìn thấy đỉnh P' dưới góc nhọn β (β < α). Biết chiều cao giác kế là 1,6 m, hãy tính chiều cao của toà lâu đài.
Hướng dẫn giải:
Ta có: N'H = P'H . cot β
M'H = P'H . cot α
Trừ từng vế của hai đẳng thức, ta có:
N'H - M'H = P'H(cot β - cot α)
⇔ 20 = P'H(cot β - cot α)
⇔ \(P'H=\frac{20}{\cotβ-\cot\alpha} =\frac{20}{\cot19^{\circ} -\cot27^{\circ} }\approx21,24\) m
Do đó, PP' = PH + HP' = 1,6 + 21,24 ≈ 22,84 m
Vậy chiều cao của tòa lâu đài khoảng 22,84 m.
-----------------------------------------------
---> Xem thêm: Giải Toán 9 trang 78 tập 1 Kết nối tri thức
Lời giải Toán 9 trang 77 Tập 1 Kết nối tri thức với các câu hỏi nằm trong Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng, được VnDoc biên soạn và đăng tải!
