Giải Toán 9 trang 8 tập 1 Kết nối tri thức
Giải Toán 9 trang 8 Tập 1
Giải Toán 9 trang 8 Tập 1 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Kết nối tri thức tập 1 trang 8.
Luyện tập 2 trang 8 SGK Toán 9 tập 1 KNTT
Viết nghiệm và biểu diễn hình học tất cả các nghiệm của mỗi phương trình bậc nhất hai ẩn sau:
a) 2x – 3y = 5
b) 0x + y = 3
c) x + 0y = − 2.
Hướng dẫn:
- Trong mặt phẳng tọa độ, tập hợp các điểm có tọa độ (x; y) thỏa mãn phương trình bậc nhất hai ẩn ax + by = c là một đường thẳng. Đường thẳng đó gọi là đường thẳng ax + by = c.
Lời giải chi tiết:
a) 2x – 3y = 5 (1)
Ta viết (1) dưới dạng 
\(y=\frac{2}{3}x-\frac{5}{3}\). Mỗi cặp số \(\left(x;\ \frac{2}{3}x-\frac{5}{3}\right)\) với x ∈ R tùy ý, là một nghiệm của (1).
Khi đó ta nói phương trình (1) có nghiệm (tổng quát) là:
\(\left(x;\ \frac{2}{3}x-\frac{5}{3}\right)\) với x ∈ R tùy ý.
Mỗi nghiệm này là tọa độ của một điểm thuộc đường thẳng \(y=\frac{2}{3}x-\frac{5}{3}\). Ta cũng gọi đường thẳng này là đường thẳng d: 2x − 3y = 5.
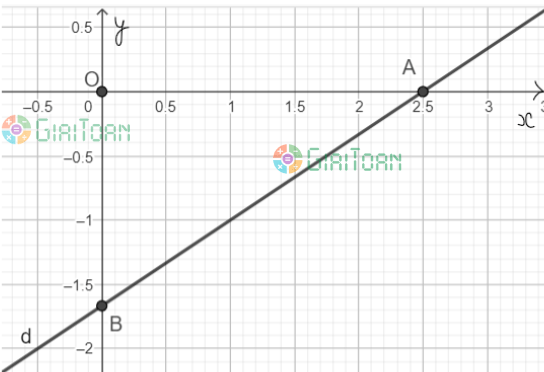
Ta xác định hai điểm tùy ý của d là A(\(\frac{5}{2}\); 0) và B(0; \(-\frac{5}{3}\)).
Ta biểu diễn hình học tất cả các nghiệm của phương trình bậc nhất hai ẩn 2x − 3y = 5 như sau:
b) 0x + y = 3 (2)
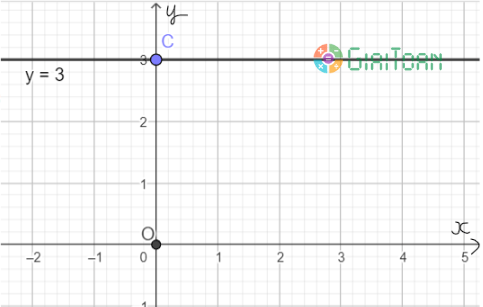
Ta viết gọn (2) thành y = 3. Phương trình (2) có nghiệm là (x; 3) với x ∈ R tùy ý.
Mỗi nghiệm này là tọa độ của một điểm thuộc đường thẳng song song với trục hoành và cắt trục tung tại điểm C(0; 3). Ta gọi đó là đường thẳng y = 3.
Ta biểu diễn hình học tất cả các nghiệm của phương trình bậc nhất hai ẩn 0x + y = 3 như sau:
c) x + 0y = − 2 (3)
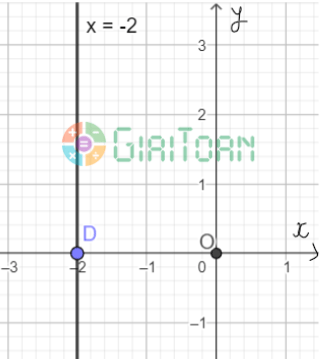
Ta viết gọn (3) thành x = − 2. Phương trình (3) có nghiệm là (− 2; y) với y ∈ R tùy ý.
Mỗi nghiệm này là tọa độ của một điểm thuộc đường thẳng song song với trục tung và cắt trục hoành tại điểm D(− 2; 0). Ta gọi đó là đường thẳng x = − 2.
Ta biểu diễn hình học tất cả các nghiệm của phương trình bậc nhất hai ẩn x + 0y = − 2 như sau:
-----------------------------------------------
---> Xem thêm: Giải Toán 9 trang 9 tập 1 Kết nối tri thức
---> Bài tiếp theo: Toán 9 Kết nối tri thức Bài 2: Giải hệ hai phương trình bậc nhất hai ẩn
Lời giải Toán 9 trang 8 Tập 1 Kết nối tri thức với các câu hỏi nằm trong Bài 1 Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn, được VnDoc biên soạn và đăng tải!
---> Tham khảo thêm: Đề thi giữa học kì 1 Toán 9 Kết nối tri thức.
