VnDoc.com

Giải Toán 9 trang 78 tập 1 Kết nối tri thức

Bài trước

Tải về

Bài sau

Giải Toán 9 trang 78 Tập 1

Bài 4.8 Trang 78 Toán 9 Tập 1
Bài 4.9 Trang 78 Toán 9 Tập 1
Bài 4.10 Trang 78 Toán 9 Tập 1
Bài 4.11 Trang 78 Toán 9 Tập 1
Bài 4.12 Trang 78 Toán 9 Tập 1
Bài 4.13 Trang 78 Toán 9 Tập 1

Giải Toán 9 trang 78 tập 1 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Kết nối tri thức tập 1 trang 78.

Bài 4.8 Trang 78 Toán 9 Tập 1

Giải tam giác ABC vuông tại A có BC = a, AC = b, AB = c, trong các trường hợp:

a) a = 21, b = 18

b) b = 10, $\widehat C = {30^{\circ} }$ $\hat{C} = 30^{\circ}$

c) c = 5, b = 3

Hướng dẫn giải:

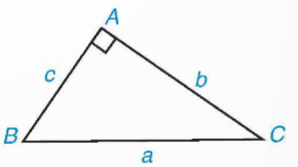
a) a = 21, b = 18

Xét tam giác ABC vuông tại A:

Ta có: a² = b² + c² (định lý Pythagore)

Suy ra: c² = a² - b² = 21² - 18² = 117 hay $c=3\sqrt{13}$ $c = 3 \sqrt{13}$

Ta có $\sin \widehat B = \frac{{b}}{{a}} = \frac{6}{7}$ $\sin \hat{B} = \frac{b}{a} = \frac{6}{7}$ nên B ≈ 59^o
$\widehat C = {90^0} - \widehat B = {90^0} - {59^0} \approx{31^0}$ $\hat{C} = 90^{0} - \hat{B} = 90^{0} - 59^{0} \approx 31^{0}$

b) b = 10, $\widehat C = {30^{\circ} }$ $\hat{C} = 30^{\circ}$

Xét tam giác ABC vuông tại A, ta có:

$\widehat B = {90^{\circ} } - \widehat C = {90^{\circ} } - {30^{\circ} } =60^{\circ}$ $\hat{B} = 90^{\circ} - \hat{C} = 90^{\circ} - 30^{\circ} = 60^{\circ}$
c = b . tan C = 10 . tan 30^o ≈ 6
$a= \frac{{b}}{{\sin B}} = \frac{{20}}{{\sin 60^{\circ} }} \approx 12$ $a = \frac{b}{\sin B} = \frac{20}{\sin 60^{\circ}} \approx 12$

c) c = 5, b = 3

Tam giác ABC vuông tại A, ta có:

a² = b² + c² = 3² + 5² = 34 (định lý Pythagore)

Suy ra $a= \sqrt {34}$ $a = \sqrt{34}$

Ta có $\tan B = \frac{{b}}{{c}} = \frac{3}{{5 }} \Rightarrow \widehat{B} \approx 31 ^{\circ}$ $\tan B = \frac{b}{c} = \frac{3}{5} \Rightarrow \hat{B} \approx 31^{\circ}$
$\widehat C = {90^{\circ} } - \widehat B= {90^{\circ} } - {31^{\circ} } =59^{\circ}$ $\hat{C} = 90^{\circ} - \hat{B} = 90^{\circ} - 31^{\circ} = 59^{\circ}$

Bài 4.9 Trang 78 Toán 9 Tập 1

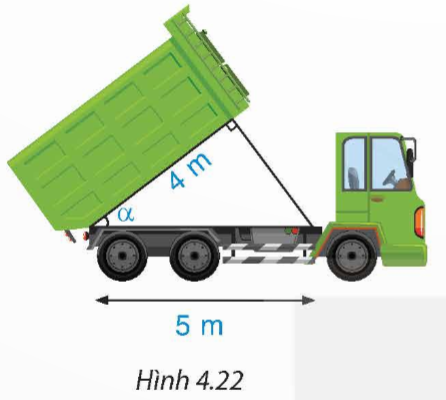
Tính góc nghiêng α của thùng xe chở rác trong Hình 4.22.

Hướng dẫn giải:

Theo định nghĩa tỉ số lượng giác côsin, ta có:

$\cosα= \frac45 =0,8$ $\cos α = \frac{4}{5} = 0, 8$ , suy ra α ≈ 36^o 52'

Vậy góc nghiêng α của thùng xe chở rác khoảng 36^o 52'.

Bài 4.10 Trang 78 Toán 9 Tập 1

Tìm góc nghiêng α và chiều rộng AB của mái nhà kho trong Hình 4.23 (góc làm tròn đến độ, độ dài làm tròn đến dm)

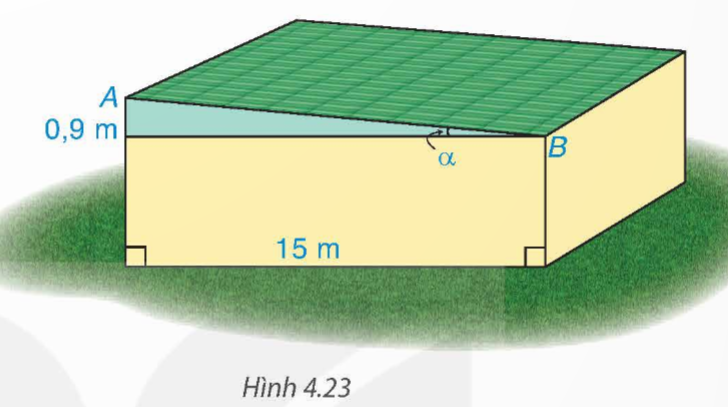
Hướng dẫn giải:

Ta có: $\tan \alpha = \frac{{0,9}}{{15}} = \frac{3}{50}\Rightarrow \alpha \approx 3^{\circ}$ $\tan α = \frac{0, 9}{15} = \frac{3}{50} \Rightarrow α \approx 3^{\circ}$

$AB=\frac{0,9}{\sin3^{\circ} } \approx 17,2$ $A B = \frac{0, 9}{\sin 3^{\circ}} \approx 17, 2$ m

Bài 4.11 Trang 78 Toán 9 Tập 1

Tính các góc của hình thoi có hai đường chéo dài $2\sqrt 3$ $2 \sqrt{3}$ và 2.

Hướng dẫn giải:

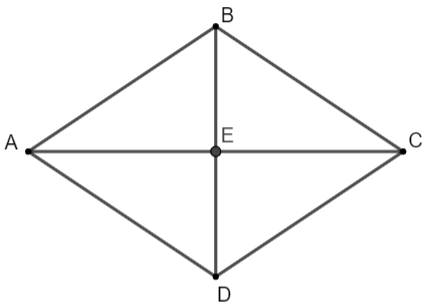
Gọi E là giao điểm của AC và BD

Do ABCD là hình thoi nên AC ⊥ BD và $BE = ED = \sqrt 3$ $B E = E D = \sqrt{3}$ ; AC = CB = 1

Xét tam giác ABE vuông tại E, ta có:

AB² = AE² + BE² = 4, suy ra AB = 2

Khi đó tam giác ABD là tam giác đều (tính chất hthoi)

Suy ra góc $\widehat {BAD} = \widehat {BCD} ={60^{\circ} }$ $\hat{B A D} = \hat{B C D} = 60^{\circ}$ và $\widehat {ABC} = \widehat {ADC} ={120^{\circ} }$ $\hat{A B C} = \hat{A D C} = 120^{\circ}$

Vậy hình thoi có một góc là 120⁰ và góc kia 60⁰.

Bài 4.12 Trang 78 Toán 9 Tập 1

Cho hình thang ABCD (AD // BC) có AD = 16 cm, BC = 4 cm và $\widehat A = \widehat B = \widehat {ACD} = {90^{\circ} }.$ $\hat{A} = \hat{B} = \hat{A C D} = 90^{\circ} .$

a) Kẻ đường cao CE của tam giác ACD. Chứng minh $\widehat {ADC} = \widehat {ACE}$ $\hat{A D C} = \hat{A C E}$ . Tính sin của các góc $\widehat {ADC},\widehat {ACE}$ $\hat{A D C}, \hat{A C E}$ và suy ra AC² = AE . AD. Từ đó tính AC.

b) Tính góc D của hình thang.

Hướng dẫn giải:

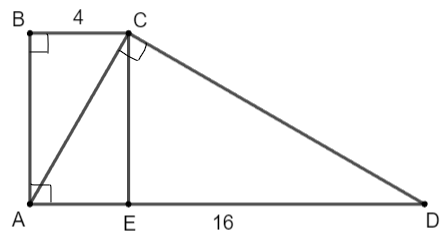
a) Ta có $\widehat {ADC} = \widehat {ACE}$ $\hat{A D C} = \hat{A C E}$ (cùng phụ với góc DCE)

Suy ra $\sin \widehat {ADC}=\sin \widehat {ACE}$ $\sin \hat{A D C} = \sin \hat{A C E}$

⇒ $\frac{{AC}}{{AD}} = \frac{{AE}}{{AC}}$ $\frac{A C}{A D} = \frac{A E}{A C}$

⇒ AC² = AE . AD

= 4 . 16 = 64 (AE = BC vì ABCE là hình chữ nhật)

Suy ra AC = 8 cm

b) Xét tam giác ADC vuông tại C, ta có:

$\sin \widehat {ADC}= \frac{{AC}}{{AD}} = \frac{8}{{16}} = \frac{1}{2}$ $\sin \hat{A D C} = \frac{A C}{A D} = \frac{8}{16} = \frac{1}{2}$

Suy ra $\widehat {ADC} = {30^{\circ} }$ $\hat{A D C} = 30^{\circ}$

Bài 4.13 Trang 78 Toán 9 Tập 1

Một người đứng tại điểm A, cách gương phẳng đặt nằm trên mặt đất tại điểm B là 1,2 m, nhìn thấy hình phản chiếu qua gương B của ngọn cây (cây mọc thẳng đứng, có gốc ở tại điểm C cách B là 4,8 m, B nằm giữa A và C). Biết khoảng cách từ mặt đất đến mắt người đó là 1,65 m. Tính chiều cao của cây (H.4.24).

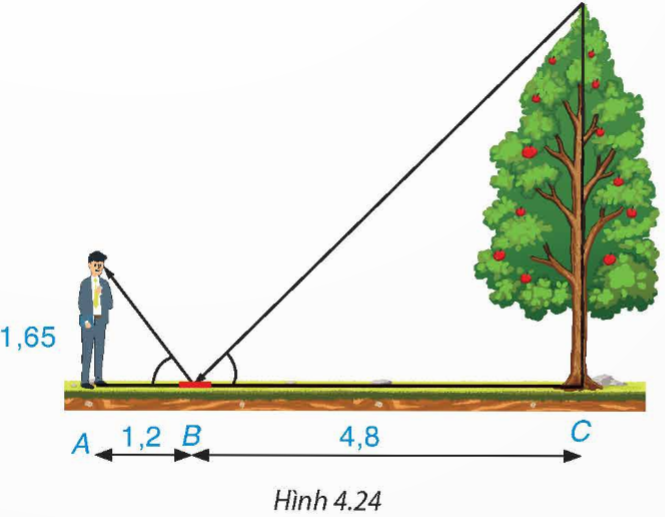
Hướng dẫn giải:

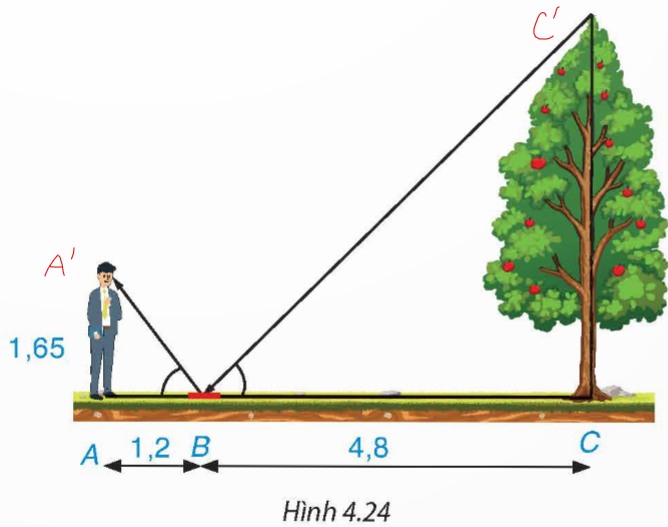
Theo quang học ta có $\widehat{ABA$ $\hat{A B A^{'}} = \hat{C B C^{'}}$

Do đó, $\tan \widehat {ABA$ $\tan \hat{A B A^{'}} = \tan \hat{C B C^{'}}$

⇒ $\frac{{1,65}}{{1,2}} = \frac{{CC$ $\frac{1, 65}{1, 2} = \frac{C C^{'}}{4, 8}$

suy ra $EC = \frac{{1,65}}{1,2}.4,8 = 6,6$ $E C = \frac{1, 65}{1, 2} .4, 8 = 6, 6$

Vậy chiều cao của cây là 6,6 m

-----------------------------------------------

---> Xem thêm: Giải Toán 9 trang 80 tập 1 Kết nối tri thức

Lời giải Toán 9 trang 78 Tập 1 Kết nối tri thức với các câu hỏi nằm trong Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng, được VnDoc biên soạn và đăng tải!

Chia sẻ, đánh giá bài viết

1

380

Bài trước

Bài sau

Chia sẻ bởi:
Lê Jelar

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

Tải tài liệu Trả phí + Miễn phí

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!