Giải Toán 9 trang 86 tập 1 Cánh diều
Giải Toán 9 trang 86 Tập 1
Giải Toán 9 trang 86 Tập 1 Cánh diều hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Cánh diều tập 1 trang 86.
Luyện tập 6 trang 86 Toán 9 Tập 1 Cánh diều
Cho hình chữ nhật ABCD thỏa mãn AC = 6 cm, 
\(\widehat {BAC} = 47^\circ\). Tính độ dài các đoạn thẳng AB, AD.
Hướng dẫn giải
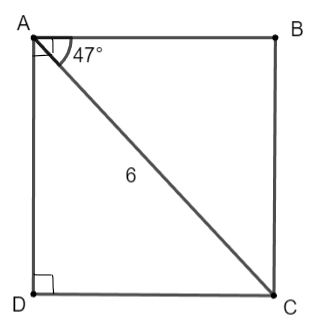
Xét tam giác ABC vuông tại B, ta có:
AB = AC . \(\cos \widehat {BAC}\) = 6 . cos 47o ≈ 4,1 (cm)
BC = AC . \(\sin \widehat {BAC}\) = 6 . sin 47o ≈ 4,4 (cm)
Vì ABCD là hình chữ nhật nên AD = BC ≈ 4,4 (cm)
Bài 1 trang 86 Toán 9 Tập 1 Cánh diều
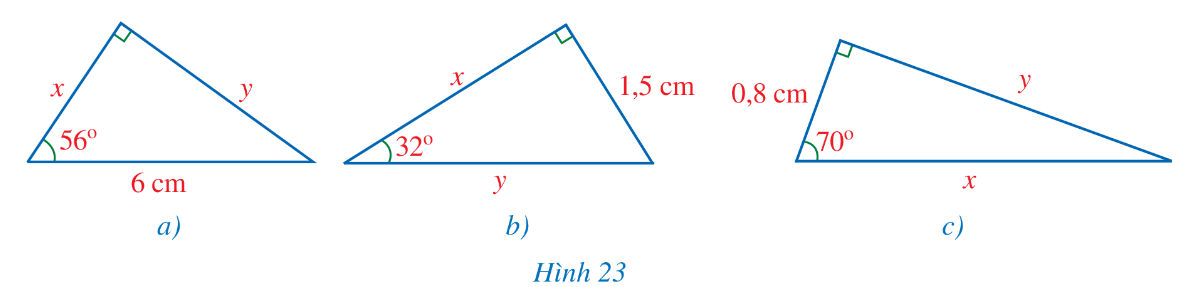
Tìm x, y trong mỗi hình 23a, 23b, 23c (làm tròn kết quả đến hàng phần mười của centimét).
Hướng dẫn giải
Hình 23a):
x = 6 . cos 56o ≈ 3,4 (cm)
y = 6 . sin 56o ≈ 4,9 cm
Hình 23b):
x = 1,5 . cot 32o ≈ 2,4 cm
\(y=\sqrt{1,5^2+2,4^2}\approx2,8\) cm
Hình 23c):
y = 0,8 . tan 70o ≈ 2,2 cm
\(x=\sqrt{0,8^2+2,2^2}\approx2,3\) cm
Bài 2 trang 86 Toán 9 Tập 1 Cánh diều
Cho tam giác ABC có đường cao AH = 6 cm, \(\widehat B = 40^\circ , \ \widehat C = 35^\circ\). Tính độ dài các đoạn thẳng AB, BH, AC, BC (làm tròn kết quả đến hàng phần mười của centimét).
Hướng dẫn giải
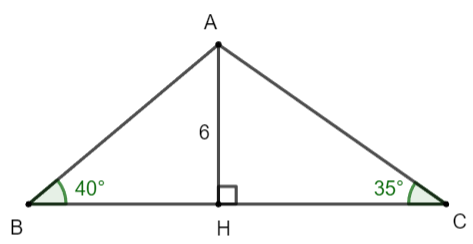
Do tam giác ABH vuông tại H nên:
\(AB = \frac{{AH}}{{\sin 40^\circ }} = \frac{6}{{\sin 40^\circ }} \approx 9,3\) (cm)
BH = AH . cot 40o ≈ 7,2 (cm)
Do tam giác ACH vuông tại H nên:
\(AC = \frac{{AH}}{{\sin 35^\circ }} = \frac{6}{{\sin 35^\circ }} \approx 10,5\left( {cm} \right).\)
CH = AH . cot 35o ≈ 8,6 (cm)
Do đó BC = BH + CH ≈ 7,2 + 8,6 ≈ 15,8 (cm)
Bài 3 trang 86 Toán 9 Tập 1 Cánh diều
Cho tam giác ABC vuông tại A có \(\widehat {B} =30^{\circ}\). Chứng minh \(AC=\frac{1}{2}BC\).
Hướng dẫn giải
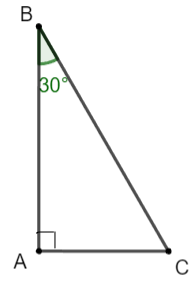
Do tam giác ABC vuông tại A nên:
AC = BC . sin B = BC . sin 30o = BC . \(\frac{1}{2}\)
Vậy \(AC=\frac{1}{2}BC\).
-----------------------------------------------
---> Trang tiếp theo: Giải Toán 9 trang 87 tập 1 Cánh diều
Lời giải Toán 9 trang 86 Tập 1 Cánh diều với các câu hỏi nằm trong Bài 2: Một số hệ thức về cạnh và góc trong tam giác vuông, được VnDoc biên soạn và đăng tải!
