Giải Toán 9 trang 100 tập 1 Cánh diều
Giải Toán 9 trang 100 Tập 1
Giải Toán 9 trang 100 Tập 1 Cánh diều hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Cánh diều tập 1 trang 100.
Bài 2 trang 100 Toán 9 Tập 1 Cánh diều
Xác định vị trí tương đối của hai đường tròn (O) và (O’) trong mỗi hình 17a, 17b, 17c, 17d:
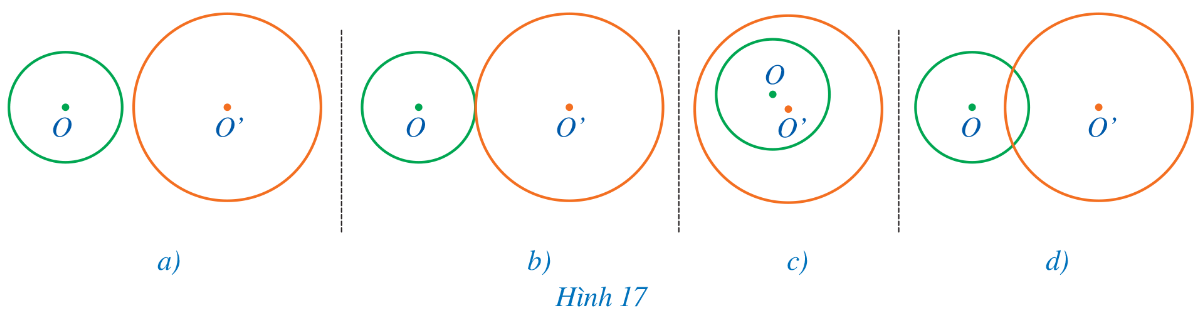
Hướng dẫn giải
a) Hai đường tròn (O) và (O') ở ngoài nhau.
b) Hai đường tròn (O) và (O') tiếp xúc ngoài.
c) Đường tròn (O') đựng đường tròn (O).
d) Hai đường tròn (O) và (O') cắt nhau.
Bài 3 trang 100 Toán 9 Tập 1 Cánh diều
Cho đoạn thẳng MN và đường thẳng a là đường trung trực của đoạn thẳng MN. Điểm O thuộc đường thẳng a.
a) Vẽ đường tròn tâm O bán kính R = OM.
b) Chứng minh điểm N thuộc đường tròn (O; R).
Hướng dẫn giải
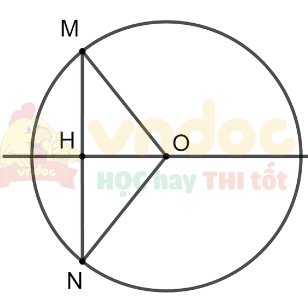
b) Ta có O thuộc a nên OM = ON
Mà OM = R nên ON = R
Do đó N thuộc đường tròn (O; R).
Bài 4 trang 100 Toán 9 Tập 1 Cánh diều
Cho đường tròn (O; R) và dây AB = R. Tính số đo góc AOB.
Hướng dẫn giải
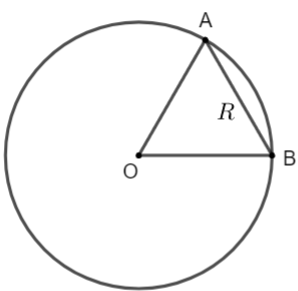
Ta có AB là dây cung nên OA = OB = R
Do đó tam giác OAB là tam giác đều.
Suy ra ![]() \(\widehat{AOB}=60^{\circ}\).
\(\widehat{AOB}=60^{\circ}\).
Bài 5 trang 100 Toán 9 Tập 1 Cánh diều
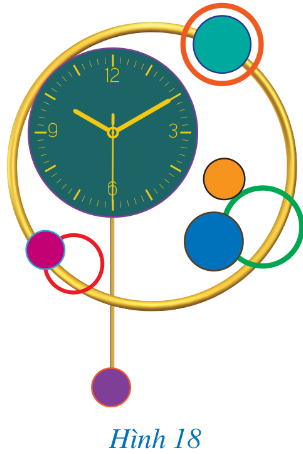
Chiếc đồng hồ trang trí ở Hình 18 gợi nên vị trí tương đối của các đường tròn. Quan sát Hình 18 và chỉ ra một cặp đường tròn:
|
a) Cắt nhau b) Tiếp xúc ngoài c) Tiếp xúc trong d) Không giao nhau |
 |
Hướng dẫn giải
a) Đường tròn màu xanh lá và đường tròn màu vàng cắt nhau.
b) Đường tròn màu xanh lá và đường tròn màu cam tiếp xúc ngoài.
c) Đường tròn màu vàng và đường tròn khung đồng hồ tiếp xúc trong.
d) Đường tròn màu xanh lá và đường tròn màu đỏ không giao nhau.
Bài 6 trang 100 Toán 9 Tập 1 Cánh diều
Cho đường tròn (O; R) và dây AB khác đường kính. Gọi M là trung điểm của AB.
a) Đường thẳng OM có phải là đường trung trực của đoạn thẳng AB hay không? Vì sao?
b) Tính khoảng cách từ điểm O đến đường thẳng AB, biết R = 5 cm, AB = 8 cm.
Hướng dẫn giải
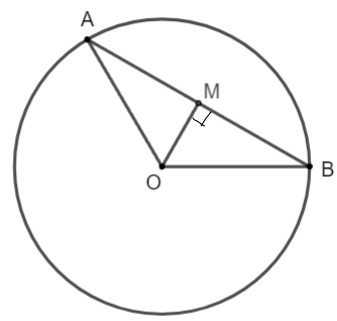
a) Ta có: MA = MB (gt) và OA = OB = R
Suy ra OM là đường trung trực của đoạn thẳng AB.
b) Do OM là đường trung trực của AB nên OM ⊥ AB.
Xét tam giác AOM vuông tại M, ta có:
OA2 = OM2 + MA2 (định lí Pythagore)
Suy ra OM2 = OA2 - MA2 = 52 - 42 = 9
Vậy OM = 3 cm.
Bài 7 trang 100 Toán 9 Tập 1 Cánh diều
Cho hai đường tròn cùng tâm (O; R), (O; r) với R > r. Các điểm A, B thuộc đường tròn (O; R), các điểm A', B' thuộc đường tròn (O; r) sao cho O, A, A' thẳng hàng; O, B, B' thẳng hàng và điểm O không thuộc đường thẳng AB. Chứng minh:
a) ![]() \(\frac{OA'}{OA}=\frac{OB'}{OB}\)
\(\frac{OA'}{OA}=\frac{OB'}{OB}\)
b) AB // A'B'.
Hướng dẫn giải
Đang cập nhật...
-----------------------------------------------
---> Trang tiếp theo: Giải Toán 9 trang 101 tập 1 Cánh diều
Lời giải Toán 9 trang 100 Tập 1 Cánh diều với các câu hỏi nằm trong Bài 1: Đường tròn. Vị trí tương đối của hai đường tròn, được VnDoc biên soạn và đăng tải!









