Toán 9 Cánh diều Bài 5: Độ dài cung tròn, diện tích hình quạt tròn, diện tích hình vành khuyên
Giải Toán 9 Cánh diều Bài 5: Độ dài cung tròn, diện tích hình quạt tròn, diện tích hình vành khuyên hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Cánh diều tập 1 trang 118, 119, 120, 121, 122, 123.
Giải Toán 9 Cánh diều tập 1 trang 118, 119, 120, 121, 122, 123.
Giải Toán 9 trang 118
Hoạt động 1 trang 118 Toán 9 Tập 1:
Lấy một vòng tròn không dãn có dạng hình tròn (Hình 66a), cắt vòng dây và kéo thẳng vòng dây đó để nhận được sợi dây như ở Hình 66b.
Đo chiều dài sợi dây đó.
Ta nói chiều dài sợi dây bằng chu vi của đường tròn.
Hướng dẫn giải:
HS thực hiện hoạt động theo hướng dẫn của GV và SGK.
Luyện tập 1 trang 118 Toán 9 Tập 1:
Tính chu vi của đường tròn bán kính 5 cm (theo đơn vị centimet và làm tròn kết quả đến hàng phần mười).
Hướng dẫn giải:
Chu vi của đường tròn là: C = 2π.5 = 10π ≈ 31,4 (cm).
Giải Toán 9 trang 119
Hoạt động 2 trang 119 Toán 9 Tập 1:
a) Đánh dấu hai điểm A, B trên một vòng dây không dãn có dạng đường tròn (Hình 67a), cắt cung AB của vòng dây và kéo thẳng cung đó để nhận được sợi dây như ở Hình 67b.
Đo chiều dài sợi dây đó.
Ta nói chiều dài sợi dây bằng độ dài của cung tròn AB.
b) Ta coi mỗi đường tròn bán kính R là một cung tròn có số đo 360°. Chia đường tròn đó thành 360 phần bằng nhau, mỗi phần là cung tròn có số đo bằng 1°; chu vi của đường tròn khi đó cũng được chia thành 360 phần bằng nhau. Tính theo R:
⦁ Độ dài của cung có số đo 1°;
⦁ Độ dài của cung có số đo n°.
Hướng dẫn giải:
a) HS thực hiện hoạt động theo hướng dẫn của GV và SGK.
b) Độ dài của cung tròn có số đo 360° chính là chu vi của đường tròn bán kính R và bằng 2πR.
Độ dài của cung có số đo 1° là: 
\(\frac{2πR}{360} =\frac{πR}{180}\)
Độ dài của cung có số đo n° là \(n⋅\frac{πR}{180} =\frac{πRn}{180}\)
Hoạt động 3 trang 119 Toán 9 Tập 1:
Vẽ đường tròn (O; 2 cm) và các điểm A, B thỏa mãn OA < 2 cm, OB = 2 cm. Nêu nhận xét về vị trí các điểm A, B so với đường tròn (O; 2 cm).
Hướng dẫn giải:
Ta có:
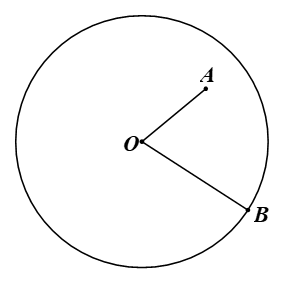
⦁ OA < 2 cm nên A nằm trong đường tròn (O; 2 cm);
⦁ OB = 2 cm nên B nằm trên đường tròn (O; 2 cm).
Giải Toán 9 trang 120
Hoạt động 4 trang 120 Toán 9 Tập 1:
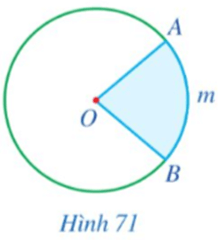
Quan sát Hình 71, hãy cho biết phần hình tròn (O) tô màu xanh được giới hạn bởi hai bán kính và cung nào?
Hướng dẫn giải:
Phần hình tròn (O) tô màu xanh được giới hạn bởi hai bán kính OA, OB và cung AmB.
Giải Toán 9 trang 122
Hoạt động 6 trang 122 Toán 9 Tập 1:
a) Hình 80 mô tả một phần bản vẽ của chi tiết máy. Hình đó giới hạn bởi mấy đường tròn cùng tâm?
b) Hãy vẽ một hình tương tự Hình 80 bằng cách vẽ các đường tròn (O; 2 cm) và (O; 3 cm). Tính hiệu diện tích của hai hình tròn đó.
Hướng dẫn giải:
a) Hình chi tiết máy được giới hạn bởi hai đường tròn cùng tâm.
b)
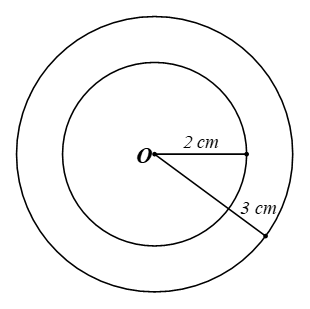
Diện tích hình tròn tâm O bán kính 3 cm là: π.32 = 9π (cm2).
Diện tích hình tròn tâm O bán kính 2 cm là: π.22 = 4π (cm2).
Hiệu diện tích của hai hình tròn đó là: 9π – 4π = 5π (cm2).
Giải Toán 9 trang 122
Luyện tập 5 trang 122 Toán 9 Tập 1:
Tính diện tích của hình vành khuyên đó giới hạn bởi hai đường tròn cùng tâm và có bán kính lần lượt là 2,5 cm; 2 cm.
Hướng dẫn giải:
Hình vành khuyên giới hạn bởi hai đường tròn cùng tâm O và có bán kính lần lượt là 2,5 cm; 2 cm được tô màu xanh như hình vẽ dưới đây:
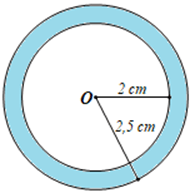
Diện tích của hình vành khuyên tô màu xanh là: S=π(2,52−22)=\(\frac{9π}{4}\)(cm2).
Bài 1 trang 122 Toán 9 Tập 1:
Quan sát các hình 83, 84, 85, 86.
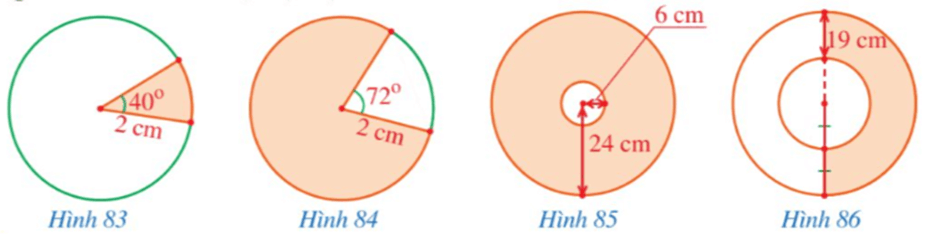
a) Tính diện tích phần được tô màu mỗi hình đó.
b) Tính độ dài cung tròn được tô màu xanh ở mỗi hình 83, 84.
Giải Toán 9 trang 123
Bài 2 trang 123 Toán 9 Tập 1:
Hình87 mô tả mặt cắt của chiếc đèn led có dạng hình vành khuyên màu trắng với bán kính các đường tròn lần lượt là 15 cm, 18 cm, 21 cm, 24 cm. Tính diện tích hai hình vành khuyên đó.
Hướng dẫn giải:
Diện tích hình vành khuyên bên trong là: S1 = π(182 – 152) = 99π (cm2).
Diện tích hình vành khuyên bên ngoài là S1 = π(242 – 212) = 135π (cm2).
Bài 3 trang 123 Toán 9 Tập 1:
Hình 88 mô tả mặt cắt của một khung gỗ có dạng ghép của năm hình: hai nửa hình tròn đường kính 2 cm; hai hình chữ nhật kích thước 2 cm × 8 cm (Hình 88b); một phần tư hình vành khuyên giới hạn bởi hai đường tròn cùng tâm có bán kính lần lượt là 4 cm và 6 cm. Tính diện tích của mặt cắt của khung gỗ đó.
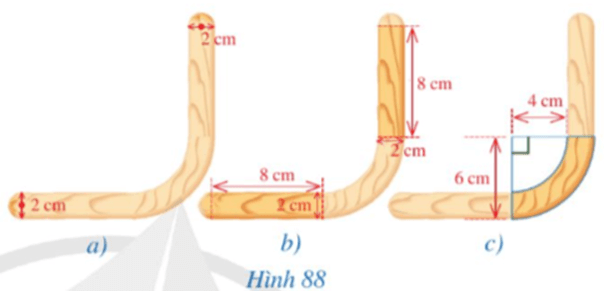
Hướng dẫn giải:
Tổng diện tích hai nửa hình tròn đường kính 2 cm (bán kính 1 cm) chính là diện tích của một hình tròn bán kính 1 cm, và bằng: S1 = π.12 = π (cm2).
Tổng diện tích hai hình chữ nhật kích thước 2 cm × 8 cm là: S2 = 2.(2.8) = 32 (cm2).
Diện tích một phần tư hình vành khuyên giới hạn bởi hai đường tròn cùng tâm có bán kính lần lượt là 4 cm và 6 cm là:
S3=\(\frac{1}{4}\)⋅π(62−42)=5π(cm2).
Diện tích của mặt cắt của khung gỗ đó là:
S = S 1 + S 2 + S 3 = π + 32 + 5π = 6π + 32 (cm 2 ).
Bài 4 trang 123 Toán 9 Tập 1:
Khi đóng đáy thuyền cho những con thuyền vượt biển, người Vikings sử dụng hai loại nêm: nêm góc và nêm cong (lần lượt tô màu xanh, màu đỏ trong Hình 89). Mặt cắt ABCD của nêm góc có dạng hai tam giác vuông OAE, ODE bằng nhau với cạnh huyền chung và bỏ đi hình quạt tròn OBC (Hình 90), được làm từ những thân cây mọc thẳng. Mặt cắt MNPQ của nêm cong có dạng một phần của hình vành khuyên (Hình 91), được làm từ những thân cây cong. Kích thước của nêm cong được cho như ở Hình 91.
a) Diện tích của nêm cong là bao nhiêu centimét vuông (lấy 1 ft = 30,48 cm, 1 in = 2,54 cm và làm tròn kết quả đến hàng đơn vị)?
b) Cần phải biết những kích thước nào của nêm góc để tính được diện tích của nêm đó?
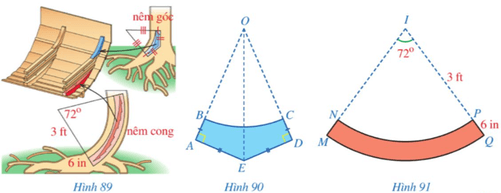
Hướng dẫn giải:
a)
+ Diện tích quạt tròn \(INP\) là:
\(S = \frac{{\pi {R^2}n}}{{360}} = \frac{{\pi {{.90}^2}.72}}{{360}} = 1620\pi \approx 5087\left( {c{m^2}} \right)\)
+ Diện tích quạt tròn \(IMQ\) là:
\(S = \frac{{\pi {R^2}n}}{{360}} = \frac{{\pi {{\left( {6.2,54.30.3} \right)}^2}.72}}{{360}} = \frac{{\pi .1371,{6^2}.72}}{{360}} \approx 1181448\left( {c{m^2}} \right)\)
+ Diện tích của nêm cong là:
\(S = {S_{IMQ}} - {S_{INP}} \approx 1181448 - 5087 \approx 1176361\left( {c{m^2}} \right)\)
b) Để tính được nêm góc cần biết: diện tích hình \(OAD\), góc \(AOD\), độ dài cạnh \(OB\)
