Giải Toán 9 trang 95 tập 1 Cánh diều
Giải Toán 9 trang 95 Tập 1
Giải Toán 9 trang 95 Tập 1 Cánh diều hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Cánh diều tập 1 trang 95.
Luyện tập 2 trang 95 Toán 9 Tập 1 Cánh diều
Cho tam giác nhọn ABC. Đường tròn tâm O đường kính BC cắt các cạnh AB và AC lần lượt tại M và N. Chứng minh MN < BC.
Hướng dẫn giải
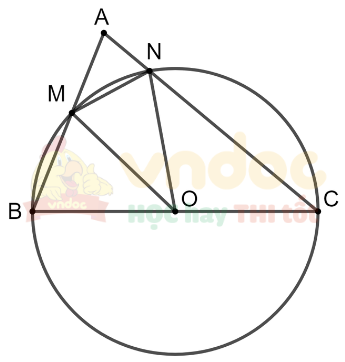
a) Xét tam giác OMN ta có:
MN < OM + ON (bất đẳng thức tam giác) (1)
b) Ta có: OB = OM = ON = OC = R
Suy ra OM + ON = OB + OC (2)
Từ (1) và (2) suy ra MN < BC
Hoạt động 3 trang 95 Toán 9 Tập 1 Cánh diều
Cho đường tròn (O; R).
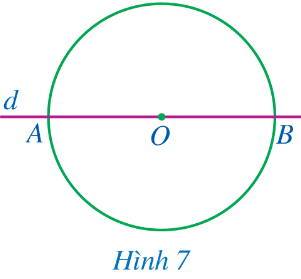
a) Vẽ đường thẳng d đi qua tâm O cắt đường tròn tại A, B. So sánh OA và OB (Hình 7).
b) Giả sử M là một điểm tùy ý trên đường tròn (O; R). Trên tia đối của tia OM, ta lấy điểm N sao cho ON = OM. Điểm N có thuộc đường tròn (O; R) hay không?
Hướng dẫn giải
a) Do A và B cùng thuộc đường tròn (O; R) nên OA = OB = R
b) Ta có: OM = R (M thuộc đường tròn)
Mà OM = ON (gt) nên OM = ON = R
Suy ra N cũng thuộc đường tròn (O; R).
Hoạt động 4 trang 95 Toán 9 Tập 1 Cánh diều
Cho đường tròn (O; R). Giả sử d là đường thẳng đi qua tâm O, M là một điểm tùy ý trên đường tròn (O; R). Kẻ MH vuông góc với d tại H. Trên tia MH lấy điểm N sao cho H là trung điểm của MN (ta gọi điểm N là điểm đối xứng với điểm M qua đường thẳng d). Điểm N có thuộc đường tròn (O; R) hay không?
Hướng dẫn giải
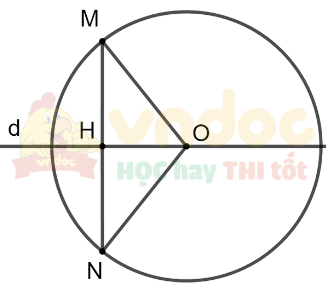
Xét tam giác vuông OMH và tam giác giác ONH ta có:
MH = NH (gt)
OH chung
Do đó ∆ OMH = ∆ ONH (cgv - cgv)
Suy ra OM = ON (hai cạnh tương ứng)
Mà OM = R (M thuộc đường tròn) nên ON = R
Do đó N thuộc đường tròn (O; R).
-----------------------------------------------
---> Trang tiếp theo: Giải Toán 9 trang 96 tập 1 Cánh diều
Lời giải Toán 9 trang 95 Tập 1 Cánh diều với các câu hỏi nằm trong Bài 1: Đường tròn. Vị trí tương đối của hai đường tròn, được VnDoc biên soạn và đăng tải!









