Toán 9 Cánh diều Bài 2: Tứ giác nội tiếp đường tròn

Giải Toán 9 Cánh diều Bài 2: Tứ giác nội tiếp đường tròn sẽ hướng dẫn giải chi tiết từng bài tập, giúp học sinh ôn tập hiệu quả, chuẩn bị tốt cho các bài kiểm tra và kỳ thi. 

Giải Bài 1 trang 78

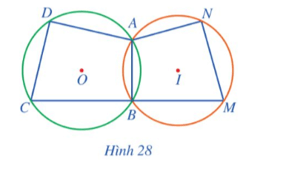
Quan sát Hình 28 và cho biết trong hai đường tròn (O) và (I), đường tròn nào ngoại tiếp tứ giác ABCD, đường tròn nào ngoại tiếp tứ giác ABMN.

Lời giải:

Ở Hình 28:

⦁ đường tròn (O) ngoại tiếp tứ giác ABCD vì đường tròn (O) đi qua các đỉnh A, B, C, D của tứ giác ABCD;

⦁ đường tròn (I) ngoại tiếp tứ giác ABMN vì đường tròn (I) đi qua các đỉnh A, B, M, N của tứ giác ABMN.

Bài 2 trang 78 

Cho tứ giác ABCD nội tiếp đường tròn. Tính số đo các góc còn lại của tứ giác đó trong mỗi trường hợp sau:

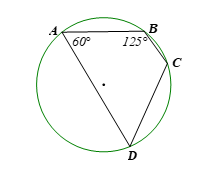
a)\(\widehat A = 60^\circ ,\widehat B = 125^\circ\) .

b) \(\widehat B = 95^\circ ,\widehat C = 67^\circ\).

c) \(\widehat C = 75^\circ ,\widehat D = 115^\circ\) .

d) \(\widehat D = 103^\circ ,\widehat A = 117^\circ\) .

Giải

Vì tứ giác ABCD nội tiếp đường tròn nên tổng 2 góc đối bằng 180^\circ , do đó ta có: \(\widehat A + \widehat C = 180^\circ ,\widehat B + \widehat D = 180^\circ\) .

a) \(\widehat A + \widehat C = 180^\circ suy ra \widehat C = 180^\circ - \widehat A = 180^\circ - 60^\circ = 120^\circ\).

\(\widehat B + \widehat D = 180^\circ suy ra \widehat D = 180^\circ - \widehat B = 180^\circ - 125^\circ = 55^\circ .\)

b) \(\widehat B + \widehat D = 180^\circ suy ra \widehat D = 180^\circ - \widehat B = 180^\circ - 95^\circ = 85^\circ .\)

\(\widehat A + \widehat C = 180^\circ suy ra \widehat C = 180^\circ - \widehat A = 180^\circ - 67^\circ = 113^\circ .\)

c)\(\widehat A + \widehat C = 180^\circ suy ra \widehat A = 180^\circ - \widehat C = 180^\circ - 75^\circ = 105^\circ .\)

\(\widehat B + \widehat D = 180^\circ suy ra \widehat B = 180^\circ - \widehat D = 180^\circ - 115^\circ = 65^\circ .\)

d)\(\widehat B + \widehat D = 180^\circ suy ra \widehat B = 180^\circ - \widehat D = 180^\circ - 103^\circ = 77^\circ .\)

\(\widehat A + \widehat C = 180^\circ suy ra \widehat C = 180^\circ - \widehat A = 180^\circ - 117^\circ = 63^\circ .\)

Bài 3 trang 78

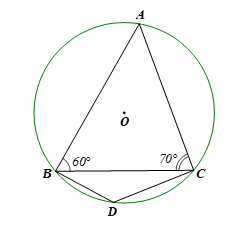
Cho tam giác ABC nội tiếp đường tròn (O) thỏa mãn \(\widehat {ABC} = 60^\circ ,\widehat {ACB} = 70^\circ\) . Giả sử D là điểm thuộc cung BC không chứa A (D khác B và C). Tính số đo góc BDC.

Lời giải chi tiết

Áp dụng Định lý tổng 3 góc trong tam giác ABC có:

\(\begin{array}{l}\widehat {ABC} + \widehat {BCA} + \widehat {CAB} = 180^\circ \\\widehat {CAB} = 180^\circ - \widehat {ABC} - \widehat {BCA}\\\widehat {CAB} = 180^\circ - 60^\circ - 70^\circ \\\widehat {CAB} = 50^\circ .\end{array}\)

Vì tứ giác ABDC nội tiếp đường tròn nên tổng 2 góc đối bằng 180^\circ , do đó ta có:

\(\begin{array}{l}\widehat A + \widehat D = 180^\circ \\\widehat D = 180^\circ - \widehat A\\\widehat D = 180^\circ - 50^\circ \\\widehat D = 130^\circ .\end{array}\)

Vậy \(\widehat {BDC} = 130^\circ\) .

Giải bài 4 trang 78

Mặt trên của tấm đệm có dạng hình tròn ở Hình 29 gợi nên hình ảnh đường tròn ngoại tiếp hình chữ nhật. Biết hình chữ nhật đó có chiều rộng, chiều dài lần lượt là 3 dm, 5 dm. Tính độ dài đường kính mặt trên của tấm đệm, từ đó tính diện tích mặt trên của tấm đệm.

Giải

Mặt trên của tấm nệm được biểu diễn bằng hình học như sau:

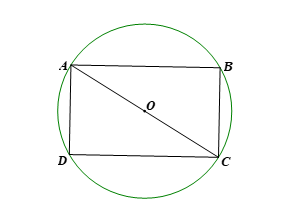
Hình chữ nhật ABCD có chiều dài AB = 5 dm, chiều rộng BC = 3 dm.

Xét tam giác ACB vuông tại B có:

\(\begin{array}{l}A{B^2} + B{C^2} = A{C^2}(Pytago)\\{5^2} + {3^2} = A{C^2}\\AC = \sqrt {34} dm\end{array}\)

Mà hình chữ nhật ABCD nội tiếp đường tròn nên đường kính tấm đệm là \(AC = \sqrt {34} dm\).

Diện tích hình tròn là: \(S = \pi .\frac{{{d^2}}}{4} = \pi .\frac{{{{\sqrt {34} }^2}}}{4} = \frac{{17\pi }}{2}d{m^2}.\)

Bài 5 trang 78

Cho hình thang ABCD (AB // CD) nội tiếp đường tròn. Chứng minh rằng hình thang ABCD là hình thang cân.

Giải

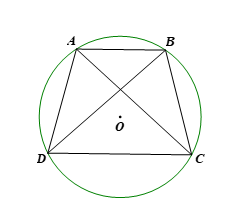
Ta có: ABCD nội tiếp đường tròn nên \(\widehat A + \widehat C = 180^\circ\) . Hơn nữa \(\widehat A + \widehat D = 180^\circ (do AB//CD)\)

Suy ra \(\widehat C = \widehat D\).

Xét hình thang ABCD có AB//CD, \(\widehat C = \widehat D\) nên ABCD là hình thang cân (dhnb).

Bài 6 trang 78

Cho tứ giác nội tiếp ABCD có hai đường chéo AC và BD cắt nhau tại I.

a) Hai góc ABD và ACD có bằng nhau hay không? Vì sao?

b) Chứng minh \(\Delta AIB\backsim \Delta IDC\) và IA.IC = IB.ID.

Giải

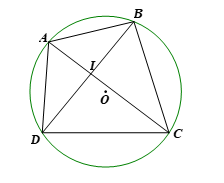
a) Do tứ giác ABCD nội tiếp đường tròn nên \(\widehat {ACD} = \widehat {ABD}\)(cùng chắn cung AD).

b) Xét tam giác AIB và tam giác DIC có:

\(\widehat {AIB} = \widehat {DIC}\) (đối đỉnh)

\(\widehat {ACD} = \widehat {ABD}(cmt)\)

\(Nên \Delta AIB\backsim \Delta DIC(g.g)\)

Suy ra\(\frac{{IA}}{{ID}} = \frac{{IB}}{{IC}} hay IA.IC = IB.ID (đpcm)\)

Bài 7 trang 78

Cho tứ giác nội tiếp ABCD có tam giác ABC là tam giác nhọn. Hai đường cao AM và CN của tam giác ABC cắt nhau tại H (Hình 30).

a) \(\widehat {MHN} + \widehat {ABC} = 180^\circ .\)

b) \(\widehat {AHC} = \widehat {ADC.}\)

c) \(\widehat {ADC} = \widehat {BAM} + 90^\circ\).

Giải

a) Do tam giác ABC có hai đường cao AM, CN nên \(\widehat {HMB} = 90^\circ ,\widehat {BNH} = 90^\circ\)

Xét tứ giác HMBN có:

\(\begin{array}{l}\widehat {NHM} + \widehat {HMB} + \widehat {MBN} + \widehat {BNH} = 360^\circ \\\widehat {NHM} + \widehat {MBN} = 360^\circ - \widehat {HMB} - \widehat {BNH}\\\widehat {NHM} + \widehat {MBN} = 360^\circ - 90^\circ - 90^\circ = 180^\circ .\end{array}\)

Hay \(\widehat {MHN} + \widehat {ABC} = 180^\circ\) .

b) Vì ABCD nội tiếp đường tròn nên \(\widehat {CDA} + \widehat {ABC} = 180^\circ .\)

mà \(\widehat {MHN} + \widehat {ABC} = 180^\circ\) (câu a)

suy ra \(\widehat {CDA} = \widehat {MHN}\), hơn nữa \(\widehat {CHA} = \widehat {MHN}\) (đối đỉnh)

vậy \(\widehat {CHA} = \widehat {CDA.}\)

c) Xét tam giác AMB vuông tại M có: \(\widehat {BAM} + \widehat {AMB} = \widehat {BAM} + 90^\circ = 180^\circ - \widehat {MBA.}\)

Mà \(180^\circ - \widehat {MBA} = \widehat {ADC}\) (do ABCD nội tiếp)

Vậy \(\widehat {ADC} = \widehat {BAM} + 90^\circ\).