Toán 9 Cánh diều Bài tập cuối chương 8
Giải bài tập cuối chương 8 Toán 9 sách Cánh diều sẽ hướng dẫn giải chi tiết từng bài tập, giúp học sinh củng cố kiến thức về hình không gian đã học hình trụ, hình nón, hình cầu và các công thức tính diện tích, thể tích của chúng. Hãy cùng ôn luyện thật kỹ để nắm vững kiến thức và đạt kết quả cao trong học tập nhé!
Mục lục bài viết
Bài 1 trang 79 SGK Toán 9 tập 2 - Cánh diều
Đề bài:
Cho tứ giác ABCD nội tiếp đường tròn có 
\(\hat{C} = 80^{\circ}\). Số đo góc A là:
A.\(80^{\circ}\)
B. \(160^{\circ}\)
C. \(40^{\circ}\)
D.\(100^{\circ}\)
Giải
Ta có tứ giác ABCD nội tiếp đường tròn nên \(\hat{A} + \hat{C} = 180^{\circ}\), do đó \(\hat{A} = 180^{\circ} - \hat{C} = 180^{\circ} - 80^{\circ} = 100^{\circ}.\)
Chọn đáp án D.
Bài 2 trang 79 SGK Toán 9 tập 2 - Cánh diều
Cho đường tròn (I) nội tiếp tam giác ABC và lần lượt tiếp xúc với các cạnh BC, CA, AB tại M, N, P. Chứng minh: \(\widehat{AIN} = \widehat{PMN} = \frac{1}{2}\widehat{PIN}\).
Lời giải:
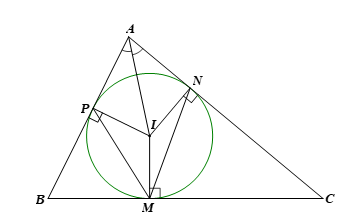
Vì đường tròn (I) lần lượt tiếp xúc với các cạnh CA, AB tại N, P nên AC, AB là hai tiếp tuyến của (I) cắt nhau tại A.
Do đó IA là phân giác của góc PIN (tính chất hai tiếp tuyến cắt nhau).
Suy ra \(\widehat{AIN} = \frac{1}{2}\widehat{PIN}\). (1)
Xét đường tròn (I) có \(\widehat{PIN} và \widehat{PMN}\)lần lượt là góc ở tâm và góc nội tiếp cùng chắn cung PN nên \(\widehat{PMN} = \frac{1}{2}\widehat{PIN}\). (2)
Từ (1) và (2) suy ra\(\widehat{AIN} = \widehat{PMN} = \frac{1}{2}\widehat{PIN}\).
Bài 3 trang 79 Toán 9 Tập 2
Cho tam giác nhọn ABC nội tiếp đường tròn (O). Các đường cao AK, BM cắt nhau tại trực tâm H của tam giác ABC. Tia AK cắt đường tròn (O) tại điểm N (khác A). Chứng minh:
a) \(\widehat{CBM} = \widehat{CAK}\);
b) Tam giác BHN cân;
c) BC là đường trung trực của HN.
Lời giải:
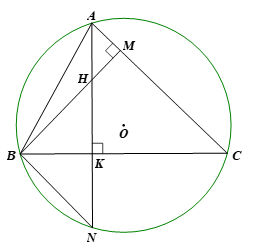
a) Xét \(\triangle ABC\) có các đường cao AK, BM cắt nhau tại trực tâm H nên \(AK \perp BC và BM \perp AC\).
Vì\(\triangle AKC\) vuông tại K có \(\widehat{KAC} + \widehat{C} = 90^{\circ}\) (tổng hai góc nhọn của tam giác vuông bằng \(90^{\circ})\).
Vì\(\triangle BMC\) vuông tại M có \(\widehat{CBM} + \widehat{C} = 90^{\circ}\) (tổng hai góc nhọn của tam giác vuông bằng \(90^{\circ}\)).
Suy ra \(\widehat{CBM} = \widehat{CAK}\).
b) Xét đường tròn (O) có \(\widehat{CAN} và \widehat{CBN}\) là hai góc nội tiếp cùng chắn cung CN nên \(\widehat{CAN} = \widehat{CBN} hay \widehat{CAK} = \widehat{KBN}\).
Mà \(\widehat{CBM} = \widehat{CAK}\)(câu a) nên \(\widehat{KBN} = \widehat{CBM} hay \widehat{KBN} = \widehat{KBH}\).
Do đó BK là đường phân giác của góc HBN.
Xét \(\triangle BHN\) có đường cao BK đồng thời là đường phân giác nên \(\triangle BHN\) cân tại B.
c) Vì \(\triangle BHN\) cân tại B (câu b) nên đường cao BK đồng thời là đường trung trực của HN.
Vậy BC là đường trung trực của HN.
Bài 4 trang 79 Toán 9 Tập 2
Cho tứ giác nội tiếp ABCD có hai tia CD và BA cắt nhau tại I. Chứng minh:
a) \(\widehat{IAD} = \widehat{BCD}\);
b) \(IA \cdot IB = IC \cdot ID\).
Lời giải:
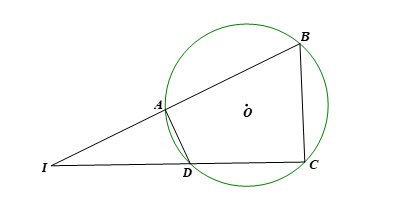
a) Vì tứ giác ABCD nội tiếp đường tròn nên các góc đối diện có tổng số đo bằng \(180^{\circ}\).
Do đó: \(\widehat{BAD} + \widehat{BCD} = 180^{\circ}\).
Mà \(\widehat{BAD} + \widehat{IAD} = 180^{\circ}\) (hai góc kề bù).
Suy ra \(\widehat{IAD} = \widehat{BCD}\).
b) Xét \(\triangle IAD và \triangle ICB\), có:\(\widehat{IAD} = \widehat{ICD} (do \widehat{IAD} = \widehat{BCD}) và \widehat{BIC}\) là góc chung.
Do đó \(\triangle IAD \sim \triangle ICB (g.g)\).
Suy ra \(\frac{IA}{IC} = \frac{ID}{IB}\)(tỉ số đồng dạng).
Từ đó, \(IA \cdot IB = IC \cdot ID\).
Bài 5 trang 79 Toán 9 Tập 2
Cho tứ giác ABCD và các điểm M, N lần lượt thuộc các đoạn thẳng AB và CD sao cho các tứ giác AMND, BMNC là các tứ giác nội tiếp. Chứng minh \(\widehat{A} + \widehat{B} = 180^{\circ}\).
Lời giải:
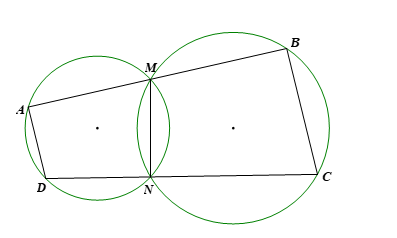
Tứ giác AMND là tứ giác nội tiếp nên \(\widehat{MAD} + \widehat{MND} = 180^{\circ}\) (tổng hai góc đối nhau của tứ giác nội tiếp bằng \(180^{\circ}\)).
Tứ giác BMNC là tứ giác nội tiếp nên \(\widehat{MBC} + \widehat{MNC} = 180^{\circ}\) (tổng hai góc đối nhau của tứ giác nội tiếp bằng \(180^{\circ}\)).
Suy ra \(\widehat{MAD} + \widehat{MND} + \widehat{MBC} + \widehat{MNC} = 180^{\circ} + 180^{\circ} = 360^{\circ}\).
Lại có \(\widehat{MND} + \widehat{MNC} = 180^{\circ}\) (hai góc kề bù).
Nên \(\widehat{MAD} + \widehat{MBC} = 360^{\circ} - (\widehat{MND} + \widehat{MNC}) = 360^{\circ} - 180^{\circ} = 180^{\circ}\).
Vậy \(\widehat{A} + \widehat{B} = 180^{\circ}\).
Bài 6 trang 79 Toán 9 Tập 2
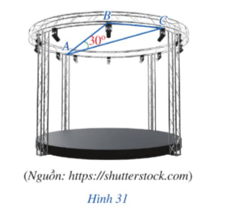
Khung thép của một phần sân khấu có dạng đường tròn bán kính 15 m. Mắt của một người thợ ở vị trí A nhìn hai đèn ở các vị trí B, C (A, B, C cùng thuộc đường tròn bán kính 15 m), bằng cách nào đó, người thợ thấy rằng góc nhìn \(\widehat{BAC} = 30^{\circ}\) (Hình 31). Khoảng cách giữa hai vị trí B, C bằng bao nhiêu mét?
Lời giải:
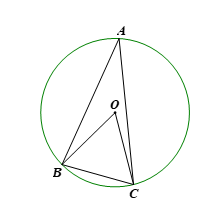
Gọi O là tâm đường tròn bán kính 15 m.
Xét đường tròn (O) có \(\widehat{BOC} và \widehat{BAC}\) lần lượt là góc ở tâm và góc nội tiếp cùng chắn cung BC nên \(\widehat{BAC} = \frac{1}{2}\widehat{BOC}, suy ra \widehat{BOC} = 2\widehat{BAC} = 2 \cdot 30^{\circ} = 60^{\circ}\).
Xét \(\triangle OBC\) có OB = OC = 15 m (vì B và C cùng nằm trên đường tròn (O; 15 m)) và \(\widehat{BOC} = 60^{\circ} nên \triangle OBC\) là tam giác đều.
Suy ra BC = OB = 15 m.
Vậy khoảng cách giữa hai vị trí B, C bằng 15 mét.
