Toán 9 Cánh diều Đường tròn ngoại tiếp tam giác, đường tròn nội tiếp tam giác
Giải Toán 9 Cánh diều Đường tròn ngoại tiếp tam giác, Đường tròn nội tiếp tam giác sẽ hướng dẫn giải chi tiết từng bài tập, giúp học sinh ôn tập hiệu quả, chuẩn bị tốt cho các bài kiểm tra và kỳ thi.
Mục lục bài viết
Bài 1 trang 73
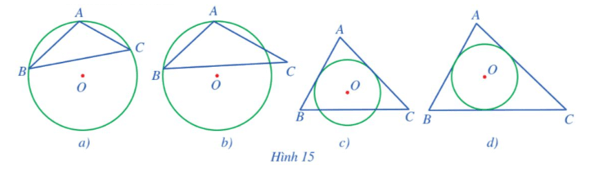
Trong các hình 15a, 15b, 15c, 15d, ở hình nào ta có đường tròn (O) là đường tròn ngoại tiếp tam giác ABC? Ở hình nào ta có đường tròn (O) là đường tròn nội tiếp tam giác ABC? Vì sao?
Lời giải:
⦁ Ở Hình 15a, đường tròn (O) là đường tròn ngoại tiếp tam giác ABC, vì đường tròn (O) đi qua cả ba đỉnh A, B, C của tam giác ABC.
⦁ Ở Hình 15b, đường tròn (O) không là đường tròn ngoại tiếp tam giác ABC vì nó không đi qua đỉnh C của tam giác ABC.
⦁ Ở Hình 15c, đường tròn (O) không là đường tròn nội tiếp tam giác ABC, vì nó không tiếp xúc với cạnh BC.
⦁ Ở Hình 15d, đường tròn (O) là đường tròn nội tiếp tam giác ABC, vì nó tiếp xúc với ba cạnh AB, BC, CA của tam giác ABC.
Bài 2 trang 74
Tính bán kính đường tròn ngoại tiếp tam giác ABC vuông tại A, biết AB = 5 cm, AC = 12 cm.
Giải
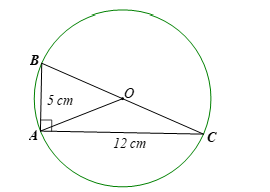
Xét ∆ABC vuông tại A, theo định lí Pythagore, ta có:
BC2 = AB2 + AC2 = 52 + 122 = 169.
Suy ra BC = 13 (cm).
Mặt khác, đường tròn ngoại tiếp tam giác vuông ABC có tâm là trung điểm O của cạnh huyền BC và bán kính bằng nửa cạnh huyền BC.
Vậy bán kính đường tròn ngoại tiếp tam giác ABC vuông tại A là
\(\frac{BC}{2}=\frac{13}{2}=6,5cm\)
Bài 3 trang 74
Cho bán kính đường tròn nội tiếp tam giác đều bằng 4 cm. Tính cạnh của tam giác đều đó.
Giải
Giả sử đường tròn (I; 4 cm) nội tiếp tam giác đều ABC có cạnh bằng a (cm). Khi đó AB = a (cm).
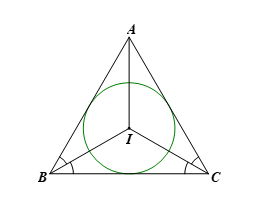
Vì tam giác ABC đều ngoại tiếp đường tròn (I; 4 cm) nên ta có \(4=\frac{a\sqrt{3}}{6}\) (cm).
Suy ra \(a=\frac{4\times6}{\sqrt{3}}=8\sqrt{3}(cm).\)
Vậy A B = 8 √ 3 cm .
Bài 4 trang 74
Một chiếc máy quay ở đài truyền hình được đặt trên giá đỡ ba chân, các điểm tiếp xúc với mặt đất của ba chân lần lượt là ba đỉnh A, B, C của tam giác đều ABC (Hình 10). Tính khoảng cách giữa hai vị trí A và B, biết bán kính đường tròn ngoại tiếp tam giác ABC là 4 dm.
Giải
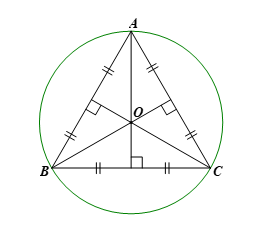
Giả sử tam giác ABC đều có cạnh bằng a (dm) nội tiếp đường tròn (O; 4 dm).
Khi đó AB = a (dm).
Vì tam giác đều ABC nội tiếp đường tròn (O) nên ta có \(4=\frac{a\sqrt{3}}{3}\) (dm).
Suy ra \(a=\frac{4\times3}{\sqrt{3}}=4\sqrt{3}\) (dm).
Vậy A B = 4 √ 3 dm .
Giải bài tập 5 trang 74 SGK
Giải bài tập 5 trang 74 SGK
Cho tam giác nhọn ABC (AB<AC) nội tiếp đường tròn (O) đường kính AD = 2R. Gọi M là trung điểm của cạnh BC và H là trực tâm của tam giác ABC. Chứng minh:
a) \(BD \bot AB,CD \bot AC.\)
b) Tứ giác BHCD là hình bình hành.
c) \(A{C^2} + B{H^2} = 4{R^2}\).
d) Ba điểm H, M, D thẳng hàng và AH = 2OM.
Giải
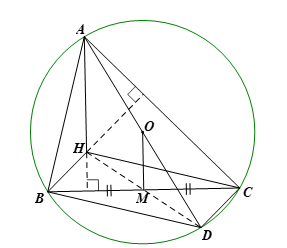
a) Chứng minh: \(BD \bot AB\)
Vì tam giác ABD nội tiếp đường tròn (O) nên AO = OB = OD Mà AD là đường kính của (O) suy ra \(OA = OD = \frac{{AD}}{2}\).
Do đó \(OB = OA = OD = \frac{{AD}}{2}\).
Xét tam giác ABD có đường trung tuyến BO và \(OB = \frac{{AD}}{2}\) nên tam giác ABD vuông tại B, suy ra \(BD \bot AB\)
Chứng minh: \(CD \bot AC\).
Vì tam giác ACD nội tiếp đường tròn (O) nên AO = OC = OD Mà AD là đường kính của (O) suy ra \(OA = OD = \frac{{AD}}{2}\).
Do đó \(OC = OA = OD = \frac{{AD}}{2}\).
Xét tam giác ACD có đường trung tuyến CO và \(OC = \frac{{AD}}{2}\) nên tam giác ACD vuông tại C, suy ra \(CD \bot AC\).
b) Ta có: H là trực tâm của tam giác ABC nên \(BH \bot AC,CH \bot AB\)
Ta lại có:
\(BH \bot AC, CD \bot AC(câu a) nên BH // DC.\)
\(CH \bot AB, BD \bot AB\) (câu a) nên CH // BD.
Xét BHCD có: BH // DC, CH // BD (cmt) suy ra BHCD là hình bình hành (dhnb).
c) Do BHCD là hình bình hành nên BH = CD.
Xét tam giác ADC vuông tại C có: \(A{C^2} + C{D^2} = A{D^2}\), mà BH = CD, AD = 2R nên:
\(A{C^2} + B{H^2} = 4{R^2}\).
d) Do BHCD là hình bình hành, M là trung điểm của đường chéo BC nên M cũng là trung điểm của đường chéo HD. Hay H, M, D thẳng hàng.
Xét tam giác AHD có: M là trung điểm của HD (cmt), O là trung điểm của AD nên OM là đường trung bình, suy ra \(OM = \frac{1}{2}AH\) hay AH = 2OM.
Bài 6 trang 74
Cho tứ giác ABCD có các tam giác ABC và ACD lần lượt ngoại tiếp các đường tròn (I) và (K) sao cho hai đường tròn này cùng tiếp xúc với đường thẳng AC tại điểm H thuộc đoạn thẳng AC. Giả sử đường tròn (I) tiếp xúc với cạnh AB tại M, đường tròn (K) tiếp xúc với cạnh AD tại N (Hình 17). Chứng minh:
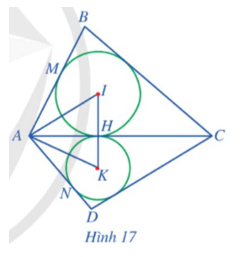
a) Ba điểm I, H, K thẳng hàng.
b) AM = AN.
c) \(\widehat {IAK} = \frac{1}{2}\widehat {BAD}\).
Giải
a) Do đường tròn (I) nội tiếp tam giác ABC và tiếp xúc với đường thẳng AC tại H nên \(IH \bot AC\), suy ra \(\widehat {IHA} = 90^\circ\) .
Do đường tròn (K) nội tiếp tam giác ADC và tiếp xúc với đường thẳng AC tại H nên\(KH \bot AC\), suy ra \(\widehat {IHK} = 90^\circ\) .
Ta có: \(\widehat {IHA} + \widehat {AHK} = \widehat {IHK} = 90^\circ + 90^\circ = 180^\circ\), nên I, H, K thẳng hàng.
b) Xét đường tròn (I) có hai tiếp tuyến AB, AC cắt nhau tại A nên AM = AH (tính chất hai tiếp tuyến cắt nhau)
Xét đường tròn (K) có hai tiếp tuyến AC, AD cắt nhau tại A nên AN = AH (tính chất hai tiếp tuyến cắt nhau)
Suy ra AM = AN ( = AH).
c) Xét đường tròn (I) có hai tiếp tuyến AB, AC nên AI là phân giác của góc BAC suy ra \(\widehat {IAH} = \frac{1}{2} \widehat {BAC}\)
Xét đường tròn (K) có hai tiếp tuyến AC, AD nên AK là phân giác của góc DAC suy ra \(\widehat {KAH} = \frac{1}{2} \widehat {DAC}\)
Ta có:
\(\widehat {IAK} = \widehat {IAH} + \widehat {KAH}
= \frac{1}{2} \widehat {BAC} + \frac{1}{2} \widehat {DAC}
= \frac{1}{2} (\widehat {BAC} + \widehat {DAC})
= \frac{1}{2}\widehat {BAD}.
Hay \widehat {IAK} = \frac{1}{2}\widehat {BAD}.\)
