Liên hệ giữa phép nhân và phép khai phương
Chuyên đề Toán học lớp 9: Liên hệ giữa phép nhân và phép khai phương được VnDoc sưu tầm và giới thiệu tới các bạn tham khảo. Tài liệu tổng hợp lý thuyết kèm bài tập vận dụng cho các em tham khảo luyện tập, sẽ giúp các bạn học sinh học tốt môn Toán học lớp 9 hơn. Mời các bạn tham khảo.
Chuyên đề: Liên hệ giữa phép nhân và phép khai phương
A. Lý thuyết Liên hệ giữa phép nhân và phép khai phương
1. Căn bậc hai của một tích
Với hai biểu thức A và B không âm, ta có ![]()
Ví dụ:
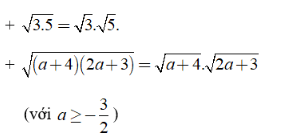
Chú ý: Định lý có thể mở rộng với nhiều số không âm
Ví dụ: Tính
a) √(4.9) b) √(1.16) c) √(9.81) d) √(16.25)
Giải:
a) Ta có: √(4.9) = √4. √9 = 2.3 = 6
b) Ta có: √(1.16) = √1. √16 = 1.4 = 4
c) Ta có: √(9.81) = √9. √81 = 3.9 = 27
d) Ta có: √(16.25) = √16. √25 = 4.5 = 20
2. Căn bậc hai của một thương
Với biểu thức A không âm, biểu thức B dương ta có: 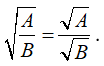
Ví dụ:
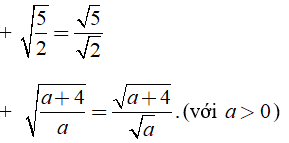
3. Áp dụng
+ Quy tắc khai phương một tích
Muốn khai phương một tích của các số không âm, ta có thể khai phương từng thừa số rồi nhân các kết quả lại với nhau
+ Quy tắc nhân các căn bậc hai
Muốn nhân các căn bậc hai của các số không âm, ta có thể nhân các số dưới căn với nhau rồi khai phương kết quả đó.
Ví dụ 1: Áp dụng quy tắc khai phương một tích, hãy tính:
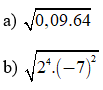
Giải:
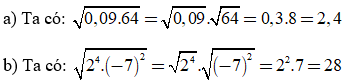
Ví dụ 2: Áp dụng quy tắc nhân, hãy tính:
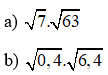
Giải:
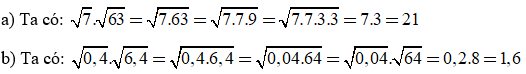
Ví dụ 3: Rút gọn biểu thức ![]() với a ≥ 3
với a ≥ 3
Giải:
![]()
B. Trắc nghiệm & Tự luận
I. Bài tập trắc nghiệm
Câu 1: Kết quả rút gọn của biểu thức 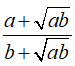 (với a, b > 0) là?
(với a, b > 0) là?
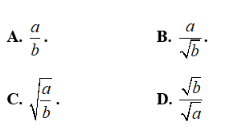
Với a, b > 0, ta có
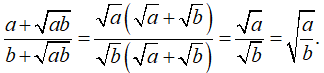
Chọn đáp án C.
Câu 2: Cho 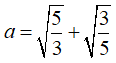 , giá trị của biểu thức
, giá trị của biểu thức 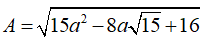 là ?
là ?
A. 4. B. 2√2. C. 1. D. √2.
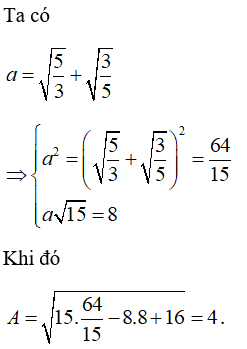
Chọn đáp án A.
Câu 3: Giá trị của biểu thức 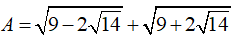 là?
là?
A. 2√2. B. 2√7. C. √14. D. √2.
Ta có
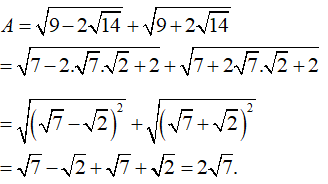
Chọn đáp án B.
Câu 4: Giá trị lớn nhất của biểu thức ![]() là?
là?
A. 2. B. 1 C. 2√2 D. 4.
Tập xác định D = [2; 4]
Áp dụng BĐT Bunhia – copxki ta có:
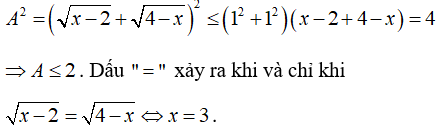
Chọn đáp án A.
II. Bài tập tự luận
Câu 1: Thực hiện các phép tính sau:
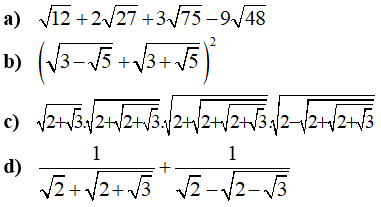
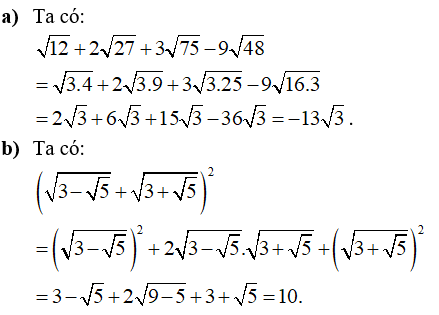
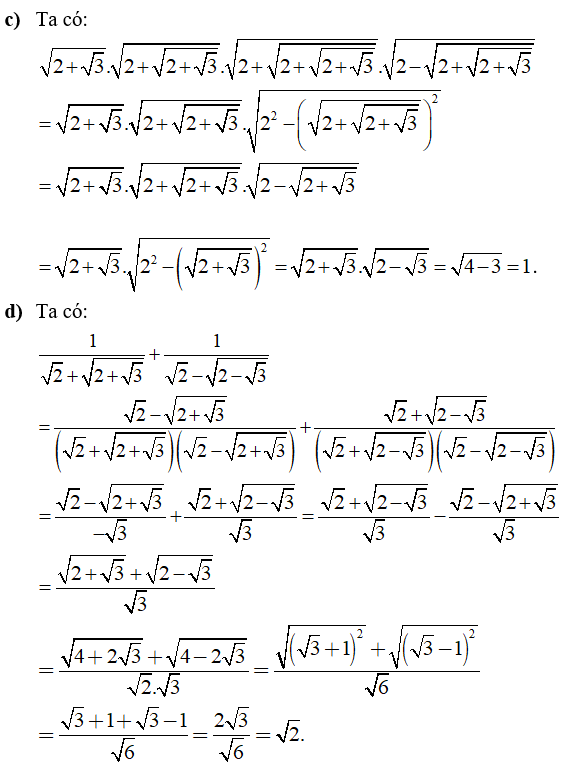
Câu 2: Cho biểu thức
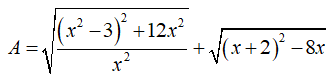
a) Rút gọn A
b) Tìm giá trị nguyên của x để giá trị của A là một số nguyên
a) Điều kiện: x ≠ 0.
Ta có
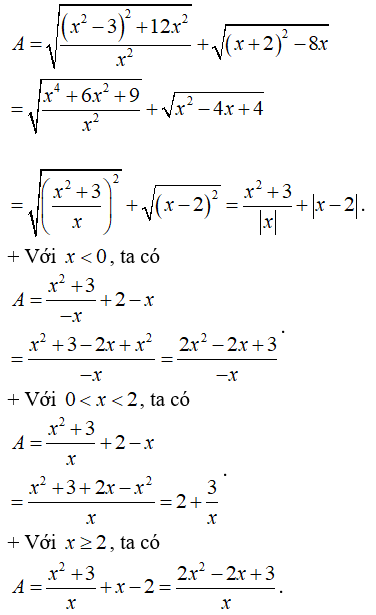
b) Từ kết quả trên, giá trị A nguyên khi và chỉ khi 3/x nguyên.
3/2 nguyên khi 3 chia hết cho x ⇒ x ∈ {±1; ±3}.
Câu 3: Giải các phương trình sau:
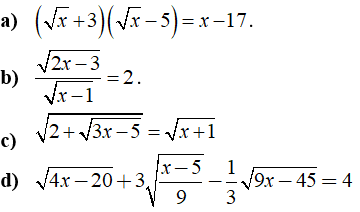
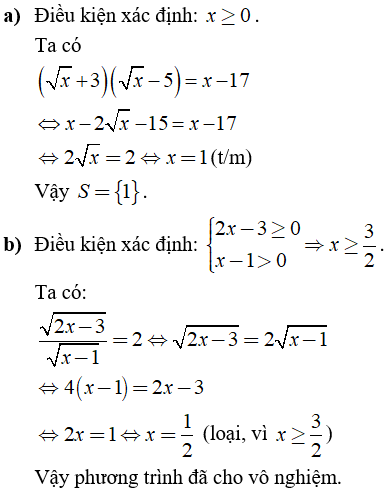
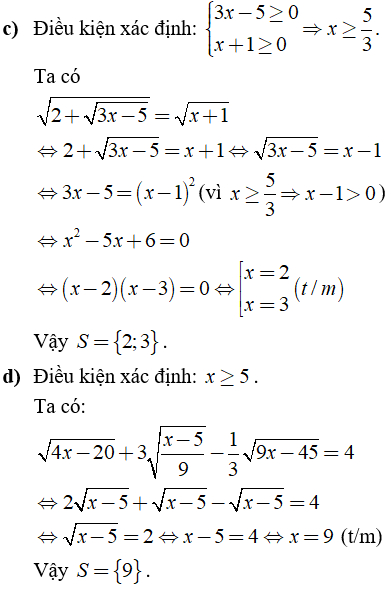
Câu 4: Tính giá trị của biểu thức x2 + y2 biết rằng ![]()
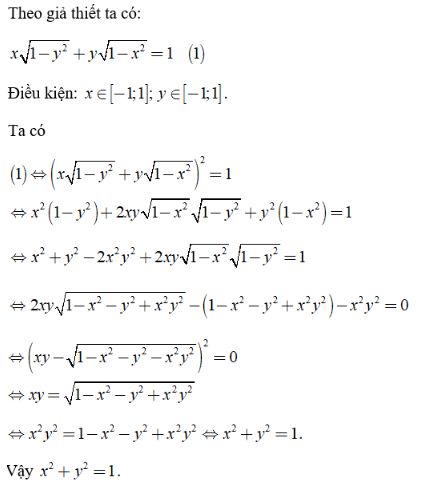
...................................
Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 9: Liên hệ giữa phép nhân và phép khai phương. Với bài Liên hệ giữa phép nhân và phép khai phương trên đây các bạn học sinh cần nắm vững kiến thức về định nghĩa về căn thức bậc hai của một tích, căn thức bậc hai của một thương,....
Để có kết quả cao hơn trong h ọc tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 9, Giải bài tập Toán lớp 9 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc.








