Chuyên đề Toán 9: Đường tròn ngoại tiếp tam giác Đường tròn nội tiếp tam giác
Đường tròn ngoại tiếp tam giác Đường tròn nội tiếp tam giác
Đường tròn ngoại tiếp và đường tròn nội tiếp tam giác là hai kiến thức quan trọng trong chương trình Toán 9, thuộc phần hình học lớp 9 nâng cao. Đây là chuyên đề thường gặp trong các đề kiểm tra và đề thi vào lớp 10. Trong bài viết này, chúng ta sẽ cùng tìm hiểu khái niệm, tính chất, cách dựng đường tròn ngoại tiếp và nội tiếp của một tam giác, cùng các dạng bài tập thường gặp có lời giải chi tiết. Với cách trình bày logic, dễ hiểu, tài liệu này sẽ giúp học sinh nắm vững kiến thức và vận dụng thành thạo vào giải toán.
A. Đường tròn ngoại tiếp một tam giác
Đường tròn đi qua ba đỉnh của một tam giác gọi là đường tròn ngoại tiếp tam giác. Khi đó tam giác gọi là tam giác nội tiếp đường tròn.
- Tâm đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của tam giác.
- Bán kính là khoảng cách từ giao điểm của ba đường trung trực đến một điểm bất kì của tam giác.
B. Đường tròn nội tiếp một tam giác
Đường tròn tiếp xúc với ba cạnh của tam giác được gọi là đường tròn nội tiếp tam giác. Khi đó tam giác được gọi là tam giác ngoại tiếp đường tròn.
- Tâm đường tròn nội tiếp tam giác là giao điểm của ba đường phân giác trong.
- Bán kính bằng khoảng cách từ giao điểm đó đến một cạnh bất kì của tam giác.
B. Các dạng bài tập về đường tròn nội tiếp – ngoại tiếp lớp 9
Dạng I. Tính toán
Bài toán 1. Cho tam giác 
\(ABC\) vuông tại \(A\) có \(AB = 3\ cm,\ \ AC = 4\ cm.\) Xác định tâm và bán kính của đường tròn ngoại tiếp tam giác \(ABC.\)
Lời giải
Gọi \(O\) là trung điểm của cạnh huyền \(BC\) của tam giác vuông \(ABC\).
Ta có \(AO\) là trung tuyến của tam giác vuông \(ABC\) nên \(OA = \frac{1}{2}BC = OB = OC.\)
Vậy đường tròn ngoại tiếp tam giác \(ABC\) là đường tròn có tâm \(O\) là trung điểm của \(BC\).
Vì tam giác \(ABC\) vuông tại \(A\) nên theo định lí Pythagore, ta có:
\(\begin{matrix}
BC^{2} = AB^{2} + AC^{2} = 3^{2} + 4^{2} = 25 \\
\Rightarrow BC = \sqrt{25} = 5\ (cm) \\
\end{matrix}\)
Vậy bán kính của đường tròn là \(5:2 = 2,5\
(cm)\)
Bài toán 2. Cho tam giác đều \(ABC\) nội tiếp đường tròn \((O)\). Biết rằng đường tròn \((O)\) có bán kính bằng \(3\ cm.\) Tính diện tích tam giác \(ABC.\)
Lời giải
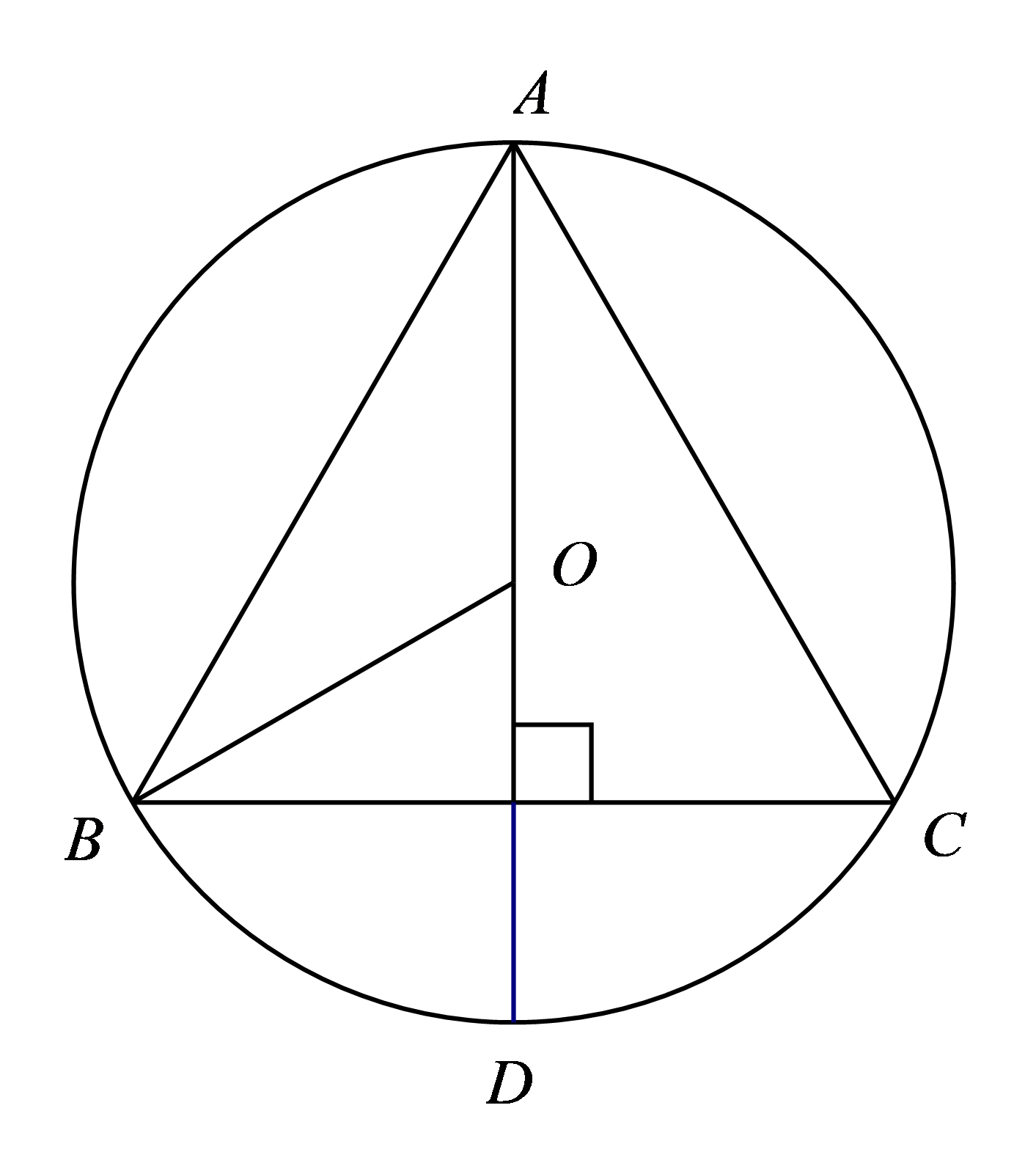
Kẻ đường cao \(AH\) vì tam giác \(ABC\) đều (gt) nên đường cao \(AH\) đồng thời là đường phân giác của góc \(BAC\), ta có: \(\widehat{BAH} = \widehat{CAH} =
\frac{\widehat{BAC}}{2} = \frac{60{^\circ}}{2} =
30{^\circ}.\)
Kéo dài \(AH\) cắt đường tròn \((O)\) tại \(D\). Khi đó \(\widehat{BOD}\) và \(\widehat{BAD}\) lần lượt là góc ở tâm và góc nội tiếp cùng chắn \(\widehat{BD}\) ) \(\Rightarrow \widehat{BOD} =
2.\widehat{BAD} = 2.30{^\circ} = 60{^\circ}.\)
Tam giác \(BHO\) vuông tại \(H\) có cạnh huyền \(OB = 3\ cm\) (gt) và \(\widehat{BOD} = 60{^\circ}.\)
Theo định lí về hệ thức lượng trong tam giác vuông, ta có: \(BH = OB.sinBOH = 3.sin60{^\circ} =
\frac{3\sqrt{3}}{2}\ \ (cm)\)
Vì \(\Delta ABC\) đều nên đường cao \(AH\) đồng thời là trung tuyến hay \(H\) là trung điểm của \(BC.\)
\(\Rightarrow BC = 2BH =
2.\frac{3\sqrt{3}}{2} = 3\sqrt{3}\ \ (cm)\)
Xét tam giác \(AHB\) vuông tại \(H\) có cạnh huyền: \(AB = BC = 3\sqrt{3}\ (cm)\) và \(\widehat{BAH} = 30{^\circ}(cmt)\)
Theo định lí về hệ thức lượng trong tam giác vuông, ta có:
\(AH = AB.cosBAH = 3\sqrt{3}.cos30{^\circ}
= \frac{9}{2}\ (cm)\)
Gọi \(S_{ABC}\) là diện tích tam giác đều, ta có: \(S_{ABC} = \frac{1}{2}AH.BC
= \frac{1}{2}.\frac{9}{2}.3\sqrt{3} = \frac{27\sqrt{3}}{4}\
(cm^{2}).\)
Bài toán 3. Cho tam giác \(ABC\) nội tiếp đường tròn \((O).\) Biết rằng \(\widehat{BOC} = 120{^\circ}\) và \(\widehat{OCA} = 20{^\circ}\). Tính số đo các góc của tam giác \(ABC.\)
Lời giải
Xét đường tròn \((O),\) ta có \(\widehat{BAC}\) và \(\widehat{BOC}\) và góc ở tâm cùng chắn \(\widehat{BC}\). nên \(\widehat{BAC} = \frac{1}{2}\widehat{BOC} =
\frac{1}{2}.120{^\circ} = 60{^\circ}.\)
Tam giác \(\widehat{BOC}\) cân tại \(O\) có góc ở đỉnh \(\widehat{BOC} = 120{^\circ}\) (GT)
\(\Rightarrow \widehat{OBC} = \widehat{OCB}
= \frac{180{^\circ} - \widehat{BOC}}{2} = \frac{180{^\circ} -
120{^\circ}}{2} = 30{^\circ}.\)
Do đó, \(\widehat{BCA} = \widehat{OCB} +
\widehat{OCA} = 30{^\circ} + 20{^\circ} = 50{^\circ}.\)
Xét tam giác \(ABC,\) ta có:
\(\widehat{ABC} = 180{^\circ} - \left(
\widehat{BAC} + \widehat{BCA} \right)\)
\(\ \ \ \ \ \ \ \ \ \ \ \ = 180{^\circ} -
(60{^\circ} + 50{^\circ}) = 70{^\circ}\)
Vậy số đo các góc của tam giác \(ABC\) là: \(\widehat{BAC} = 60{^\circ};\ \widehat{ABC} =
70{^\circ};\ \widehat{BCA} = 50{^\circ}.\)
Dạng II. Bài toán thực tế
Bài toán 1. Một mảnh vườn có dạng hình tam giác đều \(ABC\) cạnh \(12\
m\). Người ta muốn trồng hoa ở phần đất bên trong đường tròn nội tiếp tam giác \(ABC\). Tính diện tích phân đất trồng hoa đó.
Lời giải
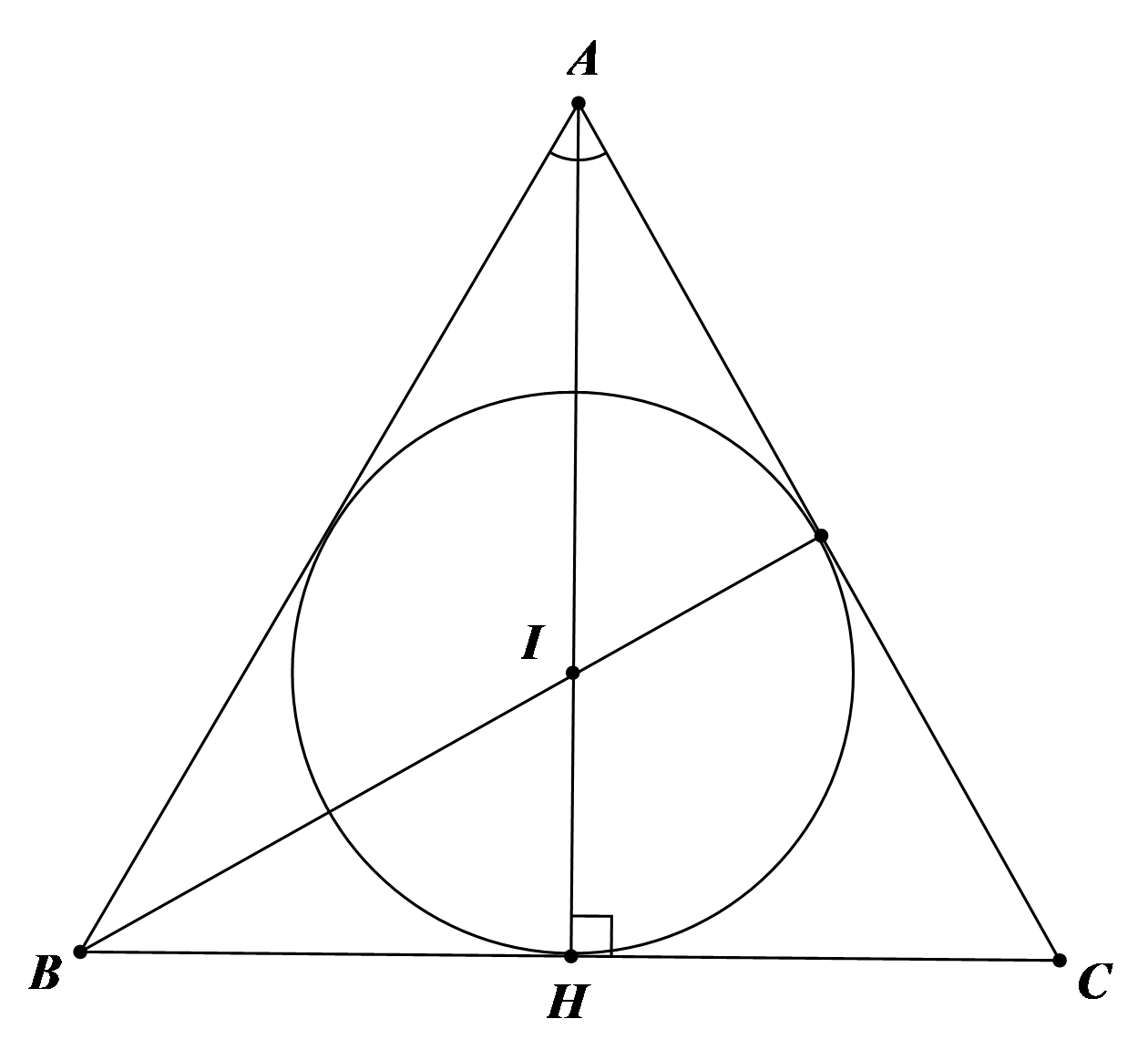
Gọi \(I\) là tâm đường trò nội tiếp tam giác đều \(ABC\).
Kẻ đường cao \(AH\), khi đó tâm \(I\) của đường tròn nội tiếp (giao điểm của ba đường phân giác cũng là trọng tâm).
Ta có \(AH\) là đường trung tuyến suy ra \(H\) là trung điểm của \(BC\) hay \(BH =
CH = \frac{BC}{2} = \frac{12}{2} = 6\ (m)\).
Xét tam giác \(BHI\) vuông tại \(H\). Có \(BH = 6\
m\) và \(\widehat{IBH} =
30{^\circ}\).
Theo định lý về hệ thức lượng trong tam giác vuông, ta có:
\(IH = BH.tan\widehat{IBH} =
6.tan30{^\circ} = 2\sqrt{3}\ (m)\).
Vậy bán kính của phần đất trồng hoa là \(2\sqrt{3}\ (m)\).
Do đó diện tích phần đất trồng hoa là \(S =
\pi.\left( 2\sqrt{3} \right)^{2} = 12\pi\ \ \left( m^{2}
\right)\).
Bài toán 2. Ba vị trí \(A\) \(B\), \(C\) ở một công viên là ba đỉnh của một tam giác đều cạnh \(15\ m\). Người ta cần chọn vị trí \(O\) cách đều ba vị trí \(A\), \(B\), \(C\) để làm một cột đèn. Tính khoảng cách từ vị trí \(O\) đến mỗi vị trí \(A\), \(B\), \(C\).
Lời giải
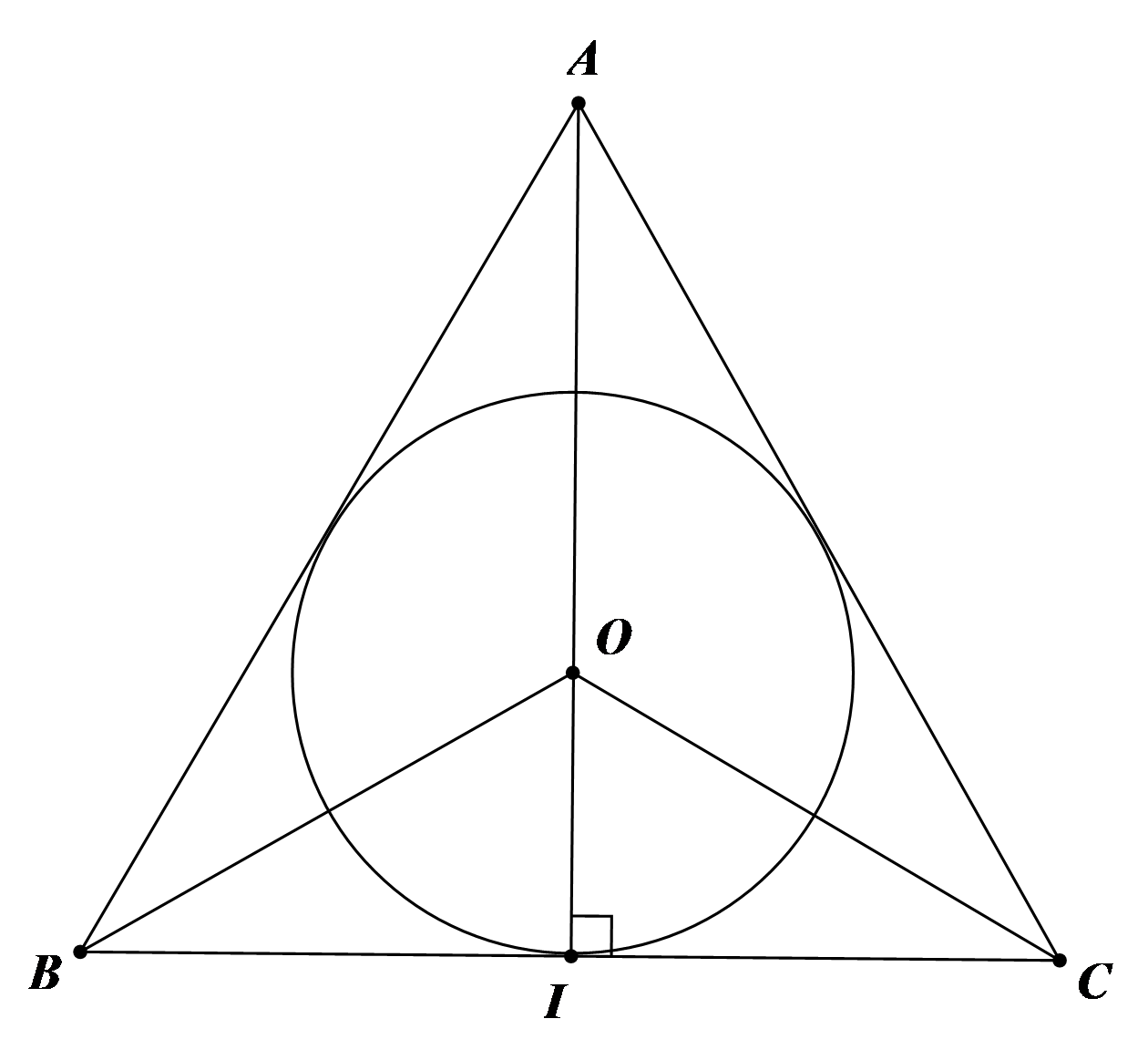
Gọi \(O\) là vị trí cách đều ba vị trí \(A\), \(B\), \(C\) nên \(O\) là tâm đường tròn ngoại tiếp tam giác \(ABC\) (giao điểm của ba đường trung trực).
Do \(\Delta ABC\) đều (gt) nên \(O\) đồng thời là trực tâm và trọng tâm của tam giác hay \(AH\) là đường cao của tam giác \(ABC\) đều cạnh \(15\ m\).
Suy ra \(AH = \frac{15\sqrt{3}}{2}\
(m)\) vì \(AH\) đồng thời là trung tuyến của \(\Delta ABC\) có trọng tâm \(O\) suy ra \(OA = \frac{2}{3}AH = \frac{2}{3} \cdot
\frac{15\sqrt{3}}{2} = 5\sqrt{3}\ (m)\).
Vậy khoảng cách từ vị trí \(O\) đến mỗi vị trí \(A\), \(B\), \(C\) là \(5\sqrt{3}\ (m)\).
Dạng III. Chứng minh
Bài toán 1. Cho tam giác \(ABC\) nội tiếp đường tròn \((O)\). Gọi \(H\) là trực tâm tâm tam giác \(ABC\). Chứng minh rằng \(\widehat{BAH} = \widehat{OAC}\).
Lời giải
Gọi \(OI\) là đường cao của tam giác \(AOC\) cân tại \(O\), ta có \(OI\) đồng thời là đường phân giác của góc \(\widehat{AOC}\) hay \(\widehat{AOI} = \widehat{COI} =
\frac{1}{2}\widehat{AOC}\).
Xét đường tròn \((O)\) ta có \(\widehat{ABC}\) và \(\widehat{AOC}\) lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung \(AC\) nên \(\widehat{ABC} =
\frac{\widehat{AOC}}{2}\) hay \(\widehat{ABC} = \widehat{AOI}\).
Hai tam giác \(APB\) và \(AIO\) đều vuông tại \(P\) và \(I\) mà \(\widehat{ABP} = \widehat{AOI}\) (chứng minh trên)
Nên suy ra \(\widehat{BAH} =
\widehat{OAC}\) (cùng phụ với hai góc bằng nhau).
Bài toán 2. Cho tam giác nhọn \(ABC\) \((AB <
AC)\) nội tiếp đường tròn \((O)\) đường kính \(AD = 2R\). Gọi \(M\) là trung điểm của cạnh \(BC\) và \(H\) là trực tâm của tam giác \(ABC\). Chứng minh:
a) \(DB\bot AB\) và \(CD\bot AC\).
b) Tứ giác \(BHCD\) là hình bình hành.
c) \(AC^2 + BH^2 = 4R^2\).
d) Ba điểm \(H\), \(M\), \(D\) thẳng hàng và \(AH = 2OM\).
Lời giải
a) Xét tam giác \(ABD\), ta có: \(OB = OA = OD( = R)\) hay \(OB = AD\)
Chứng tỏ \(\Delta ABD\) vuông tại \(B\)
Hay \(DB\bot AB\) (đpcm)
Chứng minh tương tự ta có \(CD\bot
AC\).
b) Ta có \(BH// DC\) (cùng vuông góc với \(AC\) )
Tương tự \(CH\ //\ BD\) ( ùng vuông góc với \(AB\) )
Tứ giác \(BHCD\) là hình bình hành (Các cạnh đối song song)
c) Ta có tam giác \(ACD\) vuông tại \(C\) (chứng minh trên)
\(AC^{2} + DC^{2} = AD^{2}\) (định lí pythagore)
Mà \(DC = BH\) (cmt) \(AC^{2} + BH^{2} = AD^{2} = (2R)^{2} =4R^{2}\).
d) Ta có \(M\) là trung điểm của \(BC\) (gt) mà tứ giác \(BHCD\) là hình bình hành (cmt) nên đường chéo thứ hai \(HD\) phải qua trung điểm \(M\) hay ba điểm \(H,M,D\) thẳng hàng.
* Xét tam giác \(AHD\) có \(O\) là trung điểm của \(AD\) (gt)
\(M\) là trung điểm của \(HD\) (cmt) nên \(OM\) là đường trung bình của tam giác \(AHD\) \(\Rightarrow AH=2.OM\)
D. Bài tập đường tròn nội tiếp, ngoại tiếp có lời giải lớp 9
Bài toán 1. Xác định tâm và bán kính của đường tròn ngoại tiếp tam giác đều \(ABC\) có cạnh bằng \(a.\)
Bài toán 2. Tính bán kính đường tròn ngoại tiếp tam giác \(ABC\) vuông tại \(A\), biết \(AB =
5\ cm,\ \ AC = 12\ cm\)
Bài toán 3. Cho đường tròn \((O)\) ngoại tiếp tam giác \(ABC\). Tính bán kính của \((O)\), biết rằng \(\Delta ABC\) vuông cân tại \(A\) và có cạnh bằng \(2\sqrt{2}\ \ cm.\)
Bài toán 4: Cho tam giác \(ABC\) vuông tại \(B\) có \(\widehat{C} = 60{^\circ},\ BC = 3\ cm\) và \(O\) là trung điểm \(AC.\) Xác định tâm, bán kính và vẽ đường tròn ngoại tiếp của
a) \(\Delta ABC\); b) \(\Delta BCD.\)
Bài toán 5. Cho tam giác đều \(ABC\) có cạnh bằng \(3\ cm\) và nội tiếp đường tròn \((O)\) như hình vẽ.
a) Tính bán kính \(R\) của đường tròn \((O).\)
b) Tính diện tích hình viên phân giới hạn bởi dây cung \(BC\) và cung nhỏ \(BC.\)
Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!
--------------------------------------------------
Trên đây là nội dung chuyên đề đường tròn ngoại tiếp và đường tròn nội tiếp tam giác Toán 9, bao gồm đầy đủ lý thuyết trọng tâm và bài tập vận dụng có lời giải chi tiết. Hy vọng tài liệu này sẽ giúp bạn hiểu sâu kiến thức, rèn luyện kỹ năng giải bài toán hình học và đạt kết quả tốt trong các kỳ thi. Đừng quên kết hợp với các chuyên đề liên quan như góc nội tiếp, tính chất tam giác, hay định lý đường trung trực để học hình học lớp 9 một cách toàn diện. Chúc bạn học tốt!
