Tứ giác nội tiếp đường tròn lớp 9

Trong chương trình Toán lớp 9, Tứ giác nội tiếp đường tròn là một chuyên đề quan trọng, thường xuyên xuất hiện trong các đề thi học kỳ và kỳ thi vào lớp 10. Bài viết này sẽ giúp bạn hệ thống hóa lý thuyết, dấu hiệu nhận biết, tính chất và phương pháp giải bài tập liên quan đến tứ giác nội tiếp một cách dễ hiểu, đầy đủ và trực quan nhất. Hãy cùng khám phá những kiến thức trọng tâm và mẹo làm bài nhanh gọn nhé!

A. Tổng hợp kiến thức tứ giác nội tiếp lớp 9

1. Tứ giác nội tiếp là gì?

Tứ giác nội tiếp là tứ giác có bốn đỉnh nằm trên đường tròn đó.

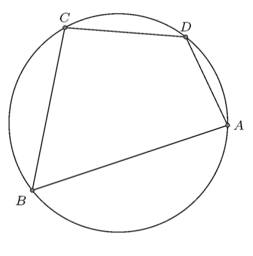
Trong hình vẽ, tứ giác \(ABCD\) nội tiếp đường tròn \((O)\) và đường tròn \((O)\) gọi là ngoại tiếp tứ giác.

2. Định lí

Tứ giác nội tiếp đường tròn khi và chỉ khi tổng số đo của hai góc đối bằng \(180^{0}\).

3. Dấu hiệu nhận biết tứ giác nội tiếp

• Tổng của hai góc đối bằng \(180^{0}\).
• Tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh không kề với nó.
• Tứ giác có bốn đỉnh cách đều một điểm \(O\) cố định.
• Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh nối hai đỉnh còn lại với góc bằng nhau.

Chú ý:

Trong các hình tứ giác đã học thì hình vuông, hình chữ nhật, hình thang cân là các tứ giác nội tiếp được trong đường tròn.

B. Các dạng bài tập tứ giác nội tiếp và phương pháp giải

Dạng 1: Tính số đo các góc và chứng minh tứ giác nội tiếp

Phương pháp giải: Sử dụng định lý về điều kiện của tứ giác nội tiếp.

Ví dụ. Cho tứ giác \(ABCD\) nội tiếp đường tròn tâm \(M\). Biết \(\widehat{DAB} = 80^{0}\), \(\widehat{DAM} = 30^{0}\) và \(\widehat{BMC} = 70^{0}\). Tính số đo các góc \(\widehat{MAB}\), \(\widehat{BCM}\) và \(\widehat{BCD}\).

Hướng dẫn giải

Hình vẽ minh họa

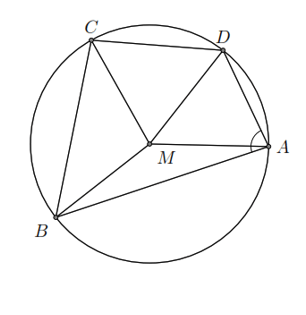
Ta có \(\widehat{DAB} = \widehat{DAM} + \widehat{MAB}\) \(\Rightarrow \widehat{MAB} = \widehat{DAB} - \widehat{DAM} = 80^{0} - 30^{0} = 50^{0}\).

Do tam giác \(CBM\) cân tại \(M\) nên \(\widehat{BCM} = \frac{180^{{^\circ}} - \widehat{BMC}}{2} = 55^{{^\circ}}\).

Do tứ giác \(ABCD\) nội tiếp nên \(\widehat{BCD} = 180^{{^\circ}} - \widehat{DAB} = 100^{{^\circ}}\).

Ví dụ. Cho tam giác \(ABC\) nhọn các đường cao \(BM,CN\) cắt nhau tại \(H\). Chứng minh rằng \(AMHN\) và \(BNMC\) là các tứ giác nội tiếp.

Hướng dẫn giải

Hình vẽ minh họa

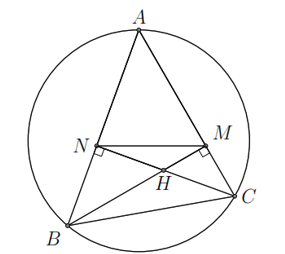
Ta có \(\widehat{AMB} = \widehat{ANC} = 90^{{^\circ}}\) suy ra \(\widehat{AMH} + \widehat{ANH} = 180^{0}\) hay tứ giác \(AMHN\) nội tiếp.

Và \(BNMC\) có \(\widehat{AMB} = \widehat{ANC} = 90^{{^\circ}}\) nên nội tiếp.

Ví dụ. Cho tứ giác \(ABCD\) nội tiếp đường tròn tâm \(O\), \(AB\) và \(CD\) cắt nhau tại \(E\), \(BC\) và \(AD\) cắt nhau tại \(F\). Cho biết \(\widehat{BEC} = 40^{{^\circ}},\widehat{CFD} = 20^{{^\circ}}\). Tính số đo các góc của tứ giác.

Hướng dẫn giải

Hình vẽ minh họa

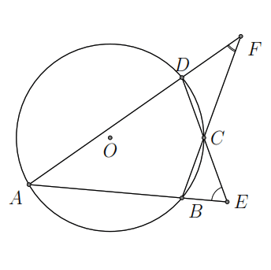
Ta có \(\widehat{BEC} = \frac{1}{2}\left( sd\widehat{AD} - sd\widehat{BC} \right)\), \(\widehat{DFC} = \frac{1}{2}\left( sd\widehat{AB} - sd\widehat{DC} \right)\).

Suy ra \(\frac{1}{2}\left( sd\widehat{AD} + sd\widehat{AB} \right) - \frac{1}{2}\left( sd\widehat{BC} + sd\widehat{DC} \right) = 60^{0}\).

Hay \(\frac{1}{2}sd\widehat{BAD} - \frac{1}{2}sd\widehat{BCD} = 60^{0} \Rightarrow \widehat{DCB} - \widehat{DAB} = 60^{0}\)

Mà tứ giác \(ABCD\) nội tiếp nên \(\widehat{DCB} + \widehat{DAB} = 180^{0}\).

Do đó \(\widehat{DCB} = 120^{{^\circ}},\widehat{DAB} = 60^{{^\circ}}\).

Tương tự như trên ta suy ra \(\widehat{ABC} = 80^{0},\widehat{ADC} = 100^{0}\).

Ví dụ. Trên đường tròn \((O)\) có một cung \(AB\), \(S\) là điểm chính giữa của cung đó. Trên dây \(AB\) lấy hai điểm \(E,H\). Các đường thẳng \(SE,SH\) cắt đường tròn theo thứ tự tại \(C,D\). Chứng minh rằng:

a) \(\widehat{SHA} = \widehat{SCD}\).                                     b) Tứ giác \(EHCD\) nội tiếp.

Hướng dẫn giải

Hình vẽ minh họa:

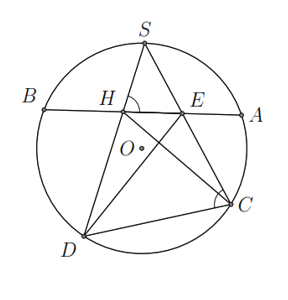
a) Ta có \(\widehat{SCD} = \frac{1}{2}sd\widehat{SD}\)

và \(\widehat{SHA} = \frac{1}{2}\left( sd\widehat{SA} + sd\widehat{BD} \right) = \frac{1}{2}\left( sd\widehat{SB} + sd\widehat{BD} \right) = \frac{1}{2}sd\widehat{SD}\) do \(SA = SB\).

Do đó \(\widehat{SHA} = \widehat{SCD}\).

Theo câu trên ta có \(\widehat{SHA} = \widehat{SCD}\) mà \(\widehat{SHA} + \widehat{DHE} = 180^{{^\circ}}\) nên \(\widehat{ECD} + \widehat{DHE} = 180^{{^\circ}}\). Suy ra tứ giác \(EHCD\) nội tiếp.

Dạng 2: Khai thác tính chất của tứ giác nội tiếp

Phương pháp:

Sử dụng các tính chất về tổng hai góc đối trong tứ giác nội tiếp hay các góc chắn một cung…

Ví dụ. Cho tam giác \(ABC\) nhọn nội tiếp đường tròn \((O)\). Các đường cao \(AD,BE,CF\) cắt nhau tại \(H\) và cắt đường tròn \((O)\) lần lượt tại \(M,N,P\). Chứng minh rằng

a) Tứ giác \(CEHD\) nội tiếp.

b) Bốn điểm \(B,C,E,F\) cùng thuộc một đường tròn.

c) \(AE \cdot AC = AH \cdot AD\) và \(AD \cdot BC = BE \cdot AC\).

d) \(H,M\) đối xứng nhau qua \(BC\).

Hướng dẫn giải

Hình vẽ minh họa

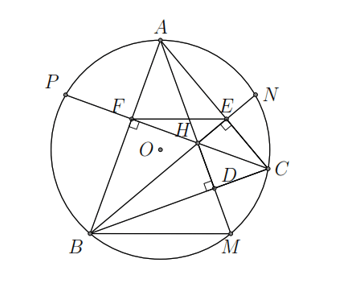
a) Ta có \(\widehat{CEH} = \widehat{HDC} = 90^{{^\circ}}\) suy ra tứ giác \(CEHD\) có tổng hai góc đối bằng \(180^{{^\circ}}\) nên nội tiếp.

Ta có \(\widehat{CEB} = \widehat{CFB} = 90^{{^\circ}}\) suy ra tứ giác \(BCEF\) nội tiếp.

Do hai tam giác vuông \(AEB\) và \(AFC\) đồng dạng (g-g) nên \(AE \cdot AC = AH \cdot AD\).

Ta có \(AD \cdot BC = BE \cdot AC = \frac{1}{2}S_{ABC}\).

Ta có \(\widehat{ADB} = \widehat{AEB} = 90^{{^\circ}}\) nên tứ giác \(ABDE\) nội tiếp.

Do đó \(\widehat{CAM} = \widehat{NBC}\) (cùng chắn cung \(ED\)) nên \(\widehat{CBM} = \widehat{CAM} = \widehat{NBC}\) . Suy ra tam giác \(HBM\) cân tại \(B\) hay \(H,M\) đối xứng nhau qua \(BC\).

Ví dụ. Cho tam giác \(ABC\) cân tại \(A\) các đường cao \(AD,BE\) cắt nhau tại \(H\). Gọi \(I\) là tâm đường tròn ngoại tiếp tam giác \(AHE\). Chứng minh rằng

a) Tứ giác \(CEHD\) nội tiếp.

b) Bốn điểm \(A,E,B,D\) cùng thuộc một đường tròn.

c) \(ED = \frac{1}{2}BC\).

d) \(DE\) là tiếp tuyến của đường tròn \((I)\).

Hướng dẫn giải

Hình vẽ minh họa

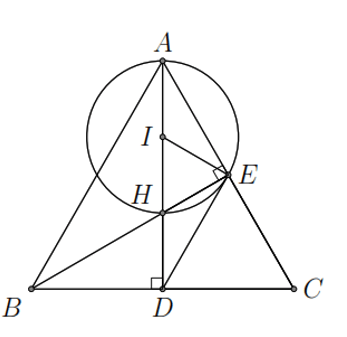
a) Ta có \(\widehat{CEH} = \widehat{HDC} = 90^{{^\circ}}\) suy ra tứ giác \(CEHD\) có \(\widehat{CEH} + \widehat{HDC} = 180^{{^\circ}}\) nên nội tiếp.

Ta có \(\widehat{BEA} = \widehat{ADB} = 90^{{^\circ}}\) suy ra tứ giác \(AEDB\) nội tiếp.

Ta có tam giác \(BEC\) vuông tại \(E\) và \(D\) là trung điểm \(BC\) suy ra \(ED = \frac{1}{2}BC\).

Ta có \(\widehat{EIH} = 2\widehat{EIH} = \widehat{CAB}\). Do tứ giác \(ABDE\) nội tiếp suy ra \(\widehat{ABE} = \widehat{ADE}\). Mà \(\widehat{CAB} + \widehat{ABE} = 90^{{^\circ}} \Rightarrow \widehat{EIH} + \widehat{ADE} = 90^{{^\circ}}\). Suy ra \(IE\bot DE\) hay \(DE\) là tiếp tuyến của đường tròn \((I)\).

C. Bài tập tứ giác nội tiếp có lời giải

Bài 1. Cho tam giác \(ABC\) nội tiếp đường tròn \((O)\). Gọi \(M\) là điểm chính giữa cung nhỏ \(BC\) và \(N\) là một điểm thuộc cung nhỏ \(AB\). \(AM\), \(MN\) cắt \(BC\) lần lượt tại \(D,E\). Chứng minh rằng tứ giác \(ADEN\) nội tiếp.

Bài 2. Cho đường tròn tâm \(O\) đường kính \(AB = 2R\) và điểm \(C\) thuộc đường tròn đó (\(C\) khác \(A,B\)). Lấy điểm \(D\) thuộc dây \(BC\) (\(D\) khác \(B,C\)). Tia \(AD\) cắt cung nhỏ \(BC\) tại điểm \(E\), tia \(AC\) cắt \(BE\) tại \(F\). Chứng minh

a) \(FCDE\) nội tiếp.                  b) \(\widehat{CFD} = \widehat{OCB}\).                    c) \(DA \cdot DE = DB \cdot DC\).

Bài 3. Cho tam giác \(ABC\) nhọn nội tiếp đường tròn \((O)\). Các đường cao \(BD,CE\) cắt nhau tại \(H\). Chứng minh

a) Các tứ giác \(ADHE\) và \(BCDE\) nội tiếp.

b) \(AE \cdot AB = AD \cdot AC\).                                 c) \(OA\bot DE\).

Bài 4. Cho đường tròn \((O)\) và điểm \(A\) nằm ngoài đường tròn. Từ \(A\) vẽ hai tiếp tuyến \(AB,AC\) và cát tuyến \(AMN\) với đường tròn (\(AM < AN\)). Gọi \(I\) là giao điểm thứ hai của đường thẳng \(CE\) với đường tròn (\(E\) là trung điểm của \(MN\)). Chứng minh

a) Bốn điểm \(A,O,E,C\) cùng thuộc một đường tròn.

b) \(\widehat{AOC} = \widehat{BIC}\).

c) \(BI\) song song với \(MN\).

Bài 5. Cho đường tròn \((O,R)\) và điểm \(M\) nằm ngoài đường tròn. Từ \(M\) vẽ hai tiếp tuyến \(MA,MB\) và cát tuyến \(MNP\) với đường tròn. Gọi \(K\) là trung điểm \(NP\), kẻ \(AC\bot MB,\) \(BD\bot MA\). Gọi \(H\) là giao điểm của \(AC\) và \(BD\), \(I\) là giao điểm của \(OM\) và \(AB\). Chứng minh

a) Bốn điểm \(A,O,B,M\) cùng thuộc một đường tròn.

b) Năm điểm \(O,K,A,M,B\) cùng thuộc một đường tròn.

c) \(OI \cdot OM = R^{2}\).

d) \(AOHB\) là hình thoi.

e) \(O,H,M\) thẳng hàng.

Toàn bộ nội dung đã sẵn sàng! Nhấn Tải về để tải đầy đủ tài liệu.

---------------------------------------------

Trên đây là toàn bộ kiến thức cốt lõi và bài tập điển hình về tứ giác nội tiếp đường tròn lớp 9. Hy vọng tài liệu này sẽ giúp bạn học tập hiệu quả, củng cố kỹ năng giải toán và tự tin chinh phục các kỳ thi quan trọng. Đừng quên luyện tập thường xuyên và theo dõi các chuyên đề Toán học khác để đạt kết quả tốt nhất nhé!