VnDoc.com Lớp 9 Giải SBT Toán 9

Giải SBT Toán 9 bài 3: Liên hệ giữa phép nhân và phép khai phương

Giải Toán 9 SBT bài 3
5 2.197
Bài viết đã được lưu

Giải SBT Toán 9 bài 3: Liên hệ giữa phép nhân và phép khai phương được VnDoc sưu tầm và đăng tải theo sát SBT Toán lớp 9. Hy vọng tài liệu này sẽ giúp ích cho các bạn trả lời các câu hỏi trong sách bài tập Toán 9. Chúc các bạn học tốt, mời các bạn tham khảo

Giải sách bài tập Toán 9 bài 3

Ngoài ra, VnDoc.com đã thành lập group chia sẻ tài liệu học tập THCS miễn phí trên Facebook: Tài liệu học tập lớp 9. Mời các bạn học sinh tham gia nhóm, để có thể nhận được những tài liệu mới nhất.

Giải Toán 9: SBT Bài 23 trang 9 Sách bài tập Toán 9 Tập 1

Áp dụng quy tắc nhân các căn thức bậc hai, hãy tính:

a. \sqrt{40}
b. \sqrt{5}
c. \sqrt{52} \cdot \sqrt{13}
d. \sqrt{2.162}

Lời giải:

a. \sqrt{10} \cdot \sqrt{40}=\sqrt{10.40}=\sqrt{400}=20
b. \sqrt{5} \cdot \sqrt{45}=\sqrt{5.45}=\sqrt{225}=15
c. \sqrt{52} \cdot \sqrt{13}=\sqrt{4.13 \cdot 13}=\sqrt{(2.13)^{2}}=2.13=26
d. \sqrt{2.162}=\sqrt{2.2 .81}=\sqrt{(2.9)^{2}}=2.9=18

Giải Toán 9: Bài 24 (trang 9 Sách bài tập Toán 9 Tập 1

Áp dụng quy tắc khai phương một tích, hãy tính:

a. \sqrt{45.80}
b. \sqrt{75.48}
c. \sqrt{90.6,4}
d. \sqrt{2,5.14,4}

Lời giải:

a. \sqrt{45.80}=\sqrt{9.5 .5 .16}=\sqrt{9} \cdot \sqrt{5^{2}} \cdot \sqrt{16}=3.5 .4=60
b. \sqrt{75.48}=\sqrt{25.3 .3 .16}=\sqrt{25} \cdot \sqrt{3^{2}} \cdot \sqrt{16}=5.3 .4=60
c. \sqrt{90.6,4}=\sqrt{9.64}=\sqrt{9} \cdot \sqrt{64}=3.8=24
d. \sqrt{2,5.14,4}=\sqrt{25.1,44}=\sqrt{25} \cdot \sqrt{1,44}=5.1,2=6

Giải Toán 9: Bài 25 trang 9 Sách bài tập Toán 9 Tập 1

Rút gọn rồi tính:

a.\ \sqrt{6,8^2-3,2^2}
b. \sqrt{21,8^{2}-18,2^{2}}
c. \sqrt{117,5^{2}-26,5^{2}-1440}
d. \sqrt{146,5^{2}-109,5^{2}+27.256}

Lời giải:

a. \sqrt{6,8^{2}-3,2^{2}}=\sqrt{(6,8+3,2)(6,8-3,2)}=\sqrt{10.3,6}=\sqrt{36}=6
b. \sqrt{21,8^{2}-18,2^{2}}=\sqrt{(21,8+18,2)(21,8-18,2)}=\sqrt{40.3,6}
=\sqrt{4.36}=\sqrt{4} \cdot \sqrt{36}=2.6=12
c. \sqrt{117,5^{2}-26,5^{2}-1440}=\sqrt{(117,5+26,5)(117,5-26,5)-1440}
=\sqrt{144.91-1440}=\sqrt{144 .(91-10)}
=\sqrt{144.81}=\sqrt{144} \cdot \sqrt{81}=12.9=108
d. \sqrt{146,5^{2}-109,5^{2}+27.256}
=\sqrt{(146,5+109,5)(146,5-109,5)+27.256}
=\sqrt{256.37+27.256}=\sqrt{256 .(37+27)}=\sqrt{256} \cdot \sqrt{64}=16.8=128

Giải Toán 9: Bài 26 trang 9 Sách bài tập Toán 9 Tập 1

Chứng minh:

a. \sqrt{9-\sqrt{17}} \cdot \sqrt{9+\sqrt{17}}=8
b. 2 \sqrt{2}(\sqrt{3}-2)+(1+2 \sqrt{2})^{2}-2 \sqrt{6}=9

Lời giải:

\begin{aligned} &\text { a. Ta có: } \sqrt{9-\sqrt{17}} \cdot \sqrt{9+\sqrt{17}}=\sqrt{(9-\sqrt{17})(9+\sqrt{17})}\\ &=\sqrt{81-17}=\sqrt{64}=8 \end{aligned}

Vế trái bằng vế phải nên đẳng thức được chứng minh.

b. Ta có: 2\sqrt{2}(\sqrt{3}-2)+(1+2\sqrt{2})^2-2\sqrt{6}

=2\sqrt{6}-4\sqrt{2}+1+4\sqrt{2}+8-2\sqrt{6}=1+8=9

Giải Toán 9: Bài 27 trang 9 Sách bài tập Toán 9 Tập 1

Rút gọn:

a. \frac{\sqrt{6}+\sqrt{14}}{2 \sqrt{3}+\sqrt{28}}
b. \frac{\sqrt{2}+\sqrt{3}+\sqrt{6}+\sqrt{8}+\sqrt{16}}{\sqrt{2}+\sqrt{3}+\sqrt{4}}

Lời giải:

a. \frac{\sqrt{6}+\sqrt{14}}{2 \sqrt{3}+\sqrt{28}}=\frac{\sqrt{2.3}+\sqrt{2.7}}{2 \sqrt{3}+\sqrt{4} \cdot \sqrt{7}}=\frac{\sqrt{2}(\sqrt{3}+\sqrt{7})}{2(\sqrt{3}+\sqrt{7})}=\frac{\sqrt{2}}{2}
b. \frac{\sqrt{2}+\sqrt{3}+\sqrt{6}+\sqrt{8}+\sqrt{16}}{\sqrt{2}+\sqrt{3}+\sqrt{4}}=\frac{\sqrt{2}+\sqrt{3}+\sqrt{6}+\sqrt{8}+4}{\sqrt{2}+\sqrt{3}+\sqrt{4}}
=\frac{\sqrt{2}+\sqrt{3}+\sqrt{4}+\sqrt{4}+\sqrt{6}+\sqrt{8}}{\sqrt{2}+\sqrt{3}+\sqrt{4}}
=\frac{(\sqrt{2}+\sqrt{3}+\sqrt{4})+\sqrt{2}(\sqrt{2}+\sqrt{3}+\sqrt{4})}{\sqrt{2}+\sqrt{3}+\sqrt{4}}
=\frac{(\sqrt{2}+\sqrt{3}+\sqrt{4})(1+\sqrt{2})}{\sqrt{2}+\sqrt{3}+\sqrt{4}}=1+\sqrt{2}

Giải Toán 9: Bài 28 trang 9 Sách bài tập Toán 9 Tập 1

So sánh (không dùng bảng số hay máy tính bỏ túi):

a.\sqrt{2}+\sqrt{3} và \sqrt{10}                    b. \sqrt{3}+2 và \sqrt{2}+\sqrt{6}

c. 16 và \sqrt{15}.\sqrt{17}                          d. 8 và \sqrt{15}+\sqrt{17}

Lời giải:

a.\sqrt{2}+\sqrt{3} và \sqrt{10}

Ta có: (\sqrt{2}+\sqrt{3})^2=2+2\sqrt{6}+3=5+2\sqrt{6}

(\sqrt{10})^2=10=5+5

So sánh 26 và 5:

Ta có: (2\sqrt{6})^2=22.(\sqrt{6})^2=4.6=24

5^2=25

Vì (2\sqrt{6})^2<52 nên 2\sqrt{6}<5

Vậy 5+2\sqrt{6}<5+5⇒(\sqrt{2}+\sqrt{3})^2<(\sqrt{10})^2⇒\sqrt{2}+\sqrt{3}<\sqrt{1}0

b.\ \sqrt{3}+2 và \sqrt{2}+\sqrt{6}

Ta có: (\sqrt{3}+2)^2=3+4\sqrt{3}+4=7+4\sqrt{3}

(\sqrt{2}+\sqrt{6})^2=2+2\sqrt{12}+6=8+2\sqrt{(4.3})=8+2.\sqrt{4}.\sqrt{3}=8+4\sqrt{3}

Vì 7+4\sqrt{3}<8+4\sqrt{3} nên (\sqrt{3}+2)^2<(\sqrt{2}+\sqrt{6})^2

Vậy \sqrt{3}+2<\sqrt{2}+\sqrt{6}

c. 16 và \sqrt{15}.\sqrt{17}

\begin{array}{l} \text { Ta có: } \sqrt{15} \cdot \sqrt{17}=\sqrt{16-1} \cdot \sqrt{16+1} \\ =\sqrt{(16-1)(16+1)}=\sqrt{16^{2}-1} \\ \text { Vi } \sqrt{16^{2}-1}=\sqrt{16^{2}} \\ \text { Vân } 16>\sqrt{15} \cdot \sqrt{17} \text { nên } 16>\sqrt{15} \cdot \sqrt{17} \end{array}

d. 8 và \sqrt{15}+\sqrt{17}

\begin{aligned} &\text { Ta có: } \quad 8^{2}=64=32+32\\ &(\sqrt{15}+\sqrt{17})^{2}=15+2 \sqrt{15.17}+17=32+2 \sqrt{15.17}\\ &\text { So sánh: } 16 \text { và } \sqrt{15.17}\\ &\text { Ta có: } \quad \sqrt{15.17}=\sqrt{(16-1)(16+1)}=\sqrt{16^{2}-1}<\sqrt{16^{2}}\\ &\text { Vì } 16>\sqrt{15.17} \text { nên } 32>2 . \sqrt{15.17}\\ &\text { Suy ra } 64>32+2 \cdot \sqrt{15.17} \Rightarrow 8^{2}>(\sqrt{15}+\sqrt{17})^{2}\\ &\text { Vậy } 8>\sqrt{15}+\sqrt{17} \end{aligned}

Giải Toán 9: Bài 29 trang 9 Sách bài tập Toán 9 Tập 1

So sánh (không dùng bảng số hay máy tính bỏ túi):

\sqrt{2003}+\sqrt{2005} và 2\sqrt{2004}

Lời giải:

\begin{array}{l} \text { Ta có: }(2 \sqrt{2004})^{2}=4.2004=4008+2.2004 \\ (\sqrt{2003}+\sqrt{2005})^{2}=2003+2 \sqrt{2003.2005}+2005 \\ =4008+2 \sqrt{2003.2005} \end{array}

\begin{aligned} &\text { So sánh } 2004 \text { và } \sqrt{2003.2005}\\ &\text { Ta có: } \quad \sqrt{2003.2005}=\sqrt{(2004-1)(2004+1)}=\sqrt{2004^{2}-1}<\sqrt{2004^{2}}\\ &\text { Suy ra: } 2004>\sqrt{2003.2005}=>2.2004>2 . \sqrt{2003.2005}\\ &\Rightarrow 4008+2.2004>4008+2 \sqrt{2003.2005}\\ &\Rightarrow(2 \sqrt{2004})^{2}>(\sqrt{2003}+\sqrt{2005})^{2}\\ &\text { Vậy } 2 \sqrt{2004}>\sqrt{2003}+\sqrt{2005} \end{aligned}

Giải Toán 9: Bài 30 trang 9 Sách bài tập Toán 9 Tập 1

Cho các biểu thức:

A=\sqrt{x+2} \cdot \sqrt{x-3} \text { và } B=\sqrt{(x+2)(x-3)}

a. Tìm x để A có nghĩa. Tìm x để B có nghĩa

b. Với giá trị nào của x thi A = B?

Lời giải:

\begin{aligned} &\text { a. } \mathrm{Ta} \operatorname{có} \mathrm{A}=\sqrt{\mathrm{x}+2} \cdot \sqrt{\mathrm{x}-3} \text { có nghĩa khi và chi khi: }\\ &\left\{\begin{array}{l} x+2 \geq 0 \\ x-3 \geq 0 \end{array} \Leftrightarrow\left\{\begin{array}{l} x \geq-2 \\ x \geq 3 \end{array} \Leftrightarrow x \geq 3\right.\right.\\ &\text { Vậy với x } \geq 3 \text { thì A có nghĩa }\\ &\mathrm{B}=\sqrt{(\mathrm{x}+2)(\mathrm{x}-3)} \text { có nghĩa khi và chi khi: }\\ &(x+2)(x-3) \geq 0\\ &\text { Truèng hop } 1:\left\{\begin{array}{l} \mathrm{x}+2 \geq 0 \\ \mathrm{x}-3 \geq 0 \end{array} \Leftrightarrow\left\{\begin{array}{l} \mathrm{x} \geq-2 \\ \mathrm{x} \geq 3 \end{array} \Leftrightarrow \mathrm{x} \geq 3\right.\right.\\ &\text {Trièng hop } 2:\left\{\begin{array}{l} x+2 \leq 0 \\ x-3 \leq 0 \end{array} \Leftrightarrow\left\{\begin{array}{l} x \leq-2 \\ x \leq 3 \end{array} \Leftrightarrow x \leq-2\right.\right. \end{aligned}

Vậy với x ≥ 3 hoặc x ≤ -2 thì B có nghĩa.

b. Để A và B đồng thời có nghĩa thì x ≥ 3

Vậy với x ≥ 3 thì A = B.

Giải Toán 9: Bài 31 trang 10 Sách bài tập Toán 9 Tập 1

Biểu diễn \sqrt{ab} ở dạng tích các căn bậc hai với a < 0 và b < 0.

Lời giải:

Vì a < 0 nên -a > 0 và b < 0 nên -b > 0

Lời giải:

Vì a < 0 nên -a > 0 và b < 0 nên -b > 0

\begin{array}{l} \text { Ta có: } \sqrt{a b}=\sqrt{(-a) \cdot(-b)}=\sqrt{-a} \cdot \sqrt{-b} \\ \text { Áp dung: } \sqrt{(-25) \cdot(-64)}=\sqrt{25} \cdot \sqrt{64}=5.8=40 \end{array}

Giải Toán 9: Bài 32 trang 10 Sách bài tập Toán 9 Tập 1

Rút gọn các biểu thức:

a. \sqrt{4(a-3)^{2}} với\ a \geq 3
b. \sqrt{9(b-2)^{2}} với b<2
c. \sqrt{a^{2}(a+1)^{2}} với a >0
d. \sqrt{b^{2}(b-1)^{2}} với b<0

Lời giải:

a. \sqrt{4(a-3)^{2}}=\sqrt{4} \sqrt{(a-3)^{2}}=2|a-3|=2(a-3) (với \left.a \geq 3\right)
b. \sqrt{9(b-2)^{2}}=\sqrt{9} \cdot \sqrt{(b-2)^{2}}=3 \cdot|b-2|=3(2-b) (với b<2)
c. \sqrt{a^{2} \cdot(a+1)^{2}}=\sqrt{a^{2}} \sqrt{(a+1)^{2}}=|a| \cdot|a+1|=a(a+1) (với .a>0)
d. \sqrt{b^{2} \cdot(b-1)^{2}}=\sqrt{b^{2}} \sqrt{(b-1)^{2}}=-b \cdot(1-b)=b(b-1) (với b<0)

Giải Toán 9: Bài 33 trang 10 Sách bài tập Toán 9 Tập 1

Tìm điều kiện của x để các biểu thức sau có nghĩa và biến đổi chúng về dạng tích:

a. \sqrt{x^{2}-4}+2 \sqrt{x-2}
b. 3 \sqrt{x+3}+\sqrt{x^{2}-9}

Lời giải:

a. Ta có: \sqrt{x^{2}-4}+2 \sqrt{x-2} có nghĩa khi và chi khi:
Ta có x^{2}-4 \geq 0 \Leftrightarrow(x+2)(x-2) \geq 0

\begin{array}{c} \text {Trường hợp } 2:\left\{\begin{array}{l} \mathrm{x}+2 \leq 0 \\ \mathrm{x}-2 \leq 0 \end{array} \Leftrightarrow\left\{\begin{array}{l} \mathrm{x} \leq-2 \\ \mathrm{x} \leq 2 \end{array}\right.\right. \\ \mathrm{x}-2 \geq 0 \Leftrightarrow \mathrm{x} \geq 2 \end{array} \Leftrightarrow \mathrm{x} \leq-2

Vậy x\ge2 thì biểu thức có nghĩa.

Biến đổi về dạng tích

\begin{aligned} \sqrt{x^{2}-4}+2 \sqrt{x-2} &=\sqrt{(x+2)(x-2)}+2 \sqrt{x-2} \\ &=\sqrt{x-2} \cdot(\sqrt{x+2}+2) \end{aligned}

Giải SBT Toán 9 bài 3: Liên hệ giữa phép nhân và phép khai phương

Giải Toán 9: Bài 33 trang 10 Sách bài tập Toán 9 Tập 1

Tìm điều kiện của x để các biểu thức sau có nghĩa và biến đổi chúng về dạng tích:

a. \sqrt{x^{2}-4}+2 \sqrt{x-2}
b. 3 \sqrt{x+3}+\sqrt{x^{2}-9}

Lời giải:

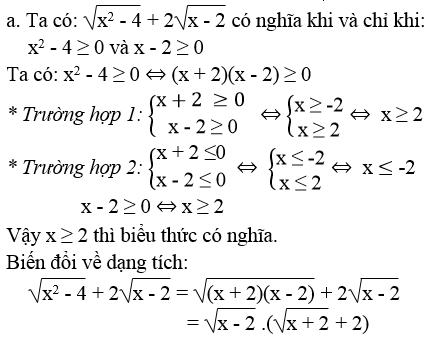
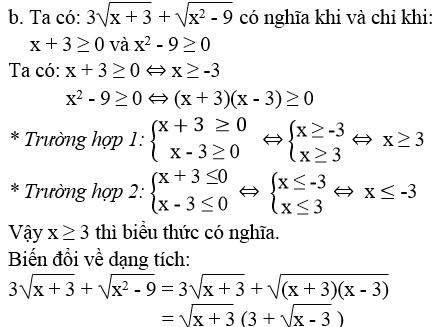
Giải SBT Toán 9 bài 3: Liên hệ giữa phép nhân và phép khai phương

Giải SBT Toán 9 bài 3: Liên hệ giữa phép nhân và phép khai phương

Giải Toán 9: Bài 34 trang 10 Sách bài tập Toán 9 Tập 1

Tìm x, biết:

a. \sqrt{x-5}=3
b. \sqrt{x-10}=-2
c. \sqrt{2 x-1}=\sqrt{5}
d. \sqrt{4-5 x}=12

Lời giải:

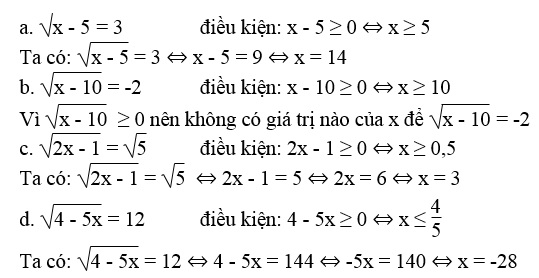
Giải SBT Toán 9 bài 3: Liên hệ giữa phép nhân và phép khai phương

Giải Toán 9: Bài 35 trang 10 Sách bài tập Toán 9 Tập 1

Với n là số tự nhiên, chứng minh:

(\sqrt{n+1}-\sqrt{n})^{2}=\sqrt{(2 n+1)^{2}}-\sqrt{(2 n+1)^{2}-1}

Viết đẳng thức trên khi n bằng 1, 2, 3, 4

Lời giải:

Ta có:

\begin{array}{l} (\sqrt{n+1}-\sqrt{n})^{2}=n+1-2 \sqrt{n(n+1)}+n=2 n+1-2 \sqrt{n(n+1)} \\ \sqrt{(2 n+1)^{2}}-\sqrt{(2 n+1)^{2}-1}=|2 n+1|-\sqrt{(2 n+1+1)(2 n+1-1)} \\ =2 n+1-\sqrt{2(n+1) 2 n}=2 n+1-\sqrt{4(n+1) n} \\ =2 n+1-\sqrt{4} \cdot \sqrt{n(n+1)}=2 n+1-2 \cdot \sqrt{n(n+1)} \end{array}

Vế trái bằng vế phải nên đẳng thức được chứng minh.

* Với n = 1, ta có: (\sqrt{2}-\sqrt{1})^2=\sqrt{9}-\sqrt{8}

* Với n = 2, ta có: (\sqrt{3}-\sqrt{2})^2=\sqrt{25}-\sqrt{24}

* Với n = 3, ta có: (\sqrt{4}-\sqrt{3})^2=\sqrt{49}-\sqrt{48}

* Với n = 4, ta có: (\sqrt{5}-\sqrt{4})^2=\sqrt{81}-\sqrt{80}

Bài tập bổ sung (trang 10)

Giải Toán 9: Bài 1 trang 10 Sách bài tập Toán 9 Tập 1

Giá trị của \sqrt{1,6}.\sqrt{2,5} bằng

A. 0,20;                    B. 2,0;

C. 20,0;                   C. 0,02.

Hãy chọn đáp án đúng.

Lời giải:

Chọn đáp án B

Trên đây VnDoc đã chia sẻ Giải SBT Toán 9 bài 3: Liên hệ giữa phép nhân và phép khai phương. Hy vọng với tài liệu này sẽ giúp ích cho các bạn học sinh tham khảo, chuẩn bị cho bài giảng sắp tới tốt hơn

.........................................

Ngoài Giải SBT Toán 9 bài 3: Liên hệ giữa phép nhân và phép khai phương. Mời các bạn học sinh còn có thể tham khảo thêm Giải bài tập Toán lớp 9, Giải vở bài tập Toán 9, soạn bài 9 hoặc đề thi học học kì 1 lớp 9, đề thi học học kì 2 lớp 9 các môn Toán, Văn, Anh, Hóa, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề thi học kì 2 lớp 9 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn học tốt

Đánh giá bài viết
5 2.197
Tìm thêm: giải bài tập sbt toán 9 giải bài tập toán 9 sbt sách bài tập toán 9
Sắp xếp theo
Xóa Đăng nhập để Gửi
    Giải SBT Toán 9
    Tải bản in

    Giải SBT Toán 9

    Xem thêm