Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

VnDoc.com

Giải SBT Toán 9 bài 5: Bảng căn bậc hai

Giải Toán 9 SBT bài 5

Bài trước

Bài sau

Giải SBT Toán 9 bài 5: Bảng căn bậc hai được VnDoc sưu tầm và đăng tải. Nội dung bám sát chương trình SBT Toán 9. Hy vọng tài liệu này sẽ giúp ích cho các bạn trả lời các câu hỏi trong sách bài tập Toán 9. Chúc các bạn học tốt, mời các bạn tham khảo

Ngoài ra, VnDoc.com đã thành lập group chia sẻ tài liệu học tập THCS miễn phí trên Facebook: Tài liệu học tập lớp 9. Mời các bạn học sinh tham gia nhóm, để có thể nhận được những tài liệu mới nhất.

Giải sách bài tập Toán 9 bài 5

Giải Toán 9: Giải Toán 9: Bài 47 trang 13 SBT Toán 9 tập 1
Giải Toán 9: Bài 48 trang 13 SBT Toán 9 tập 1
Giải Toán 9: Bài 49 trang 13 SBT Toán 9 tập 1
Giải Toán 9: Bài 50 trang 13 SBT Toán 9 tập 1
Giải Toán 9: Bài 51 trang 13 SBT Toán 9 tập 1
Giải Toán 9: Bài 52 trang 13 SBT Toán 9 tập 1
Giải Toán 9: Bài 53 trang 13 SBT Toán 9 tập 1
Giải Toán 9: Bài 54 trang 14 SBT Toán 9 tập 1
Giải Toán 9: Bài 55 trang 14 SBT Toán 9 tập 1
Giải Toán 9: Bài 5.1 phần bài tập bổ sung trang 14 SBT Toán 9 tập 1

Giải Toán 9: Bài 47 trang 13 SBT Toán 9 tập 1

Dùng bảng căn bậc hai tìm x, biết:

LG câu a

${x^2} = 15;$ ${x^2} = 15;$

Phương pháp giải:

Sử dụng ${x^2} = a$ ${x^2} = a$ suy ra $x = \sqrt a$ $x = \sqrt a$ hoặc $x = - \sqrt a$ $x = - \sqrt a$(với $a \ge 0$ $a \ge 0$).

Sử dụng bảng căn bậc hai.

Lời giải chi tiết:

Dùng bảng căn bậc hai ta có:

$\begin{array}{l} {x^2} = 15 \Leftrightarrow \left[ \begin{array}{l} x = \sqrt {15} \\ x = - \sqrt {15} \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} x = 3,873\\ x = - 3,873 \end{array} \right. \end{array}$ $\begin{array}{l} {x^2} = 15 \Leftrightarrow \left[ \begin{array}{l} x = \sqrt {15} \\ x = - \sqrt {15} \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} x = 3,873\\ x = - 3,873 \end{array} \right. \end{array}$

LG câu b

${x^2} = 22,8;$ ${x^2} = 22,8;$

Phương pháp giải:

Sử dụng ${x^2} = a$ ${x^2} = a$suy ra $x = \sqrt a$ $x = \sqrt a$ hoặc $x = - \sqrt a$ $x = - \sqrt a$ (với $a \ge 0$ $a \ge 0$).

Sử dụng bảng căn bậc hai.

Lời giải chi tiết:

$\begin{array}{l} {x^2} = 22,8 \Leftrightarrow \left[ \begin{array}{l} x = \sqrt {22,8} \\ x = - \sqrt {22,8} \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} x = 4,7749\\ x = - 4,7749 \end{array} \right. \end{array}$ $\begin{array}{l} {x^2} = 22,8 \Leftrightarrow \left[ \begin{array}{l} x = \sqrt {22,8} \\ x = - \sqrt {22,8} \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} x = 4,7749\\ x = - 4,7749 \end{array} \right. \end{array}$

LG câu c

${x^2} = 351;$ ${x^2} = 351;$

Phương pháp giải:

Sử dụng ${x^2} = a$ ${x^2} = a$ suy ra $x = \sqrt a$ $x = \sqrt a$ hoặc $x = - \sqrt a$ $x = - \sqrt a$(với $a \ge 0$ $a \ge 0$).

Sử dụng bảng căn bậc hai.

Lời giải chi tiết:

$\begin{array}{l} {x^2} = 351 \Leftrightarrow \left[ \begin{array}{l} x = \sqrt {351} \\ x = - \sqrt {351} \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} x = 18,735\\ x = - 18,735 \end{array} \right. \end{array}$ $\begin{array}{l} {x^2} = 351 \Leftrightarrow \left[ \begin{array}{l} x = \sqrt {351} \\ x = - \sqrt {351} \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} x = 18,735\\ x = - 18,735 \end{array} \right. \end{array}$

LG câu d

${x^2} = 0,46.$ ${x^2} = 0,46.$

Phương pháp giải:

Sử dụng ${x^2} = a$ ${x^2} = a$suy ra $x = \sqrt a$ $x = \sqrt a$ hoặc $x = - \sqrt a$ $x = - \sqrt a$ (với $a \ge 0$ $a \ge 0$).

Sử dụng bảng căn bậc hai.

Lời giải chi tiết:

$\begin{array}{l} {x^2} = 0,46 \Leftrightarrow \left[ \begin{array}{l} x = \sqrt {0,46} \\ x = - \sqrt {0,46} \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} x = 0,6782\\ x = - 0,6782 \end{array} \right. \end{array}$ $\begin{array}{l} {x^2} = 0,46 \Leftrightarrow \left[ \begin{array}{l} x = \sqrt {0,46} \\ x = - \sqrt {0,46} \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} x = 0,6782\\ x = - 0,6782 \end{array} \right. \end{array}$

Giải Toán 9: Bài 48 trang 13 SBT Toán 9 tập 1

Lựa chọn câu để xem lời giải nhanh hơn

Dùng bảng bình phương tìm x, biết:

LG câu a

$\sqrt x = 1,5;$ $\sqrt x = 1,5;$

Phương pháp giải:

Dùng bảng bình phương để tìm x.

ÁP dụng: Với $A \ge 0;B \ge 0$ $A \ge 0;B \ge 0$

$\sqrt A = B \Leftrightarrow A = {B^2}.$ $\sqrt A = B \Leftrightarrow A = {B^2}.$

Lời giải chi tiết:

$\sqrt x = 1,5 \Rightarrow x=1,5^2\Rightarrow x = 2,25$ $\sqrt x = 1,5 \Rightarrow x=1,5^2\Rightarrow x = 2,25$

LG câu b

$\sqrt x = 2,15;$ $\sqrt x = 2,15;$

Phương pháp giải:

Dùng bảng bình phương để tìm x.

ÁP dụng: Với $A \ge 0;B \ge 0$ $A \ge 0;B \ge 0$

$\sqrt A = B \Leftrightarrow A = {B^2}.$ $\sqrt A = B \Leftrightarrow A = {B^2}.$

Lời giải chi tiết:

$\sqrt x = 2,15 \Rightarrow x=2,15^2\Rightarrow x \approx 4,623$ $\sqrt x = 2,15 \Rightarrow x=2,15^2\Rightarrow x \approx 4,623$

LG câu c

$\sqrt x = 0,52;$ $\sqrt x = 0,52;$

Phương pháp giải:

Dùng bảng bình phương để tìm x.

ÁP dụng: Với $A \ge 0;B \ge 0$ $A \ge 0;B \ge 0$

$\sqrt A = B \Leftrightarrow A = {B^2}.$ $\sqrt A = B \Leftrightarrow A = {B^2}.$

Lời giải chi tiết:

$\sqrt x = 0,52 \Rightarrow x=0,52^2 \Rightarrow x \approx 0,2704;$ $\sqrt x = 0,52 \Rightarrow x=0,52^2 \Rightarrow x \approx 0,2704;$

LG câu d

$\sqrt x = 0,038.$ $\sqrt x = 0,038.$

Phương pháp giải:

Dùng bảng bình phương để tìm x.

ÁP dụng: Với $A \ge 0;B \ge 0$ $A \ge 0;B \ge 0$

$\sqrt A = B \Leftrightarrow A = {B^2}.$ $\sqrt A = B \Leftrightarrow A = {B^2}.$

Lời giải chi tiết:

$\sqrt x = 0,038 \Rightarrow x=0,038^2 \Rightarrow x \approx 0,0014.$ $\sqrt x = 0,038 \Rightarrow x=0,038^2 \Rightarrow x \approx 0,0014.$

Giải Toán 9: Bài 49 trang 13 SBT Toán 9 tập 1

Đề bài

Kiểm tra kết quả bài 47, 48 bằng máy tính bỏ túi.

Sử dụng máy tính bỏ túi để kiểm tra kết quá

Lời giải chi tiết

Ví dụ: Với câu a) bài 47, ta có:

$\eqalign{ & {x^2} = 15 \Rightarrow {x_1} = \sqrt {15} \cr & \approx 3,872983346 \approx 3,873 \cr}$ $\eqalign{ & {x^2} = 15 \Rightarrow {x_1} = \sqrt {15} \cr & \approx 3,872983346 \approx 3,873 \cr}$

$\eqalign{ & {x_2} = - \sqrt {15} \approx - 3,872983346 \cr & \approx - 3,873 \cr}$ $\eqalign{ & {x_2} = - \sqrt {15} \approx - 3,872983346 \cr & \approx - 3,873 \cr}$

Tương tự với các câu tiếp theo.

Giải Toán 9: Bài 50 trang 13 SBT Toán 9 tập 1

Đề bài

Thử lại kết quả bài 47 bằng bảng bình phương.

Lời giải chi tiết

Với câu a) bài 47 ta có ${x^2} = 15$ ${x^2} = 15$

Tìm ô có giá trị gần với 15 trong bảng bình phương ta được ô 14,98 và ô 15,05

* Với ô 14,98 tra bảng ta được $x \approx 3,87$ $x \approx 3,87$. Đây là kết quả gần đúng nhưng hơi thiếu.

* Với ô 15,05 tra bảng ta được $x \approx 3,88$ $x \approx 3,88$. Đây là kết quả gần đúng nhưng hơi thừa.

Thực hiện tương tự cho các bài còn lại.

Giải Toán 9: Bài 51 trang 13 SBT Toán 9 tập 1

Giải bài 51 trang 13 SBT Toán 9. Thử lại kết quả bài 48 bằng bảng căn bậc hai.

Đề bài

Thử lại kết quả bài 48 bằng bảng căn bậc hai.

Lời giải chi tiết

Sử dụng bảng căn bậc hai, thử lại các kết quả bằng cách tra bảng căn bậc hai cho các kết quả vừa tìm được ở bài 48.

Giải Toán 9: Bài 52 trang 13 SBT Toán 9 tập 1

Giải bài 52 trang 13 sách bài tập Toán 9. Điền vào chỗ trống (...) trong cách chứng minh sau: số căn 2 là số vô tỉ...

Đề bài

Điền vào các chỗ trống (...) trong phép chứng minh sau:

Số $\sqrt 2$ $\sqrt 2$ là số vô tỉ.

Giả sử $\sqrt 2$ $\sqrt 2$ không phải là số vô tỉ thì phải tồn tại các số nguyên m và n sao cho $\sqrt 2 = \dfrac{m}{n}$ $\sqrt 2 = \dfrac{m}{n}$, trong đó n > 0 còn hai số m và n không có ước chung nào khác 1 và -1 (hai số m và n nguyên tố cùng nhau).

Khi đó, ta có: ... hay $2{n^2} = {m^2} (1).$ $2{n^2} = {m^2} (1).$

Kết quả (1) chứng tỏ m là số chẵn, nghĩa là m = 2p với p là số nguyên.

Thay m = 2p vào (1) ta được: ... hay ${n^2} = 2{p^2} (2)$ ${n^2} = 2{p^2} (2)$

Kết quả (2) chứng tỏ n phải là số chẵn.

Hai số m và n đều là số chẵn, trái với giả thiết m và n không có ước chung nào khác 1 và -1.

Vậy $\sqrt 2$ $\sqrt 2$ là số vô tỉ.

Giải Toán 9: Bài 53 trang 13 SBT Toán 9 tập 1

Lựa chọn câu để xem lời giải nhanh hơn

Chứng minh:

LG câu a

Số $\sqrt 3$ $\sqrt 3$ là số vô tỉ;

Lời giải chi tiết:

Giả sử $\displaystyle\sqrt 3$ $\displaystyle\sqrt 3$ không phải là số vô tỉ. Khi đó tồn tại các số nguyên a và b sao cho $\displaystyle \displaystyle\sqrt 3 = {a \over b}$ $\displaystyle \displaystyle\sqrt 3 = {a \over b}$ với b > 0. Hai số a và b không có ước chung nào khác 1 và -1.

Ta có: $\displaystyle{\left( {\sqrt 3 } \right)^2} = {\left( {{a \over b}} \right)^2}$ $\displaystyle{\left( {\sqrt 3 } \right)^2} = {\left( {{a \over b}} \right)^2}$ hay $\displaystyle{a^2} = 3{b^2} (1)$ $\displaystyle{a^2} = 3{b^2} (1)$

Kết quả trên chứng tỏ a chia hết cho 3, nghĩa là ta có a = 3c với c là số nguyên.

Thay a = 3c vào (1) ta được: $\displaystyle{\left( {3c} \right)^2} = 3{b^2}$ $\displaystyle{\left( {3c} \right)^2} = 3{b^2}$ hay $\displaystyle{b^2} = 3{c^2}$ $\displaystyle{b^2} = 3{c^2}$

Kết quả trên chứng tỏ b chia hết cho 3.

Hai số a và b đều chia hết cho 3, trái với giả thiết a và b không có ước chung nào khác 1 và -1.

Vậy $\displaystyle\sqrt 3$ $\displaystyle\sqrt 3$ là số vô tỉ.

LG câu b

Các số $5\sqrt 2 ;\ 5\sqrt 2$ $5\sqrt 2 ;\ 5\sqrt 2$ đều là số vô tỉ.

Lời giải chi tiết:

Giả sử $\displaystyle5\sqrt 2$ $\displaystyle5\sqrt 2$ là số hữu tỉ, nghĩa là tồn tại số hữu tỉ a sao cho $\displaystyle 5\sqrt 2 = a.$ $\displaystyle 5\sqrt 2 = a.$

Suy ra: $\displaystyle\sqrt 2 = {a \over 5}$ $\displaystyle\sqrt 2 = {a \over 5}$ hay $\displaystyle\sqrt 2$ $\displaystyle\sqrt 2$ là số hữu tỉ.

Điều này vô lí vì $\displaystyle\sqrt 2$ $\displaystyle\sqrt 2$ là số vô tỉ (theo bài 52 trang 13 SBT toán 9 tập 1)

Vậy $\displaystyle5\sqrt 2$ $\displaystyle5\sqrt 2$ là số vô tỉ.

*Giả sử $\displaystyle3 + \sqrt 2$ $\displaystyle3 + \sqrt 2$ là số hữu tỉ, nghĩa là tồn tại một số hữu tỉ b mà: $\displaystyle3 + \sqrt 2 = b$ $\displaystyle3 + \sqrt 2 = b$

Suy ra: $\displaystyle\sqrt 2 = b - 3$ $\displaystyle\sqrt 2 = b - 3$ hay $\displaystyle\sqrt 2$ $\displaystyle\sqrt 2$ là số hữu tỉ.

Điều này vô lí vì $\displaystyle\sqrt 2$ $\displaystyle\sqrt 2$ là số vô tỉ (theo bài 52 trang 13 SBT toán 9 tập 1)

Vậy $\displaystyle3 + \sqrt 2$ $\displaystyle3 + \sqrt 2$ là số vô tỉ.

Giải Toán 9: Bài 54 trang 14 SBT Toán 9 tập 1

Đề bài

Tìm tập hợp các số x thỏa mãn bất đẳng thức: $\sqrt x > 2$ $\sqrt x > 2$ và biểu diễn tập hợp đó trên trục số.

Phương pháp giải

Áp dụng: Với $A \ge 0;B \ge 0$ $A \ge 0;B \ge 0$ ta có:

$\sqrt A > \sqrt B \Leftrightarrow A>B.$ $\sqrt A > \sqrt B \Leftrightarrow A>B.$

Lời giải chi tiết

Điều kiện: $x \ge 0$ $x \ge 0$

Ta có: $\sqrt x > 2 \Leftrightarrow \sqrt x > \sqrt 4 \Leftrightarrow x > 4.$ $\sqrt x > 2 \Leftrightarrow \sqrt x > \sqrt 4 \Leftrightarrow x > 4.$

Biểu diễn trên trục số:

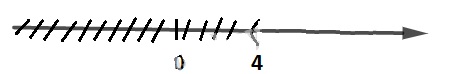
Giải SBT Toán 9 bài 5: Bảng căn bậc hai

Giải Toán 9: Bài 55 trang 14 SBT Toán 9 tập 1

Đề bài

Tìm tập hợp các số x thỏa mãn bất đẳng thức:

$\sqrt x < 3$ $\sqrt x < 3$

và biểu diễn tập hợp đó trên trục số.

Lời giải chi tiết

Điều kiện: $x \ge 0$ $x \ge 0$

Ta có: $\sqrt x < 3 \Leftrightarrow \sqrt x < \sqrt 9 \Leftrightarrow x < 9$ $\sqrt x < 3 \Leftrightarrow \sqrt x < \sqrt 9 \Leftrightarrow x < 9$

Suy ra $0\le x<9.$ $0\le x<9.$

Biểu diễn trên trục số:

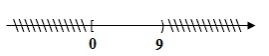
Giải SBT Toán 9 bài 5: Bảng căn bậc hai

Giải Toán 9: Bài 5.1 phần bài tập bổ sung trang 14 SBT Toán 9 tập 1

Đề bài

Tra bảng căn bậc hai, tìm $\sqrt {35,92}$ $\sqrt {35,92}$được $\sqrt {35,92} \approx 5,993$ $\sqrt {35,92} \approx 5,993$. Vậy suy ra $\sqrt {0,3592}$ $\sqrt {0,3592}$ có giá trị gần đúng là:

(A) 0,5993

(B) 5,993

(D) 599,3

Phương pháp giải

Sử dụng bảng tra căn bậc hai.

Hoặc sử dụng: $\sqrt {\dfrac{A}{B}}=\dfrac{\sqrt {A}}{\sqrt {B}}$ $\sqrt {\dfrac{A}{B}}=\dfrac{\sqrt {A}}{\sqrt {B}}$ với $A\ge 0;B> 0$ $A\ge 0;B> 0$

Lời giải chi tiết

Ta có: $\sqrt {0,3592}=\sqrt {\dfrac{35,92}{100}}=\dfrac{\sqrt {35,92}}{\sqrt {100}}\approx\dfrac{5,993}{10}=0,5993$ $\sqrt {0,3592}=\sqrt {\dfrac{35,92}{100}}=\dfrac{\sqrt {35,92}}{\sqrt {100}}\approx\dfrac{5,993}{10}=0,5993$

Cách khác: Tra bảng căn bậc hai ta có: $\sqrt {0,3592} \approx 0,5993$ $\sqrt {0,3592} \approx 0,5993$

Chọn đáp án (A).

Trên đây VnDoc đã chia sẻ Giải SBT Toán 9 bài 5: Bảng căn bậc hai. Hy vọng với tài liệu này sẽ giúp ích cho các bạn học sinh tham khảo, chuẩn bị cho bài giảng sắp tới tốt hơn

.........................................

Ngoài Giải SBT Toán 9 bài 5: Bảng căn bậc hai. Mời các bạn học sinh còn có thể tham khảo thêm Giải bài tập Toán lớp 9, Giải vở bài tập Toán 9, soạn bài 9 hoặc đề thi học học kì 1 lớp 9, đề thi học học kì 2 lớp 9 các môn Toán, Văn, Anh, Hóa, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề thi học kì 2 lớp 9 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn học tốt