Đề thi giữa học kì 1 Toán 9 Kết nối tri thức (Cấu trúc mới) Đề 5

Kỳ thi giữa học kì 1 là thời điểm quan trọng để học sinh lớp 9 kiểm tra lại mức độ nắm vững kiến thức và rèn luyện kỹ năng giải bài. Đặc biệt, với bộ sách Kết nối tri thức, cấu trúc đề thi được thiết kế khoa học, bám sát chương trình học, đồng thời mở rộng với nhiều dạng bài tập rèn tư duy logic và khả năng vận dụng thực tế.

Trong bài viết này, chúng tôi giới thiệu Đề thi giữa học kì 1 Toán 9 Kết nối tri thức (Cấu trúc mới) – Đề 5 kèm đáp án chi tiết, giúp học sinh không chỉ làm quen với dạng đề chuẩn mà còn có thể tự kiểm tra, đối chiếu kết quả. Tài liệu là công cụ hữu ích để luyện tập, củng cố kiến thức và chuẩn bị tốt nhất cho kỳ thi quan trọng.

Họ và tên học sinh: …………………………….. Lớp: …………………………..

PHẦN I. PHẦN TRẮC NGHIỆM KHÁCH QUAN NHIỀU LỰA CHỌN (3,0 ĐIỂM)

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn 1 phương án.

Câu 1: Phương trình nào sau đây KHÔNG là phương trình bậc nhất hai ẩn?

A. x – 2y = 5.                                    B. 0x + 0y = –3.

C. 6x + 0y = 1.                                  D. 0x – 4y = 3.

Câu 2: Phương trình nào sau đây là phương trình tích?

A. \((x - 3)(3x + 1) = 2\).                          B. \((x - 3)(2x + 3) = (x - 3)\).

C. \((x - 3)(2x + 3) = (x - 3)\).                     D. \((x - 5)(x + 1) = 0\).

Câu 3: Cặp số \(\left( x_{0};y_{0} \right)\)là một nghiệm của hệ phương trình \(\left\{ \begin{matrix} ax + by = c\ \ \ \ \ (1) \\ a'x + b'y = c'\ (2) \end{matrix} \right.\)nếu

A. \(\left( x_{0};y_{0} \right)\) là nghiệm của phương trình \((1)\).

B. \(\left( x_{0};y_{0} \right)\) là nghiệm của phương trình \((2)\).

C. \(\left( x_{0};y_{0} \right)\) là nghiệm của một trong hai phương trình.

D. \(\left( x_{0};y_{0} \right)\) là nghiệm chung của hai phương trình \((1)\)và \((2)\).

Câu 4: Cặp số nào sau đây là nghiệm của hệ phương trình 

A. (2 ; 1).              B. (2 ; -1).            C. (1 ; - 1).            D. (1 ; 1).

Câu 5: Cho \(a < b\) khi đó bất đẳng thức đúng là:

A. \(2a - 1 < 2b - 3\).                   B. \(- 3a + 2 > - 3b - 1\).

C. \(2a + 1 > 2b + 1\).                    D. \(3a - 1 < - 3b + 3\).

Câu 6: Bất phương trình dạng \(ax + b > 0\)(hoặc \(ax + b < 0,\ ax + b \geq 0,ax + b \leq 0\)) là bất phương trình bậc nhất một ẩn (ẩn là \(x\)) với điều kiện:

A. \(a,\ b\) là hai số đã cho.           B. \(a,\ b\) là hai số đã cho và \(a\) khác \(0\).

C. \(a\) khác \(0\).                              D. \(a\) và \(b\) khác \(0\).

Câu 7: Cặp số \(( - 2; - 3)\) là nghiệm của phương trình sau đây?

A. \(\left\{ \begin{matrix} x - 2y = 3 \\ 2x + y = 4 \end{matrix} \right.\)           B. \(\left\{ \begin{matrix} 2x - y = - 1 \\ x - 3y = 8 \end{matrix} \right.\)     C. \(\left\{ \begin{matrix} 2x - y = - 1 \\ x - 3y = 7 \end{matrix} \right.\)         D. \(\left\{ \begin{matrix} 4x - 2y = 0 \\ x - 3y = 5 \end{matrix} \right.\)

Câu 8: Điều kiện xác định của phương trình \(\frac{1 - 2x}{x^{2}} = \frac{1}{2}\) là: 

A. \(x \neq \frac{1}{2}\).                     B. \(x \neq 0\).           C. \(x \neq 2\).                      D. \(x \neq \frac{1}{2}\) và \(x \neq 0\).

Câu 9: Cho tam giác DEF có \(\widehat{D} = 90^{0}\), \(\sin\widehat{E}\) bằng:

A. \(\frac{DE}{EF}\)             B. \(\frac{DI}{DE}\)                C. \(\frac{DI}{EI}\)                  D. \(\frac{DF}{ DE}\)

Câu 10: Cho tam giác \(ABC\) vuông tại \(A\):

A. \(\tan B = \frac{AC}{BC}\)                     B. \(cotB = \frac{AC}{BC}\)

C. \(\sin B = \frac{AB}{BC}\)                             D. \(\sin B = \frac{AB}{AC}\)

Cho hình vẽ dưới đây, trả lời các câu hỏi 11 và 12

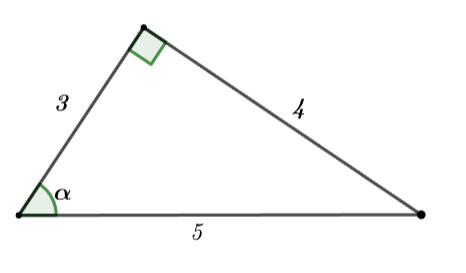
Câu 11: tan α bằng:

A. \(\frac{4}{3}\)              B. \(\frac{3}{4}\)               C. \(\frac{3}{5}\)                 D. \(\frac{4}{5}\)

Câu 12: sin α bằng:

A. \(\frac{4}{3}\)                  B. \(\frac{3}{4}\)                      C. \(\frac{3}{5}\)                D. \(\frac{4}{5}\)

PHẦN II. PHẦN TRẮC NGHIỆM ĐÚNG SAI (2,0 ĐIỂM)

Thí sinh trả lời câu 1 và câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh trả lời đúng hoặc sai.

Câu 1: Xét sự đúng sai của các khẳng định dưới đây?

a) Phương trình \((x - 2)(x + 3) = 0\) là phương trình tích.

b) Phương trình \((x - 2)(x + 3) = 2\) là phương trình tích.

c) Phương trình \((x - 2)\left( x^{2} + 3 \right) = 0\) chỉ có \(1\) nghiệm.

d) Phương trình \(- 4(x + 3) = 0\) chỉ có \(2\) nghiệm.

Câu 2: Xét sự đúng sai của các nhận định dưới đây?

a) Hai bất đẳng thức \(2a - 1 < 2\)và \(3a - 3 > 4\)là hai bất đẳng thức ngược chiều.

b) Nếu có \(a \leq b\) thì \(- 3a \geq - 3b\).

c) Nếu \(a \geq b\) thì \(- 2 - a \geq - 2 - b\).

d) Nếu \(2a - 3 < 2b - 4\)thì \(a > b\).

PHẦN III. TỰ LUẬN (5,0 ĐIỂM)

Câu 1: Giải phương trình, hệ phương trình và bất phương trình dưới đây:

a) \(\left\{ \begin{matrix} 0,2x + 0,1y = 0,3 \\ 3x + y = 5 \end{matrix} \right.\)                  b) \(\frac{x - 3}{x - 5} + \frac{1}{x} = \frac{x + 5}{x(x - 5)}\)

c) \(5(x - 3) + 7 > 2(x + 3) - 11\)

Câu 2: Giải bài toán bằng cách lập hệ phương trình

Một cano đi xuôi dòng từ địa điểm \(A\) đến địa điểm \(B\) và lại ngược dòng từ địa điểm \(B\) về địa điểm \(A\) mất \(9\) giờ, tốc độ của cano khi nước yên lặng không đổi trên suốt quãng đường đó và tốc độ của dòng nước cũng không đỏi khi cano chuyển động. Biết thời gian cano đi xuôi dòng \(5km\) bằng thời gian cano đi ngược dòng \(4km\) và quãng đường \(AB\) dài \(160km\). Tính tốc độ của cano khi nước yên lặng và tốc độ của dòng nước.

Câu 3. Ca nô dù bay là một trò chơi thể thao mạo hiểm được ưa chuộng trong đó người chơi được đeo dù và được canô kéo bay lên để thưởng ngoạn cảnh biển từ trên cao (xem hình vẽ). Biết độ dài của dây kéo \(AC = 160\ m\) và góc tạo bởi dây kéo và phương nằm ngang \(\widehat{ACB} = 25{^\circ}\).

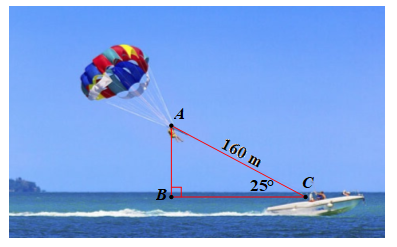
a) Tính độ cao \(AB\) của người chơi so với mặt biển.

b) Muốn bay cao \(75\ m\) thì dây kéo phải dài bao nhiêu mét (làm tròn kết quả đến hàng phần mười mét)?

Câu 4. Người ta dùng 100 m rào để rào một mảnh vườn hình chữ nhật để thả gia súc. Biết một cạnh của hình chữ nhật là bức tường (không phải rào). Tính diện tích lớn nhất của mảnh vườn để có thể rào được.

------------------- Hết ----------------------

Toàn bộ nội dung đã sẵn sàng! Nhấn Tải về để tải đầy đủ tài liệu.

-----------------------------------------------------------

Đề thi giữa học kì 1 Toán 9 Kết nối tri thức (Cấu trúc mới) – Đề 5 mang đến cho học sinh cơ hội rèn luyện nhiều dạng toán khác nhau, từ cơ bản đến nâng cao. Việc luyện tập thường xuyên với đề thi kèm đáp án chi tiết không chỉ giúp củng cố kỹ năng mà còn tăng sự tự tin khi bước vào phòng thi.

Hy vọng rằng bộ đề này sẽ là người bạn đồng hành đáng tin cậy trong quá trình ôn tập của các em học sinh lớp 9. Hãy kết hợp việc học lý thuyết với luyện nhiều đề thi khác nhau để đạt hiệu quả tối đa, nắm chắc kiến thức và chinh phục điểm số cao trong kỳ thi giữa học kì.