Đề thi giữa học kì 2 môn Toán lớp 8 phòng GD&ĐT Bình Giang, Hải Dương năm 2014 - 2015

Đề thi giữa học kì 2 môn Toán lớp 8

Đề thi giữa học kì 2 môn Toán lớp 8 phòng GD&ĐT Bình Giang, Hải Dương năm 2014 - 2015 là tài liệu luyện thi giữa học kỳ 2 lớp 8 rất hiệu quả. Đây cũng là tài liệu tham khảo môn Toán giúp các bạn học sinh lớp 8 ôn tập lại kiến thức, nhằm học tập môn Toán tốt hơn, đạt điểm cao trong bài thi giữa kì, thi cuối kì. Mời các bạn tham khảo.

Đề thi giữa học kì 2 môn Toán hình học lớp 8 Phòng GD&ĐT Bình Giang, Hải Dương năm học 2015 - 2016

Đề thi giữa học kì 2 môn Toán đại số lớp 8 Phòng GD&ĐT Bình Giang, Hải Dương năm học 2015 - 2016

Đề thi giữa học kì 2 môn Toán lớp 8 trường THCS Cự Khê, Hà Nội năm học 2015 - 2016

Đề thi học kì 2 môn Toán lớp 8 trường THCS Đồng Mai, Hà Nội năm 2014 - 2015

Đề thi giữa học kì 2 môn Ngữ văn lớp 8 trường THCS Tam Hưng, Thanh Oai năm 2015 - 2016

PHÒNG GD&ĐT BÌNH GIANG

ĐỀ KIỂM TRA ĐỊNH KỲ GIỮA KỲ II NĂM HỌC: 2014 - 2015 MÔN: ĐẠI SỐ - LỚP 8 Thời gian làm bài: 45 phút (Đề bài gồm 01 trang)

ĐẠI SỐ:

Câu 1 (4,0 điểm). Giải các phương trình:
1) 3x - 12 = 0

3) (x + 3)(2x - 4) = 0

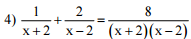
Câu 2 (2,0 điểm). Cho a < b, hãy so sánh:

1) a + 2 và b + 2 2) a - 3 và b - 3

3) -3a và -3b 4) 2a + 1 và 2b + 1

Câu 3 (2,0 điểm). So sánh a và b nếu:

1) a + 5 > b + 5

3) 2 - a ≤ 2- b

Câu 4 (2,0 điểm). Giải bài toán bằng cách lập phương trình:

Một canô xuôi dòng từ bến A đến bến B mất 3 giờ và ngược dòng từ bến B về bến A mất 4 giờ. Tính khoảng cách giữa hai bến A và B, biết vận tốc của dòng nước là 2,5 km/h.

Đáp án đề thi giữa học kì 2 môn Toán lớp 8

Câu 1:

1) 3x - 12 = 0 <=> 3x = 12 <=> x = 4 (0,75đ)

Vậy phương trình có tập nghiệm S = {4} (0,25đ)

4x = 3(x + 2) <=> 4x = 3x + 6 (0,5đ)

<=> x = 6. Vậy phương trình có tập nghiệm là S = {6} (0,5đ)

3) (x +3)(2x + 4) = 0 <=> x + 3 = 0 hoặc 2x - 4 = 0 <=> x = -3 hoặc 2x = 4 (0,5đ)

<=> x = -3 hoặc x = 2. Vậy phương trình có tập nghiệm là S ={-3; 2} (0,5đ)

4) ĐKXĐ: x ≠ 2; x ≠ - 2; x - 2 + 2(x-2) = 8 (0,5đ)

<=> x - 2 + 2x + 4 = 8 <=> 3x + 2 = 8 <=> x = 2 (loại). Vậy phương trình đã cho vô nghiệm (0,5đ)

Câu 2:

1) Do a < b => a + 2 < b + 2 (liên hệ giữa thứ tự và phép cộng) (0,5đ)

2) Do a< b => a + (-3) < b + (-3) => a - 3 < b - 3 (liên hệ giữa thứ tự và phép cộng) (0,5đ)

3) Do a < b => (-3)a > (-3)b => -3a > -3b (liên hệ giữa thứ tự và phép nhân) (0,5đ)

4) Do a < b => 2a < 2b (liên hệ giữa thứ tự và phép nhân) (0,25đ)

=>2a + 1 < 2b + 1 (liên hệ giữa thứ tự và phép cộng) (0,25đ)

Câu 3:

1) a + 5 > b + 5 => a + 5 + (-5) > b + 5 + (-5) (liên hệ giữa thứ tự và phép cộng) (0,25đ)

=> a > b Vậy a > b. (0,25đ)

=> a < b. Vậy a < b (0,25đ)

3) 2 - a ≤ 2 - b => 2 - a + (-2) ≤ 2 - b + (-2) (liên hệ giữa thứ tự và phép cộng ) (0,25đ)

=> -a ≤ -b => a ≥ b. Vậy a = b (0,25đ)

=> 2a² + 2b² = a² + 2ab + b² (0,25đ)

=> a² - 2ab + b² = 0 => (a - b) 2 = 0 => a = b. Vậy a = b (0,25đ)

Câu 4:

Gọi khoảng cách giữa hai bến tàu là A và B là x (km), điều kiện: a > 0 (0,25đ)

Vận tốc ca nô đi từ A đến B là x/3 (km/h) (0,25đ)

Vận tốc ca nô đi từ B về A là x/4 (km/h) (0,25đ)

Do vận tốc của dòng nước là 2,5 km/h, vận tốc thực cano không đổi nên ta có pt:

<=> 4x - 30 = 3x + 30 (0,25đ)

<=> x = 60 (thỏa mãn điều kiện) (0,25đ)

Vậy khoảng cách giữa hai bến A và B là 60km (0,25đ)

1) a 2  và b 2  ; 2) a 3  và b 3  ; 3) 3a và 3b ; 4) 2a 1  và 2b 1