Đề cương ôn tập Hình học lớp 7
Đề cương ôn tập Hình học lớp 7
Đề cương ôn tập Hình học lớp 7 khái quát nội dung học trong học kì 1 và học kì 2 môn Toán lớp 7 phần Hình học, giúp các bạn học sinh ôn tập và củng cố lại kiến thức về Hình học lớp 7 đồng thời nắm vững các kiến thức để chuẩn bị cho các kì thi học kì lớp 7 sắp tới. Sau đây là Nội dung của đề cương ôn tập Hình học lớp 7, mời các bạn tham khảo.
Trong phần toán hình học học kỳ II lớp 7, các em cần ôn tập kĩ một số kiến thức sau:
1. Góc và đường thẳng song song
1.1. Góc ở vị trí đặc biệt. Tia phân giác của một góc
1.2. Hai đường thẳng song song
1.3. Tiên đề Euclid
1.4. Định lí và chứng minh định lí
2. Tam giác bằng nhau
2.1. Tổng các góc của một tam giác
2.2. Các trường hợp bằng nhau của hai tam giác:
• Cạnh – cạnh – cạnh (c . c . c)
• Cạnh – góc – cạnh (c . g . c)
• Góc – cạnh – góc (g . c . g)
2.3. Tam giác cân
a) Tam giác cân là tam giác có 2 cạnh bằng nhau.
b) Tính chất: Trong một tam giác cân, hai góc đáy bằng nhau.
c) Dấu hiệu nhận biết:
• Nếu một tam giác có 2 cạnh bằng nhau ⇒ Tam giác đó là tam giác cân.
• Nếu một tam giác có 2 góc bằng nhau ⇒ Tam giác đó là tam giác cân.
2.4. Tam giác đều
a) Tam giác đều là tam giác có 3 cạnh bằng nhau.
b) Tính chất: Trong một tam giác đều, mỗi góc bằng 60o
c) Dấu hiệu nhận biết:
• Nếu tam giác có 3 cạnh bằng nhau ⇒ Tam giác đó là tam giác đều.
• Nếu tam giác có 3 góc bằng nhau ⇒ Tam giác đó là tam giác đều.
• Nếu một tam giác cân có 1 góc nhọn bằng 60o ⇒ Tam giác đó là tam giác đều.
3. Quan hệ giữa các yếu tố trong một tam giác
3.1. Quan hệ cạnh góc trong một tam giác:
Trong một tam giác:
• Góc đối diện cùng với cạnh lớn hơn là góc lớn hơn
• Cạnh đối diện cùng với góc lớn hơn là cạnh lớn hơn
3.2. Quan hệ giữa đường xiên và hình chiếu | đường vuông góc và đường xiên
a) Từ điểm A không nằm trên đường thẳng d, kẻ một đường thẳng vuông góc cùng với d tại H. Khi đó:
• Đoạn thẳng AH được gọi là đường vuông góc hay đoạn vuông góc kẻ từ điểm A tới đường thẳng d; điểm H gọi là chân của đường vuông góc hay hình chiếu của A trên đường thẳng d.
• Đoạn thẳng AB được gọi là một đường xiên kẻ từ điểm A tới đường thẳng d.
• Đoạn thẳng HB được gọi là hình chiếu của đường xiên AB ở trên đường thẳng d.
b) Quan hệ giữa Đường vuông góc & Đường xiên
Trong các Đường vuông góc & Đường xiên kẻ từ một điểm nằm ngoài một đường thẳng tới đường thẳng đó, đường vuông góc là đường thẳng ngắn nhất.
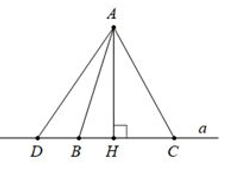
• Các đường xiên & Hình chiếu của chúng
3.3. Bất đẳng thức trong tam giác
Định lý: Trong một tam giác, tổng độ dài của hai cạnh bất kỳ bao giờ cũng lớn hơn độ dài của cạnh còn lại.
3.4. Tính chất 3 đường trung tuyến
Định lý:
– Giao điểm của 3 đường trung tuyến của tam giác được gọi là trọng tâm.
– 3 đường trung tuyến của tam giác cùng đi qua một điểm. Điểm đó cách đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy.
Ví dụ: Với G là trọng tâm của tam giác ABC:
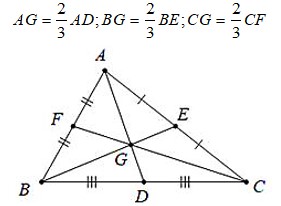
3.5. Tính chất phân giác của một góc
Tia phân giác của một góc chia góc đó trở thành 2 góc nhỏ có số đo bằng nhau và bằng một nửa (1/2) góc ban đầu. Tất cả các điểm nằm ở trên tia phân giác của một góc sẽ cách đều 2 tia tạo thành góc.
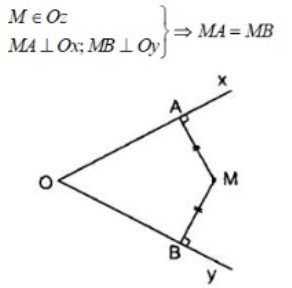
3.6. Tính chất 3 đường phân giác trong tam giác
Trong tam giác cân, đường phân giác xuất phát từ đỉnh đối diện cùng với đáy đồng thời là đường trung tuyến ứng với cạnh đáy. Ba đường phân giác của một Δ cùng đi qua một điểm. Điểm này cách đều 3 cạnh của tam giác đó.
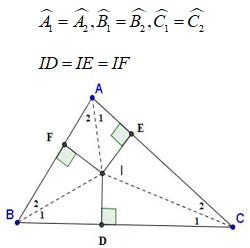
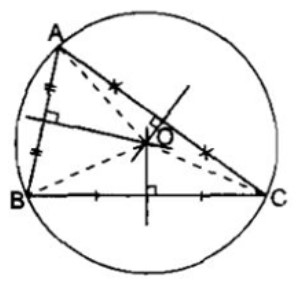
3.7. Tính chất 3 đường trung trực của tam giác
Trong tam giác, 3 đường trung trực đồng quy tại một điểm, điểm đó cách đều 3 đỉnh của Δ và là tâm của đường tròn ngoại tiếp tam giác ấy.
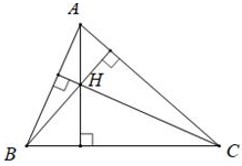
3.8. Tính chất 3 đường cao trong một tam giác
Ba đường cao của Δ cùng đi qua một điểm. Điểm đó được gọi là trực tâm của tam giác.
Ví dụ: H là giao điểm của 3 đường cao của tam giác ABC. H là trực tâm của ΔABC
4. Một số hình khối trong thực tiễn
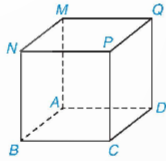
4.1. Hình hộp chữ nhật và hình lập phương
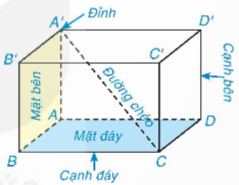
a) Các kích thước của hình hộp chữ nhật là a, b, c (cùng đơn vị độ dài) thì:
• Diện tích xung quanh: Sxq = 2(a + b).c
• Diện tích toàn phần: Stp = Sxq + 2Sđ
• Thể tích: V = abc
b) Kích thước của hình lập phương cạnh a là:
• Diện tích xung quanh: S = 4a2
• Diện tích toàn phần: S = 6a2
• Thể tích: V = a3
4.2. Hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác.
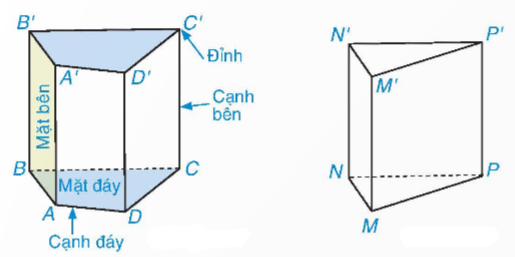
a) Trong hình lăng trụ đứng tam giác (tứ giác):
- Hai mặt đáy song song với nhau.
- Các mặt bên là những hình chữ nhật.
- Các cạnh bên song song và bằng nhau.
Độ dài một cạnh bên gọi là chiều cao của lăng trụ đứng.
* Chú ý: Hình hộp chữ nhật và hình lập phương cũng là các hình lăng trụ đứng tứ giác.
b) Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác.
• Diện tích xung quanh của lăng trụ đứng bằng tích của chu vi đáy với chiều cao của nó.
Sxq = C . h
Trong đó Sxq: Diện tích xung quanh của hình lăng trụ,
C: Chu vi một đáy của hình lăng trụ,
h: chiều cao của lăng trụ.
• Thể tích của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác. Thể tích của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác.
V = Sday . h
Trong đó: V : Thể tích của hình lăng trụ đứng,
S : Diện tích một đáy của hình lăng trụ đứng,
h : Chiều cao của hình lăng trụ đứng.
c) Diện tích toàn phần (mở rộng):
Diện tích toàn phần bằng diện tích xung quanh cộng diện tích hai đáy.
Stp = Sxq + 2Sđ
Trong đó: Stp là diện tích toàn phần của hình lăng trụ.
Sxq: Diện tích xung quanh của hình lăng trụ.
5. Bài tập
Bài 1. Cho tam giác ABC, có góc A = 90º, d là đường thẳng qua C và vuông góc với BC; tia phân giác của góc B cắt AC ở D và cắt d ở E. Kẻ CH vuông góc với DE, H thuộc DE. Chứng minh CH là tia phân giác của góc DCE?
Bài 2: Cho tam giác ABC, góc B > góc C, AD là tia phân giác
a) Chứng minh góc ADC - ADB = góc B - C
b) Phân giác góc ngoài tại A của tam giác ABC cắt BC ở E. Chứng minh góc AEB = 1/2 (B -C)
Bài 3: Cho tam giác ABC, gọi D, E lần lượt là trung điểm của AC, AB. Trên tia đối của tia DB lấy M sao cho DM = DB; trên tia đối của tia EC lấy N sao cho EN = EC. Chứng minh A là trung điểm của MN?
Bài 4: Cho tam giác ABC có góc A = 50°. Vẽ đoạn thẳng AI vuông góc và bằng AB (I và C khác phía với AB). Vẽ đoạn thẳng AK vuong góc và bằng AC (K và B khác phía với AC). Chứng minh:
a) IC = BK
b) IC vuông góc BK
Bài 5: Cho tam giác ABC có tia phân giác của góc ABC cắt cạnh AC ở D, tia phân giác của góc ACB cắt cạnh AB ở E. Biết BE + CD = BC. Tính số đo góc BAC?
Bài 6: Cho tam giác ABC có góc B = 2C. Tia phân giác của góc B cắt AC ở D. Trên tia đối của BD lấy E sao cho BE = AC. Trên tia đối của CB lấy K sao cho CK = AB. Chứng minh AE = AK.
Bài 7: Cho tam giác ABC. Trên AB lấy D à E sao cho AD = BE. Qua D, E vẽ các đường thẳng song song với BC, chúng cắt AC theo thứ tự ở M và N. Chứng minh BC = DM + EN.
Bài 8: Cho tam giác ABC có góc A = 600. Các tia phân giác của các góc B và C cắt nhau ở I và cắt AC, AB theo thứ tự ở D và E. Chứng minh ID = IE.
Bài 9: Cho tam giác ABC vuông tại A có AB = AC. Lấy D thuộc AB, E thuộc AC sao cho AD = AE. Đường thẳng đi qua D vuông góc với BE cắt CA ở K. Chứng minh AK = AC?
Bài 10: Cho tam giác ABC có góc A nhọn. Trên nửa mặt phẳng bờ AB chứ C, vẽ AD vuông góc với AB, AD = AB. Trên nửa mặt phẳng bờ AC chứa B, vẽ AE vuông góc AC, AE = AC. Kẻ AH vuông góc ED tại H. Chứng minh AH đi qua trung điểm của BC?
Bài 11: Gọi D là trung điểm cạnh BC của tam giác ABC. Qua D kẻ đường thẳng vuông góc với đường phân giác trong của góc BAC cắt AB, AC lần lượt ở M và N.
a) Chứng minh BM = CN
b) Cho biết AB = c, AC = b. Tính độ dài các đoạn thẳng AM, BM.
Bài 12: Cho tam giác ABC vuông tại A. đường phân giác BE. Kẻ EH vuông góc với BC. gọi K là giao điểm của AB và HE. Chứng minh rằng:
a) Δ ABE = Δ HBE
b) BE là đường trung trực của AH.
c) EK = EC.
d) AE < EC
Bài 13: Cho tam giác ABC vuông tại A (AB < AC).Trên tia đối của tia AC lấy điểm D sao cho AD = AB. Trên tia đối của tia AB lấy điểm E sao cho AE = AC.
a) Chứng minh: BC = DE.
b) Chứng minh: tam giác ABD vuông cân và BD // CE.
c) Kẻ đường cao AH của tam giác ABC tia AH cắt cạnh DE tại M. từ A kẻ đường vuông góc CM tại K, đường thẳng này cắt BC tại N . Chứng minh: NM // AB.
d) Chứng minh: AM = DE/2.
Bài 14: Cho tam giác ABC vuông tại A có. Vẽ AK vuông góc BC (K thuộc BC). Trên tia đối của tia KA lấy điểm M sao cho KA = KM
a) Chứng minh: DKAB = DKMB. Tính số đo góc MAB
b) Trên tia KB lấy điểm D sao cho KD = KC. Tia MD cắt AB tại N. Chứng minh: MN vuông góc AB
c) So sánh MD + DB với AB
Bài 15: Cho tam giác ABC cân tại A. Trên tia đối của BC lấy điểm M , trên tia đối của CB lấy N sao cho BM = CN , Vẽ BD vuông góc AM tại D, CE vuông góc AN tại E. Cho biết AB = 10 cm, BH = 6 cm. Tính độ dài đoạn AH
a) Chứng minh: Tam giác AMN cân.
b) Chứng minh: DB = CE
c) Gọi K là giao điểm của DB và EC. Chứng minh ΔADK = ΔAEK.
d) Chứng minh KD + KE < 2KA .
Bài 16: Cho ΔABC vuông tại A có AB = 6cm; AC = 8cm. Vẽ trung tuyến AM.
a) Tính độ dài AM.
b) Trên tia đối của tia MA lấy điểm D sao cho MD = MA. Chứng minh: ΔAMB = ΔDMC
c) Chứng minh: AC vuông góc DC
d) Chứng minh: AM < (AB + AC ) : 2
Bài 17: Tam giác ABC vuông tại A; phân giác BD. Kẻ DE vuông góc BC (E thuộc BC). Gọi F là giao điểm của BA và ED. Chứng minh:
a) BD là đường trung trực của AE
b) DF = DC
c) AD < DC
Bài 18: Cho tam giác vuông tại A, đường trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a) Tính số đo góc ABD.
b) Chứng minh rằng tam giác ABC bằng tam giác BAD.
c) So sánh độ dài AM và BC.
Bài 19: Cạnh của một hình lập phương bằng 2 cm. Tính diện tích toàn phần và diện tích xung quanh của hình lập phương đó.
Bài 20: Cho hình chữ nhật có thể tích 144 cm3, diện tích xung quanh là 168 cm2, diện tích toàn phần là 192 cm2. Tính các kích thước của hình hộp chữ nhật đó.
Bài 21: Một căn phòng hình hộp chữ nhật có chiều dài 4,5 m, chiều rộng 4 m, chiều cao 3 m. Người ta muốn lăn sơn trần nhà và bốn bức tường. Biết rằng tổng diện tích các cửa là Tính diện tích cần lăn sơn?
Bài 22: Một tấm lịch để bàn có dạng một lăng trụ đứng, ACB là một tam giác cân tại C. Tính diện tích miếng bìa để làm một tấm lịch như trên.
Bài 23: Một lều trại có dạng hình lăng trụ đứng đáy là tam giác, thể tích phần không gian bên trong là 2,16 cm3. Biết chiều dài CC' của lều là 2,4 m, chiều rộng BC của lều là 1,2 m. Tính chiều cao AH của lều.
Bài 24: Cho hình lăng trụ đứng có đáy là hình thoi cạnh 6 cm và diện tích xung quanh của hình lăng trụ là 192 (cm2). Tính chiều cao của hình lăng trụ.



