Tam giác cân. Đường trung trực của đoạn thẳng lớp 7

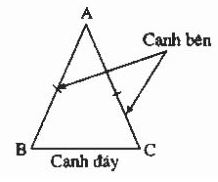
– Tam giác cân là tam giác có hai cạnh bằng nhau.

Ví dụ: Ta có tam giác cân ABC cân tại A (AB = AC). Ta gọi AB và AC là các cạnh bên, BC là cạnh đáy, ∠B và ∠C là các góc ở đáy, ∠A là góc ở đỉnh.

– Trong tam giác cân, hai góc ở đáy bằng nhau.

– Dấu hiệu nhận biết:

• Nếu một tam giác có hai cạnh bằng nhau thì tam giác đó là tam giác cân.

• Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.

– Định nghĩa tam giác vuông cân: Tam giác vuông cân là tam giác vuông có hai cạnh góc vuông bằng nhau.

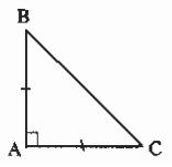
Ví dụ: ΔABC vuông cân tại A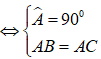

– Tính chất: Mỗi góc nhọn của tam giác vuông cân bằng 45^o

Ví dụ: ΔABC vuông cân tại A ⇒ ∠B = ∠C = 45^o.

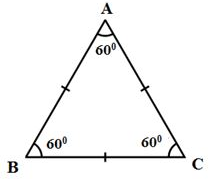
– Định nghĩa: Tam giác đều là tam giác có ba cạnh bằng nhau:

ΔABC đều ⇔ AB = BC = AC

– Tính chất: Trong tam giác đều, mỗi góc bằng 60^o: ΔABC đều ⇔ ∠A = ∠B = ∠C = 60^o

– Dấu hiệu nhận biết:

• Nếu tam giác có ba cạnh bằng nhau thì tam giác đó là tam giác đều.

• Nếu tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều.

• Nếu một tam giác cân có một góc nhọn bằng 60^o thì tam giác đó là tam giác đều.

– Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó.

– Tính chất: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.

– Nhận xét: Điểm cách đều hai mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.

MA = MB ⇒ M thuộc đường trung trực của AB

– Tập hợp các điểm cách đều hai mút của một đoạn thẳng là đường trung trực của đoạn thẳng đó.

 Tải file để xem thêm bài tập và đáp án chi tiết