Tính chất ba đường trung trực của tam giác
Chuyên đề Toán học lớp 7: Tính chất ba đường trung trực của tam giác được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 7 hiệu quả hơn. Mời các bạn tham khảo.
Chuyên đề: Tính chất ba đường trung trực của tam giác
A. Lý thuyết
1. Đường trung trực của tam giác
• Trong một tam giác, đường trung trực của mỗi cạnh gọi là đường trung trực của tam giác đó.
Ví dụ: a là đường trung trực ứng với cạnh BC của tam giác ABC.
• Mỗi tam giác có ba đường trung trực.
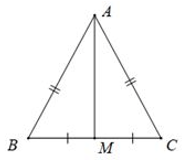
Tính chất: Trong một tam giác cân, đường trung trực của cạnh đáy đồng thời là đường trung tuyến ứng với cạnh này.
2. Tính chất ba đường trung trực của tam giác
•Ba đường trung trực của một tam giác cùng đi qua một điểm. Điểm này cách đều ba đỉnh của tam giác đó.
•Điểm O là giao điểm ba đường trung trực của tam giác ABC, ta có OA = OB = OC
Chú ý: Vì giao điểm O của ba đường trung trực của tam giác ABC cách đều ba đỉnh của tam giác đó nên có một đường tròn tâm O đi qua ba đỉnh A, B, C. Ta gọi đường tròn đó là đường tròn ngoại tiếp tam giác ABC.

B. Trắc nghiệm & Tự luận
I. Câu hỏi trắc nghiệm
Bài 1: Cho Δ ABC, hai đường cao BD và CE. Gọi M là trung điểm của BC. Em hãy chọn câu sai:
A. BM = MC
B. ME = MD
C. DM = MB
D. M không thuộc đường trung trực của DE
Giải:
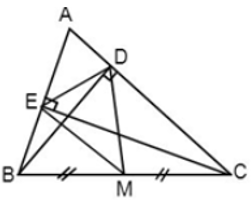
Vì M là trung điểm của BC (gt) suy ra BM = MC (tính chất trung điểm), loại đáp án A.
Xét Δ BCE có M là trung điểm của BC (gt) suy ra EM là trung tuyến
⇒ EM = BC/2 (1) (trong tam giác vuông đường trung tuyến ứng cới cạnh huyền bằng nửa cạnh ấy)
Xét Δ BCD có M là trung điểm của BC (gt) suy ra DM là trung tuyến
⇒ DM = MB = BC/2 (2) (trong tam giác vuông đường trung tuyến ứng cới cạnh huyền bằng nửa cạnh ấy) nên loại đáp án C
Từ (1) và (2) ⇒ EM = DM ⇒ M thuộc đường trung trực của DE. Loại đáp án B, chọn đáp án D
Chọn đáp án D
Bài 2: Cho Δ ABC có AC > AB. Trên cạnh AC lấy điểm E sao cho CE = AB. Các đường trung trực của BE và AC cắt nhau tại O. Chọn câu đúng
A. Δ ABO = Δ COE
B. Δ BOA = Δ COE
C. Δ AOB = Δ COE
D. Δ ABO = Δ CEO

+ OA = OC (vì O thuộc đường trung trực của AC )
+ OB = OE (vì O thuộc đường trung trực của BE )
+ AB = CE (giả thiết)
Do đó Δ AOB = Δ COE (c-c-c)
Chọn đáp án C
Bài 3: Cho Δ ABC có AC > AB. Trên cạnh AC lấy điểm E sao cho CE = AB. Các đường trung trực của BE và AC cắt nhau tại O. Chọn câu đúng
A. AO là đường trung tuyến của tam giác ABC
B. AO là đường trung trực của tam giác ABC
C. AO ⊥ BC
D. AO là tia phân giác của góc A
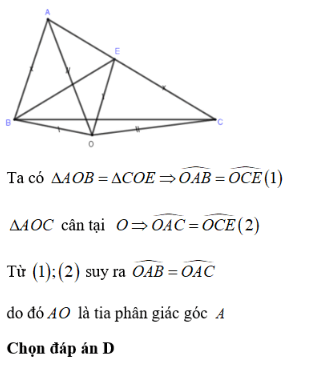
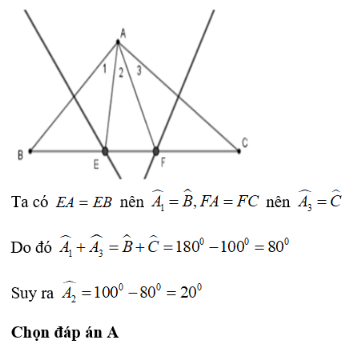
Bài 4: Cho Δ ABC trong đó ∠A = 100°. Các đường trung trực của AB và AC cắt cạnh BC theo thứ tự tại E và F. Tính ∠EAF .
A. 20°
B. 30°
C. 40°
D. 50°
Bài 5: Cho Δ ABC vuông tại A, kẻ đường cao AH. Trên cạnh AC lấy điểm K sao cho AK = AH. Kẻ KD ⊥ AC (D ∈ BC) . Chọn câu đúng
A. Δ AHD = Δ AKD
B. AD là đường trung trực của đoạn thẳng HK
C. AD là tia phân giác của góc HAK
D. Cả A, B, C đều đúng
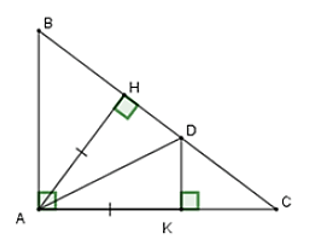
Xét tam giác vuông AHD và tam giác vuông AKD có:
+ AH = AK (gt)
+ AD chung
Suy ra Δ AHD = Δ AKD (ch-cgv) nên A đúng
Từ đó ta có HD = DK; ∠HAD = ∠DAK suy ra AD là tia phân giác của góc HAK nên C đúng
Ta có AH = AK (gt) và HA = DK (cmt) suy ra AD là đường trung trực của đoạn thẳng HK nên B đúng
Vậy A, B, C đều đúng
Chọn đáp án D
II. Bài tập tự luận
Bài 1: Cho tam giác ABC có đường phân giác AK của góc A. Biết rằng giao điểm của đường phân giác của tam giác ABK trùng với giao điểm ba đường trung trực của tam giác ABC. Tìm số đo các góc của tam giác ABC.
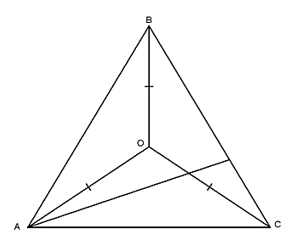
Gọi O là giao điểm của 3 đường phân giác của tam giác ABK
Theo đề bài, O là giao điểm của ba đường trung trực của tam giác ABC
Vậy OA = OB = OC và các tam giác AOB, AOC, BOC đều là các tam giác đều tại đỉnh O
Gọi![]()
Vì AK là đường phân giác của góc BAC nên nếu ∠KAB = 2a thì ∠BAC = 4a
Ta có: ΔAOB = ΔCOB ⇒ AB = CB
Vậy tam giác ABC cân tại đỉnh B
⇒ ∠BAC = ∠ BCA
Khi đó ta có:
2a + 4a + 4a = 180° ⇒ 10a = 180° ⇒ a = 18°
Vậy số đo cách góc của tam giác ABC là ∠A = ∠C = 72°, ∠B = 36°
Bài 2: Trên ba cạnh AB, BC và CA của tam giác đều ABC, lấy các điểm theo thứ tự M, N, P sao cho AM = BN = CP. Gọi O là giao điểm của ba đường trung trực của tam giác ABC. Chứng minh O cũng là gia điểm của ba đường trung trực của tam giác MNP.
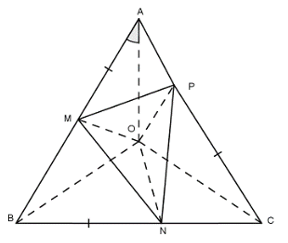
Theo giả thiết O là giao điểm của ba đường trung trực của tam giác ABC nên ta có: OA = OB = OC.
⇒ Các tam giác AOM, BON, COP có:
AM = BN = CP (gt)
![]() (vì ABC là tam giác đều nên đường trung trực cũng là đường phân giác)
(vì ABC là tam giác đều nên đường trung trực cũng là đường phân giác)
OA = OB = OC
Do đó: ΔAOM = ΔBON = ΔCOP (c-g-c)
⇒ OM = ON = OP
Hay O là giao điểm của ba đường trung trực tam giác MNP
Bài 3: Cho tam giác ABC có ba góc nhọn, O là giao điểm hai đường trung trực của AB và AC. Trên tia đối của tia OB lấy điểm D sao cho OB = OD.
a) Chứng minh O thuộc đường trung trực của AD và CD .
b) Chứng minh các tam giác ABD và CBD vuông.
c) Biết góc ABC = 70o. Hãy tính số đo góc ADC.
Bài 4: Tam giác ABC có ba đường trung tuyến cắt nhau tại O. Biết rằng điểm O cũng là giao điểm của ba đường trung trực trong tam giác ABC. Chứng minh tam giác ABC đều.
Bài 5: Cho tam giác ABC đều. Trên cạnh AB, BC,CA lấy theo thứ tự ba điểm M, N, P sao cho
AM = BN = CP
a. Chứng minh tam giác MNP là tam giác đều
b. Gọi O là giao điểm các đường trung trực của tam giác ABC.
Chứng minh rằng điểm O cũng là giao điểm các đường trung trực của tam giác MNP







