Giá trị của một biểu thức đại số

Chuyên đề Toán học lớp 7: Giá trị của một biểu thức đại số được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu bao gồm lý thuyết cơ bản kèm bài tập vận dụng sẽ giúp các bạn học sinh học tốt môn Toán học lớp 7 hiệu quả hơn. Mời các bạn tham khảo.

A. Lý thuyết Giá trị của một biểu thức đại số

1. Giá trị của một biểu thức đại số

Ví dụ: Tính giá trị của biểu thức x²y³ + xy tại x = 1 và y = 1/2

Ta thay x = 1 và y = 1/2 vào biểu thức x²y³ + xy

Ta có:  \(1^2.\left(\frac{1}{2}\right)^3+1.\frac{1}{2}=\frac{5}{8}\)

Vậy giá trị của biểu thức đã cho tại x = 1 và y = 1/2 là 5/8.

2. Lưu ý

2. Các dạng toán thường gặp

2.1. Dạng 1: Tính giá trị của biểu thức đại số

2.2. Dạng 2: Tính giá trị của biểu thức khi biết mối quan hệ giữa các biến

2.3. Dạng 3: Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức

B. Trắc nghiệm & Tự luận

I. Câu hỏi trắc nghiệm

Bài 1: Giá trị của biểu thức x³ + 2x² − 3 tại x = 2 là

A. 13

B. 10

C. 19

D. 9

Lời giải: Thay x = 2 vào biểu thức x³ + 2x² − 3 ta được

2³ + 2.2² − 3 = 8 + 8 − 3 = 13

Chọn đáp án A

Bài 2: Cho biểu thức đại số A = x² − 3x + 8. Giá trị của A tại x = − 2 là:

A. 13

B. 18

C. 19

D. 9

Lời giải: Thay vào biểu thức ta có:

(− 2)² − 3.(− 2) + 8 = 4 + 6 + 8 = 18

Vậy A = 18 tại x = − 2

Chọn đáp án B

Bài 3: Cho biểu thức đại số B = x³ + 6x − 35. Giá trị của B tại x = 3, y = − 4 là:

A. 16

B. 86

C. − 32

D. − 28

Lời giải: Thay x = 3, y = − 4 vào biểu thức B để tìm giá trị của biểu thức B ta có:

3³ + 6.(− 4) − 35 = 27 − 24 − 35 = 3 − 35 = − 32

Vậy B = − 32 tại x = 3, y = − 4

Chọn đáp án C

Bài 4: Cho A = 4x²y − 5 và B = 3x²y + 6 x²y² + 3xy². So sánh A và B khi x = − 1, y = 3

A. A > B

B. A = B

C. A < B

D. A ≥ B

Lời giải: + Thay x = − 1, y = 3 vào biểu thức A ta được

A = 4.(− 1)².3 − 5 = 7

+ Thay x = − 1, y = 3 vào biểu thức B ta được

B = 3.(−1)² + 6.(− 1)².3² + 3.(− 1).3² = − 9 + 54 − 27 = 18

Suy ra A < B khi x = − 1, y = 3

Chọn đáp án C

Bài 5: Tính giá trị biểu thức B = 5x² − 2x − 18 tại |x| = 4

A. B = 54

B. B = 70

C. B = 54 hoặc B = 70

D. B = 45 hoặc B = 70

Lời giải:

Ta có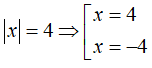

+ Trường hợp 1: x = 4 : Thay x = 4 vào biểu thức ta có:

5.4² − 2.4 − 18 = 5.16 − 8 − 18 = 80 − 8 − 18 = 54

Vậy B = 54 tại x = 4

+ Trường hợp 2: x = − 4 : Thay x = − 4 vào biểu thức ta có:

5.(− 4)² − 2.(− 4) − 18 = 5.16 + 8 − 18 = 80 + 8 − 18 = 70

Vậy B = 70 tại x = − 4

Với |x| = 4 thì B = 54 hoặc B = 70

Chọn đáp án C

II. Bài tập tự luận

Bài 1: Tính giá trị của biểu thức x³ − 2x + 1 tại x = 1, x = − 2, x = 1/2

Đáp án

Giá trị của biểu thức x³ − 2x + 1 tại x = 1 là:

1³ − 2.1 + 1 = 0

Giá trị của biểu thức x³ − 2x + 1 tại x = − 2 là:

(− 2)² − 2.(− 3) + 1 = − 1

Giá trị của biểu thức x³ − 2x + 1 tại \(x=\frac{1}{2}\) là:

\(\left(\frac{1}{3}\right)^3 -2.\frac{1}{2} +1=\frac{1}{8}\)

Bài 2:

a) Tính giá trị của biểu thức \(\frac{x+y^2}{5}+xy\) tại x = 1, y = 3

b) Tính giá trị của biểu thức x⁵y² + 2y² tại x = 1, y = 2

Đáp án

a) Tính giá trị của biểu thức \(\frac{x+y^2}{5}+xy\) tại x = 1, y = 3 là:

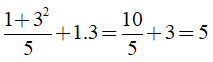
b) Tính giá trị của biểu thức x⁵y² + 2y² tại x = 1, y = 2 là:

1⁵ . 2² + 2 . 2² = 4 + 8 = 12

Bài 3: Tính giá trị của biểu thức A = x² + 4xy - 3y³ với |x| = 5; |y| = 1.

Bài 4: Tính giá trị biểu thức sau biết x + y = 0.

a) A = 2x + 2y + 3xy(x + y) + 5(x³y² + x²y³) + 4.

b) B = 3xy(x + y) + 2x³y² + 2x²y³ + 5