Quan hệ giữa ba cạnh của một tam giác - Bất đẳng thức tam giác
Chuyên đề Toán học lớp 7: Quan hệ giữa ba cạnh của một tam giác - Bất đẳng thức tam giác được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 7 hiệu quả hơn. Mời các bạn tham khảo.
Chuyên đề: Quan hệ giữa ba cạnh của một tam giác - Bất đẳng thức tam giác
A. Lý thuyết
1. Bất đẳng thức tam giác
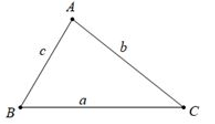
Trong một tam giác, độ dài của một cạnh bất kỳ luôn nhỏ hơn tổng độ dài hai cạnh còn lại.
Cho tam giác ABC, ta có các bất đẳng thức sau:
• AB < AC + BC hay c < a + b
• AC < AB + BC hay b < a + c
• BC < AB + AC hay a < b + c
2. Hệ quả của bất đẳng thức tam giác
– Trong một tam giác, độ dài của một cạnh bất kỳ luôn lớn hơn hiệu độ dài hai cạnh còn lại.
– Nhận xét: Nếu xét đồng thời cả tổng và hiệu độ dài hai cạnh của một tam giác thì quan hệ giữa các cạnh của nó còn được phát biểu như sau:
Trong một tam giác, độ dài một cạnh bao giờ cũng lớn hơn hiệu và nhỏ hơn tổng các độ dài của hai cạnh còn lại.
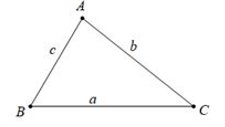
Ví dụ: Trong tam giác ABC, với cạnh BC ta có:
|AC – AB| < BC < AC + AB hay |b – c| < a < b + c
B. Trắc nghiệm & Tự luận
I. Câu hỏi trắc nghiệm
Bài 1: Cho ΔABC, chọn đáp án sai trong các đáp án sau:
A. AB + BC > AC
B. BC - AB < AC
C. BC - AB < AC < BC + AB
D. AB - AC > BC
Lời giải: Vì trong một tam giác tổng độ dài hai cạnh bất kì lớn hơn độ dài cạnh còn lại và hiệu độ dài hai cạnh bất kì nhỏ hơn độ dài cạnh còn lại nên các đáp án A, B, C đúng và D sai.
Chọn đáp án D.
Bài 2: Dựa vào bất đẳng thức tam giác, kiểm tra xem bộ ba nào trong các bộ ba đoạn thẳng có độ dài sau đây không thể là ba cạnh của một tam giác:
A. 3 cm, 5 cm, 7 cm
B. 4 cm, 5 cm, 6 cm
C. 2 cm, 5 cm, 7 cm
D. 3 cm, 6 cm, 5 cm
Lời giải: • Xét bộ ba: 3 cm, 5 cm, 7 cm .
Ta có:
(thỏa mãn bất đẳng thức tam giác) nên bộ ba 3 cm, 5 cm, 7 cm lập thành một tam giác nên loại A.
• Xét bộ ba: 4 cm, 5 cm, 6 cm
Ta có: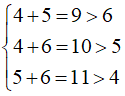
(thỏa mãn bất đẳng thức tam giác) nên bộ ba 4cm, 5cm, 6cm lập thành một tam giác nên loại A.
• Xét bộ ba: 3 cm, 6 cm, 5 cm
Ta có:
(thỏa mãn bất đẳng thức tam giác) nên bộ ba 3cm, 6cm, 5cm lập thành một tam giác nên loại A.
• Xét bộ ba: 2 cm, 5 cm, 7 cm . Ta có: 2 + 5 = 7 (không thỏa mãn bất đẳng thức tam giác) nên bộ ba 2 cm, 5 cm, 7 cm không lập thành một tam giác nên chọn C.
Chọn đáp án C.
Bài 3: Cho ΔABC có cạnh AB = 1cm và BC = 4cm. Tính độ dài cạnh AC biết độ dài cạnh AC là một số nguyên:
A. 1 cm
B. 2 cm
C. 3 cm
D. 4 cm
Lời giải: Gọi độ dài cạnh AC là x (x > 0).
Theo bất đẳng thức tam giác ta có:
4 - 1 < x < 4 + 1
⇔ 3 < x < 5
Vì x là số nguyên nên x = 4.
Vậy độ dài cạnh AC = 4 cm
Chọn đáp án D.
Bài 4: Cho tam giác ABC biết AB = 1 cm, BC = 9 cm và cạnh AC là một số nguyên. Chu vi tam giác ABC là:
A. 17 cm
B. 18 cm
C. 19 cm
D. 16 cm
Lời giải: Gọi độ dài cạnh AC là x (x > 0).
Theo bất đẳng thức tam giác ta có:
9 - 1 < x < 9 + 1
⇔ 8 < x < 10
Vì x là số nguyên nên x = 9.
Vậy độ dài cạnh AC = 9 cm
Chu vi tam giác là: AB + BC + AC = 1 + 9 + 9 = 19 cm
Chọn đáp án C.
Bài 5: Cho tam giác ABC có BC = 1 cm, AC = 8 cm và độ dài cạnh AB là một số nguyên (cm). Tam giác ABC là tam giác gì?
A. Tam giác vuông tại A
B. Tam giác cân tại A
C. Tam giác vuông cân tại A
D. Tam giác cân tại B
Lời giải: Gọi độ dài cạnh AB là x (x > 0).
Theo bất đẳng thức tam giác ta có:
8 - 1 < x < 8 + 1
⇔ 7 < x < 9
Vì x là số nguyên nên x = 8.
Vậy độ dài cạnh AB = 8 cm
Tam giác ABC có AB = AC = 8 cm nên tam giác ABC cân tại A.
Chọn đáp án B.
II. Bài tập tự luận
Bài 1: Hãy tìm độ dài các cạnh của một tam giác, biết cạnh thứ nhất gấp rưỡi cạnh thứ hai, cạnh thứ hai gấp rưỡi cạnh thứ ba và nửa chu vi tam giác bằng 9,5 cm
Gọi độ dài cạnh thứ ba là x (cm)
Theo độ dài, độ dài cạnh thứ hai là (3/2)x (cm)
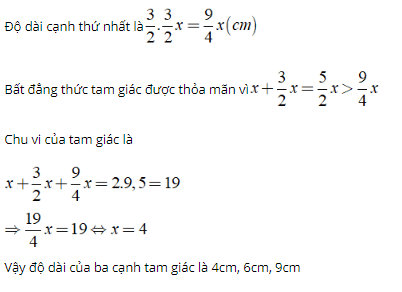
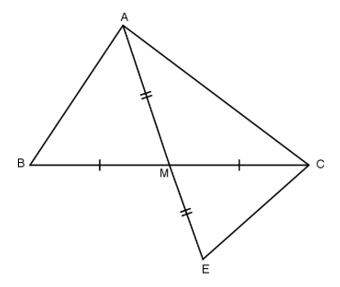
Bài 2: Cho tam giác ABC có AC > AB. Nối A với trung điểm M của BC. Trên tia AM lấy điểm E sao cho M là trung điểm của đoạn AE. Nối C với E.
a) So sánh hai đoạn thẳng AB và CE.
b) Chứng minh: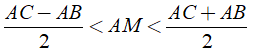
Bài 3: Độ dài hai cạnh của một tam giác bằng 6 cm và 2 cm. Tính độ dài cạnh còn lại biết rằng số đo của cạnh đó theo cm là một số tự nhiên chẵn.
Bài 4: Tính chu vi của tam giác cân có hai cạnh bằng 4 m và 8 m.
Bài 5: Có bao nhiêu tam giác có độ dài hai cạnh là 7 cm và 2 cm còn độ dài cạnh thứ ba là một số nguyên (đơn vị cm)?
