Tính chất ba đường trung tuyến của tam giác
Chuyên đề Toán học lớp 7: Tính chất ba đường trung tuyến của tam giác được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 7 hiệu quả hơn. Mời các bạn tham khảo.
Chuyên đề: Tính chất ba đường trung tuyến của tam giác
A. Lý thuyết
1. Đường thẳng trung tuyến của tam giác
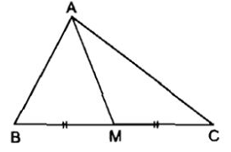
• Đoạn thẳng AM nối đỉnh A của tam giác ABC với trung điểm M của cạnh BC gọi là đường trung tuyến (xuất phát từ đỉnh A hoặc ứng với cạnh BC) của tam giác ABC.
• Đường thẳng AM cũng gọi là đường trung tuyến của tam giác ABC.
• Mỗi tam giác có ba đường trung tuyến.
2. Tính chất ba đường trung tuyến của tam giác
• Định lý 1: Ba đường trung tuyến của một tam giác cùng đi qua một điểm(hay đồng quy tại một điểm). Điểm gặp nhau của ba đường trung tuyến gọi là trọng tâm của tam giác đó.
• Định lý 2: Vị trí trọng tâm: Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy.
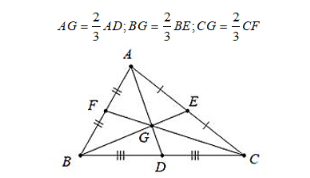
Ví dụ: Với G là trọng tâm của ΔABC ta có:
B. Trắc nghiệm & Tự luận
I. Câu hỏi trắc nghiệm
Bài 1: Chọn câu sai:
A. Trong một tam giác có ba đường trung tuyến
B. Các đường trung tuyến của tam giác cắt tại một điểm
C. Giao của ba đường trung tuyến của một tam giác gọi là trọng tâm của tam giác đó
D. Một tam giác có hai trọng tâm
Lời giải: Một tam giác chỉ có một trọng tâm nên D sai.
Chọn đáp án D.
Bài 2: Điền số thích hợp vào chỗ trống: “Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng … độ dài đường trung tuyến đi qua đỉnh ấy”
A. 2/3
B. 3/2
C. 3
D. 2
Lời giải: Định lý: Vị trí trọng tâm: Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy
Số cần điền là 2/3.
Chọn đáp án A.
Bài 3: Cho hình vẽ sau:
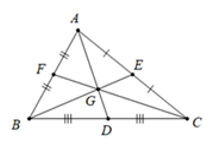
Điền số thích hợp vào chỗ chấm: BG = .... BE
A. 2
B. 3
C. 1/3
D. 2/3
Lời giải: Ta có AD, BE, CF là ba đường trung tuyến của tam giác ABC và chúng cắt nhau tại G nên G là trọng tâm của tam giác ABC.
Theo tính chất ba đường trung tuyến của tam giác ta có:
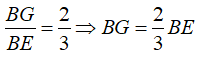
Vậy số thích hợp điền vào chỗ chấm là: 2/3
Chọn đáp án D.
Bài 4: Cho hình vẽ sau:

Điền số thích hợp vào chỗ chấm: AG = .... GD
A. 2
B. 3
C. 1/3
D. 2/3
Lời giải: Ta có AD, BE, CF là ba đường trung tuyến của tam giác ABC và chúng cắt nhau tại G nên G là trọng tâm của tam giác ABC .
Theo tính chất ba đường trung tuyến của tam giác ta có:
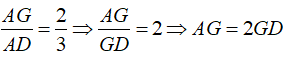
Vậy số thích hợp điền vào chỗ chấm là: 2
Chọn đáp án A.
Bài 5: Tam giác ABC có trung tuyến AM = 9 cm và trọng tâm G. Độ dài đoạn AG là:
A. 4,5 cm
B. 3 cm
C. 6 cm
D. 4 cm
Lời giải: Vì G là trọng tâm của tam giác ABC và AM là đường trung tuyến nên AG = (2/3)AM (tính chất ba đường trung tuyến của tam giác)
Do đó: AG = (2/3).9 = 6 cm
Chọn đáp án C.
II. Bài tập tự luận
Bài 1: Cho hai đường thẳng xx' và yy' cắt nhau tại O. Trên tia Ox lấy hai điểm A, B sao cho A nằm giữa O và B, AB = 2OA. Trên yy' lấy hai điểm L và M sao cho O là trung điểm của LM. Nối B với L, B với M và gọi P là trung điểm của đoạn MB, Q là trung điểm của đoạn LB. Chứng minh rằng các đoạn thẳng LP và MQ đi qua A.
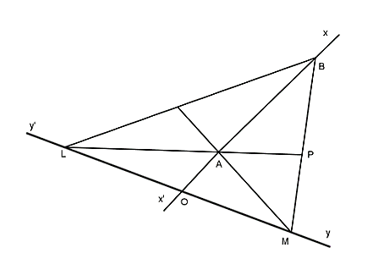
Ta có O là trung điểm của đoạn LM
Suy ra BO là đường trung tuyến của ΔBLM (1)
Mặt khác BO = BA + AO vì A nằm giữa O và B hay OB = 2OA + OA = 3OA
Suy ra AO = (1/3)OB hay BA = (2/3)BO (2)
Từ (1) (2) suy ra A là trọng tâm của ΔBLM (tính chất trọng tâm)
Mà LP và MQ là các đường trung tuyến của ΔBLM vì P là trung điểm MB và O là trung điểm của đoạn LB
Suy ra các đoạn thẳng LP và MQ đi qua A (theo tính chất 3 đường trung tuyến)
Bài 2: Cho ΔABC, BC = a, CA = b, AB = c. Kẻ trung tuyến AM. Đặt AM = ma. Chứng minh rằng
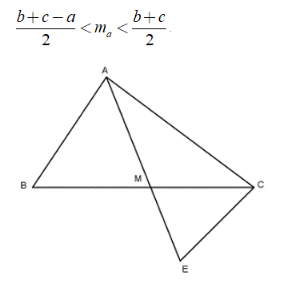
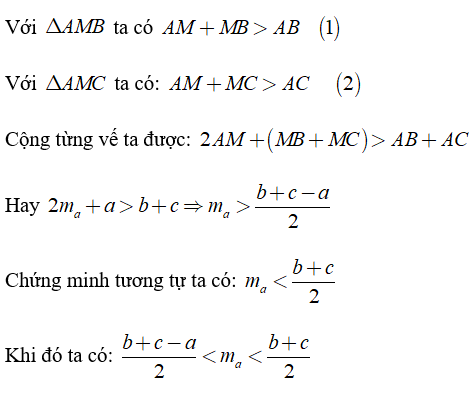
Bài 3: Cho tam giác ABC có hai đường trung tuyến BP, CQ cắt nhau tại G. Trên tia đối của tia PB lấy điểm E sao cho PE = PG. Trên tia đối của tia QG lấy điểm F sao cho QF = QG. Chứng minh:
a) GB = GE, GC = GE
b) EF = BC và EF // BC.
Bài 4: Cho tam giác ABC có hai đường trung tuyến AD, BE cắt nhau tại G. Trên tia đối của tia DG lấy điểm M sao cho D là trung điểm của đoạn thẳng MG. Trên tia đối của tia EG, lấy điểm N sao cho E là trung điểm GN. Chứng minh:
a) GN = GB, GM = GA
b) AN = MB và AN // MB
Bài 5: Cho Δ ABC với đường trung tuyến AD. Trên tia AD lấy điểm E sao cho AD = DE, trên tia BC lấy điểm M sao cho BC = CM. Chứng minh C là trọng tâm của Δ AEM.







